Достаточный признак выпуклости, вогнутости графика функции. Точки перегиба

График функции 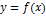называется выпуклымна интервале 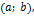если он расположен ниже любой своей касательной на этом интервале.

График функции 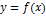называется вогнутымна интервале 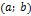, если он расположен выше любой своей касательной на этом интервале.

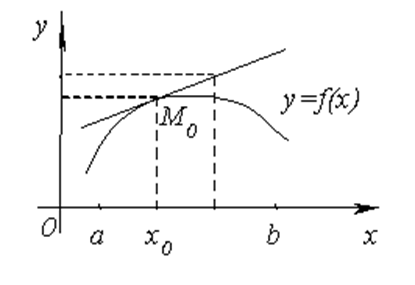
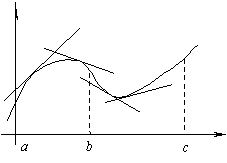На рисунке показана кривая, выпуклая на 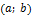и вогнутая на .

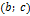Теорема. Пусть 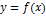дифференцируема на 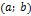. Если во всех точках интервала 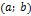вторая производная функции 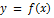отрицательная, т.е. 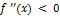, то график функции на этом интервале выпуклый, если же 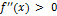– вогнутый.

Доказательство. Предположим для определенности, что 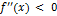и докажем, что график функции будет выпуклым.

Возьмем на графике функции 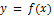произвольную точку M₀ с абсциссой 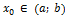и проведем через точку M₀ касательную. Ее уравнение 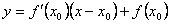. Мы должны показать, что график функции на 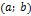лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой 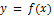будет меньше ордината касательной.

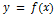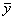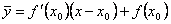Итак, уравнение кривой имеет вид . Обозначим ординату касательной, соответствующую абсциссе . Тогда . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет .

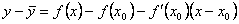Разность 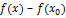преобразуем по теореме Лагранжа 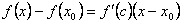, где c между x и x₀.

Таким образом,

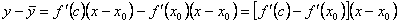
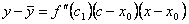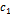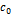К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: , где между и 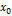. По условию теоремы 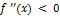. Определим знак произведения второго и третьего сомножителей.

1. Предположим, что 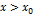. Тогда 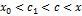, следовательно, 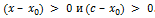Поэтому .

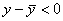2. Пусть 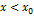, следовательно, 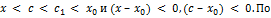этому вновь .

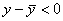Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях и 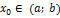, а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.

Теорема. Пусть кривая определяется уравнением 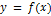. Если 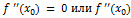не существует и при переходе через значение 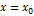производная 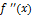меняет знак, то точка графика функции с абсциссой 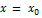есть точка перегиба.

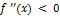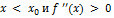Доказательство. Пусть при при 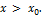Тогда при 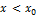кривая выпукла, а при 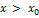– вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой 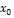есть точка перегиба. Аналогично можно рассматривать второй случай, когда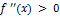 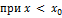ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> .

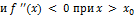Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.

Билет №33

Асимптоты графика функции. Общая схема исследования функции и построения графика

Прямая называется асимптотой графика функции 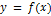, если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.

ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ

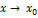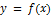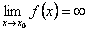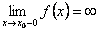Пусть при с какой-либо стороны функция неограниченно возрастает по абсолютной величине, т.е. или или 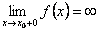. Тогда из определения асимптоты следует, что прямая 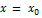является асимптотой. 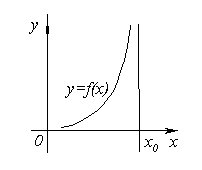Очевидно и обратное, если прямая 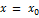является асимптотой, т. о. .

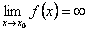Таким образом, вертикальной асимптотой графика функции 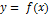называется прямая, если 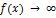хотя бы при одном из условий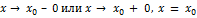

Следовательно, для отыскания вертикальных асимптот графика функции 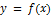нужно найти те значения 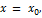при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение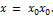

НАКЛОННЫЕ АСИМПТОТЫ

Поскольку асимптота – это прямая, то если кривая 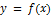имеет наклонную асимптоту, то ее уравнение будет 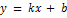. Наша задача найти коэффициенты k и 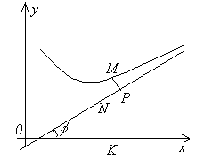b.

Теорема. Прямая 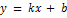служит наклонной асимптотой при 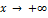для графика функции 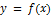тогда и только тогда, когда 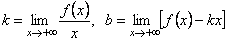. Аналогичное утверждение верно и при