Связь между дифференцируемостью и непрерывностью функции

1. Из непрерывности функции не следует ее дифференцируемость.

2. Из дифференцируемости функции следует ее непрерывность.

Найдем производную следующей функции . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

Покажем, что в точке нуль производная не существует. Для этого найдем производную в нуле по определению производной:

Данный предел равен 1, если и равен (-1), если , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.

Билет №21

Дифференциал функции одной переменной, его геометрический смысл, свойства

Функция y=f(x), определенная в точке А, называется дифференцируемой в точке х, принадлежащей А, если в некоторой окрестности этой точки приращение функции ∆f можно представить в виде ∆f = c∆x+α(∆x) ∆x, где с – постоянная, а α(∆x) – бесконечно малая величина.

Величина с∆x является главным членом разложения ∆y и называется дифференциалом функции. f(x) : df = c∆x. Геометрический смысл.

M''

M'

P

M

x

x+∆x

x

x+∆x

y(x)

Сравним ∆MM'P и ∆MM''P, где M' лежит на кривой, а M'' на касательной. Очевидно, что M'P=∆f, а M''P=tgӨ∆x=f'(x)∆x=df. Отсюда следует, что дифференциал численно равен приращению ординаты к касательной, проведенной к графику функций в точке х.

Билет №22

Применение дифференциала функции одной переменной для приближенных вычислений. Дифференциалы высших порядков

1) Δy ≈ y’ Δx = dy – дифференциал функции.

y(x₀ + Δx) – y(x₀) = y’Δx

y(x₀ + x) = y(x₀) = y(x₀) + y’(x₀) (1)

По формуле (1), зная значение , y(x₀), y’(x₀) можно определить y(x₀ + Δx).

2) Рассмотрим функцию 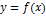. Дифференциал этой функции зависит от и , причем не зависит от , так как приращение в данной точке можно выбирать независимо от . В этом случае в формуле первого дифференциала будет постоянным. Тогда выражение зависит только от и его можно дифференцировать по .

Дифференциал от дифференциала функции в данной точке называется дифференциалом второго порядка или вторым дифференциалом.

Аналогично: .

Найдем формулу для вычисления второго дифференциала

т.е.

Аналогично получаем

Можно установить справедливость формулы

r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

Отсюда получаем

В частности, при n=1,2,3...

При этом предполагалось. что - независимая переменная.

Пусть теперь . Тогда .

Поэтому при вычислении будем считать его как дифференциал от произведения двух функций

Итак,

Для дифференциала третьего порядка имеет место формула

Из полученных формул следует, что при вычислении дифференциалов более высоких порядков от сложной функции происходит нарушение инвариантности формы.

Билет №23