Односторонние пределы. Необходимые и достаточные условия существования предела. Геометрический смысл предела.
Билет №1
Множества, способы их задания. Операции над множествами (объединение, пересечение).
Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку.
Множества могут быть конечными, бесконечными и пустыми.
Множества могут быть заданы списком, порождающей процедурой, арифметическими операциями, описанием свойств элементов или графическим представлением.
1. Задание множеств списком предполагает перечисление элементов. Например, множество  состоит из букв
состоит из букв 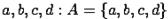 или множество
или множество 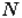 включает цифры
включает цифры 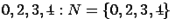 .
.
2. Задание множеств порождающей процедурой или арифметическими операциями означает описание характеристических свойств элементов множества: 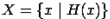 , т. е. множество
, т. е. множество 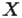 содержит такие элементы
содержит такие элементы 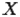 , которые обладают свойством
, которые обладают свойством 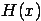 .
.
o 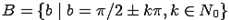 ,
, 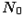 - множество всех натуральных чисел;
- множество всех натуральных чисел;
o 
3. Задание множества описанием свойств элементов: например, 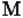 - это множество чисел, являющихся степенями двойки.
- это множество чисел, являющихся степенями двойки.
4. Графическое задание множеств происходит с помощью диаграмм Эйлера-Венна. Замкнутая линия-круг Эйлера - ограничивает множество, а рамка - универсальное пространство 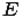 . Заданы два множества:
. Заданы два множества: 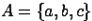 и
и 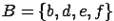 . Если элементов множеств немного, то они могут на диаграмме указываться явно.
. Если элементов множеств немного, то они могут на диаграмме указываться явно.
 Объединением множеств
Объединением множеств  и
и 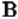 (
( 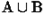 ) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств
) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств  или
или 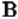 . Даны два множества:
. Даны два множества: 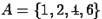 и
и 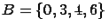 . Найдем множество
. Найдем множество 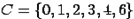 .
.
Пересечением множеств  и
и 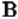 (
(  ) называется множество, состоящее из элементов, входящих как в множество
) называется множество, состоящее из элементов, входящих как в множество  , так и в множество
, так и в множество 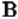 :
: 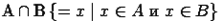 . Даны множества
. Даны множества 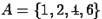 и
и 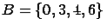 . Найдем их пересечение:
. Найдем их пересечение: 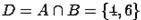 .
.
Билет №2
Функции, способы их задания, классификация.
Пусть даны 2 непустых множества A={x ∣x ∈ A}, B={y ∣y ∈ B} пусть f - некоторое отношение между А и В, если пара (х, у) является элементом отношения f, то говорят, что элементу у соответствует элемент х или элементу х сопоставляется элемент у.
Отношение fмежду А и В, при котором каждому элементу из А соответствует не более одного элемента из Вназывается функцией.
Различают 4 способа задания функции:
| х | х1 | х2 | х3 | х4 |
| у | у1 | у2 | у3 | у4 |
1. Табличный. Указывается значение аргумента x и соответствующе значение функции y=f(x).
2. Аналитический. Является наиболее важным для МА (мат. анализа), поскольку методы МА (дифференциального, интегрального счисления) предполагают этот способ задания. Одна и та же функция может быть задана различными формулами: y=∣sin(x)∣y=√1−cos2(x).
3. Графический. Область определения -- проекция данного графика на Ох, а множество значений -- проекция Д(f) на Оу.
4. Словестный. Например, y=[x] : x из R (Целой частью х из R называют любое целое число не превосходящее х).
Имеет место следующая классификация функций:
1) Функция вида Pn (x)=a0xn + a1xn-1 + a2xn-2 + … + an, где n ∊ N∪{0}, a0, a1, …, an ∊ R, называется целой рациональной функцией или многочленом степени n.
2) Функция, представляющая собой отношение двух целых рациональных функций
называется дробно иррациональной. Совокупность дробно иррациональных и целых рациональных называется рациональными функциями.
3) Функция, полученная с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми так и с дробными показателями и не являющиеся рациональными называются иррациональными.
y=√x, f(x)= 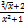
Рациональные и иррациональные функции образуют класс алгебраических функций.
4) Всякая функция, не являющаяся алгебраической, называется трансцендентной.
Элементарные функции
Алгебраические ф-ции Трансцендентные ф-ции
Рациональные ф-ции Иррациональные ф-ции
Целые ф-ции Дробные рац-ные ф-ции
Билет №3
Окрестность точки, предельная точка множества. Понятие стремления дискретной непрерывной величины к предельной точке. Определение предела функции непрерывного аргумента по Коши при х → х0 и х →∞ .
На числовой оси окрестность точки – любой интервал (открытый промежуток), содержащий данную точку. В частности открытый (не содержащий границ) промежуток (а – δ; а + δ) с центром в точке а называется δ-окрестностью точки а (положительное число δ – радиус δ-окрестности).
В n-мерном пространстве окрестность точки – любая область, содержащая данную точку.
Окрестность точки А в метрическом пространстве – любая область, содержащая точку А. В частности все точки М, расстояние от которых до точки А меньше некоторого положительного числа δ, образуют ее (т.е. точки А) сферическую окрестность радиуса δ с центром в точке А.
Точка Р называется предельной точкой множества М, если в любой окрестности точки Р имеется, по крайней мере, ещё одна точка множества М, кроме точки Р.
Оказывается, в любой окрестности предельной точки содержится бесконечное число точек множества М. Сама же предельная точка может как принадлежать, так и не принадлежать множеству М.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки aза исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Билет №4
Билет №5
Билет №6
Примеры.
1. Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция 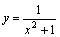 – бесконечно малая при x→+∞, т.е.
– бесконечно малая при x→+∞, т.е. 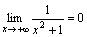 .
.
2. 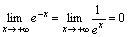 .
.
Билет №7
Доказательство.
Пусть 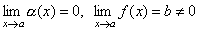 . Тогда 1/f(x) есть ограниченная функция. Поэтому дробь
. Тогда 1/f(x) есть ограниченная функция. Поэтому дробь 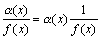 есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.
есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.
Билет №8
Билет №9
Теоремы о пределах (свойства пределов)
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
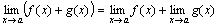 .
.
Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть 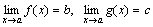 .Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,
.Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то
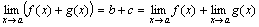 .
.
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
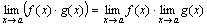 .
.
Доказательство. Пусть 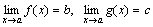 . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
. Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому 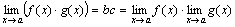 .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
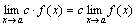 .
.
Следствие 2. Предел степени равен степени предела:
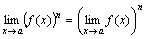 .
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
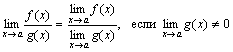 .
.
Доказательство. Пусть 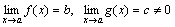 . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное
. Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное
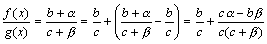 .
.
Дробь 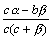 является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c2≠0.
является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c2≠0.
Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если
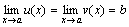
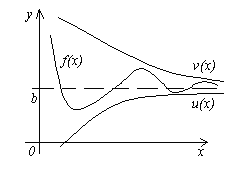 , то
, то 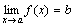 .
.
Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.
Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.
Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы 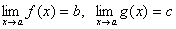 , то имеет место неравенство b≥c.
, то имеет место неравенство b≥c.
Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 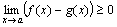 , или
, или 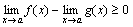 .
.
Билет №10
Первый замечательный предел
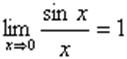
Из первого замечательного предела следует эквивалентность при х →0 следующих бесконечно малых величин: ах, sinax; tgax; arcsinax; arctgax. Это означает, что предел отношения двух любых из этих функций при х →0 равен 1.
С помощью этого соотношения можно вычислить массу других неопределенностей, которые без применения первого замечательного предела вычислялись бы сложнее.
Билет №11
Билет №12
Билет №13
Билет №14
Билет №15
Билет №17
Доказательство.
а) 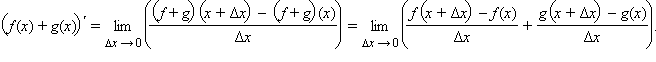 По свойству предела суммы получаем По свойству предела суммы получаем 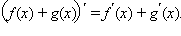 Постоянный множитель C можно выносить из-под знака производной: Постоянный множитель C можно выносить из-под знака производной:
В частности,
б) Функцию f · g можно записать в виде в) Для доказательства этой формулы заметим, что |
Если f дифференцируема, то 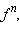 где
где 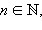 также дифференцируема, причем
также дифференцируема, причем
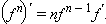 |
Если функция y = f (x) непрерывна и строго возрастает в окрестности точки 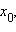 причем
причем 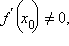 то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точкеy0 = f (x0), причем
то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точкеy0 = f (x0), причем
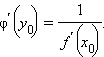 |
| ___________________________ |
Если функции y = f (x) и z = g (y) дифференцируемы в точках x0 и y0 = f (x0) соответственно, то сложная функция z = g (f (x)) дифференцируема в точке x0, причем
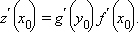 |
Следствием этой теоремы является тот факт, что дифференциал функции y = f (x) имеет один и тот же вид 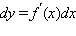 как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.
как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.
Если f (x) – четная функция, то 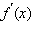 – нечетная; если f (x) – нечетная функция, то
– нечетная; если f (x) – нечетная функция, то 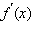 – четная.
– четная.
Пусть в окрестности точки t0 определены функции x (t) и y (t), причем x (t) непрерывна и строго монотонна. Пусть в этой окрестности существуют производные 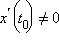 и
и 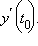 Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем
Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем
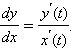 |
Билет №18
Билет №21
Билет №22
Билет №23
Билет №24
Билет №25
Билет №26
Теорема Тейлора
Пусть функцияr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 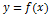 определена в некоторой точке x=a и в некоторой окрестности этой точки функция имеет производные до
определена в некоторой точке x=a и в некоторой окрестности этой точки функция имеет производные до 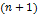 -го порядка, тогда существует точка x=Ɛ, такая, что выполняется формула Тейлора
-го порядка, тогда существует точка x=Ɛ, такая, что выполняется формула Тейлора
 , причем точка Ɛ лежит между x и a, т.е.
, причем точка Ɛ лежит между x и a, т.е. 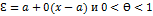 .
.
Последнее слагаемое в формуле Тейлора называется остаточным членом в форме Лагранжа.
При 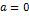 формула Тейлора называется формулой Маклорена:
формула Тейлора называется формулой Маклорена:
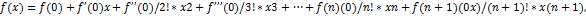
Билет №27
Формула Маклорена
Формулой Маклоренаназывается формула Тейлора при r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 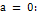
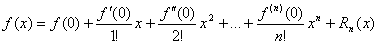
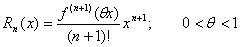
Мы получили так называемую формулу Маклорена с остаточным членом в форме Лагранжа.
| Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой- либо другой точке, естественно, при условии, что эти производные существуют. |
Однако, выбор числа а очень важен для практического использования. Дело в том, что при вычислении значения функции в точке, расположенной относительно близко к точке а, значение, полученное по формуле Тейлора, даже при ограничении тремя – четырьмя первыми слагаемыми, совпадает с точным значением функции практически абсолютно. При удалении же рассматриваемой точки от точки а для получения точного значения надо брать все большее количество слагаемых формулы Тейлора, что неудобно.
Т.е. чем больше по модулю значение разности 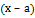 тем более точное значение функции отличается от найденного по формуле Тейлора.
тем более точное значение функции отличается от найденного по формуле Тейлора.
Кроме того, можно показать, что остаточный член Rn+1(x) является бесконечно малой функцией при ха, причем долее высокого порядка, чем (х – а)m, т.е. 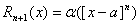
Таким образом, ряд Маклорена можно считать частным случаем ряда Тейлора.
Билет №28
Интервалы монотонности
Функция 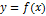 возрастает(убывает) на интервале
возрастает(убывает) на интервале 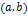 , если для
, если для 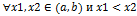 следует неравенство
следует неравенство 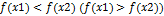 . Функция
. Функция 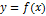 не возрастает (не убывает) на интервале
не возрастает (не убывает) на интервале 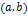 , если для
, если для 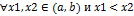 следует неравенство
следует неравенство 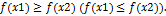
Теорема. Если 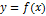 дифференцируема на
дифференцируема на 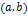 и
и 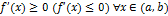 , то функция
, то функция 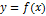 не убывает (не возрастает) на данном интервале.
не убывает (не возрастает) на данном интервале.
Билет №29
Билет №30
Билет №31
Билет №32
Билет №33
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при 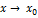 с какой-либо стороны функция
с какой-либо стороны функция 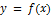 неограниченно возрастает по абсолютной величине, т.е.
неограниченно возрастает по абсолютной величине, т.е. 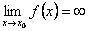 или
или 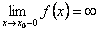 или
или 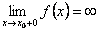 . Тогда из определения асимптоты следует, что прямая
. Тогда из определения асимптоты следует, что прямая 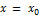 является асимптотой.
является асимптотой. 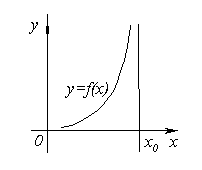 Очевидно и обратное, если прямая
Очевидно и обратное, если прямая 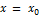 является асимптотой, т. о.
является асимптотой, т. о. 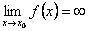 .
.
Таким образом, вертикальной асимптотой графика функции 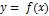 называется прямая, если
называется прямая, если 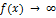 хотя бы при одном из условий
хотя бы при одном из условий 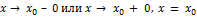
Следовательно, для отыскания вертикальных асимптот графика функции 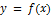 нужно найти те значения
нужно найти те значения 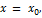 при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение
при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение 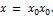
 НАКЛОННЫЕ АСИМПТОТЫ
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая 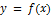 имеет наклонную асимптоту, то ее уравнение будет
имеет наклонную асимптоту, то ее уравнение будет 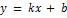 . Наша задача найти коэффициенты k и
. Наша задача найти коэффициенты k и 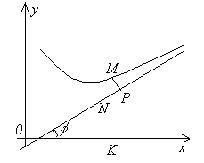 b.
b.
Теорема. Прямая 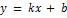 служит наклонной асимптотой при
служит наклонной асимптотой при 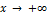 для графика функции
для графика функции 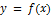 тогда и только тогда, когда
тогда и только тогда, когда 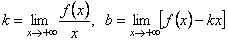 . Аналогичное утверждение верно и при
. Аналогичное утверждение верно и при 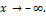
Билет №1
Множества, способы их задания. Операции над множествами (объединение, пересечение).
Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку.
Множества могут быть конечными, бесконечными и пустыми.
Множества могут быть заданы списком, порождающей процедурой, арифметическими операциями, описанием свойств элементов или графическим представлением.
1. Задание множеств списком предполагает перечисление элементов. Например, множество  состоит из букв
состоит из букв 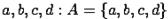 или множество
или множество 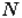 включает цифры
включает цифры 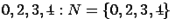 .
.
2. Задание множеств порождающей процедурой или арифметическими операциями означает описание характеристических свойств элементов множества: 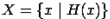 , т. е. множество
, т. е. множество 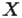 содержит такие элементы
содержит такие элементы 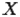 , которые обладают свойством
, которые обладают свойством 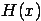 .
.
o 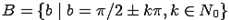 ,
, 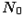 - множество всех натуральных чисел;
- множество всех натуральных чисел;
o 
3. Задание множества описанием свойств элементов: например, 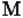 - это множество чисел, являющихся степенями двойки.
- это множество чисел, являющихся степенями двойки.
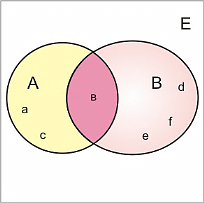
4. Графическое задание множеств происходит с помощью диаграмм Эйлера-Венна. Замкнутая линия-круг Эйлера - ограничивает множество, а рамка - универсальное пространство 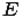 . Заданы два множества:
. Заданы два множества: 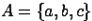 и
и 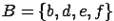 . Если элементов множеств немного, то они могут на диаграмме указываться явно.
. Если элементов множеств немного, то они могут на диаграмме указываться явно.
 Объединением множеств
Объединением множеств  и
и 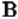 (
( 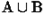 ) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств
) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств  или
или 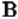 . Даны два множества:
. Даны два множества: 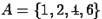 и
и 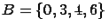 . Найдем множество
. Найдем множество 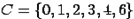 .
.
Пересечением множеств  и
и 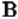 (
(  ) называется множество, состоящее из элементов, входящих как в множество
) называется множество, состоящее из элементов, входящих как в множество  , так и в множество
, так и в множество 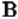 :
: 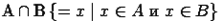 . Даны множества
. Даны множества 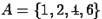 и
и 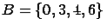 . Найдем их пересечение:
. Найдем их пересечение: 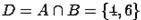 .
.
Билет №2
Функции, способы их задания, классификация.
Пусть даны 2 непустых множества A={x ∣x ∈ A}, B={y ∣y ∈ B} пусть f - некоторое отношение между А и В, если пара (х, у) является элементом отношения f, то говорят, что элементу у соответствует элемент х или элементу х сопоставляется элемент у.
Отношение fмежду А и В, при котором каждому элементу из А соответствует не более одного элемента из Вназывается функцией.
Различают 4 способа задания функции:
| х | х1 | х2 | х3 | х4 |
| у | у1 | у2 | у3 | у4 |
1. Табличный. Указывается значение аргумента x и соответствующе значение функции y=f(x).
2. Аналитический. Является наиболее важным для МА (мат. анализа), поскольку методы МА (дифференциального, интегрального счисления) предполагают этот способ задания. Одна и та же функция может быть задана различными формулами: y=∣sin(x)∣y=√1−cos2(x).
3. Графический. Область определения -- проекция данного графика на Ох, а множество значений -- проекция Д(f) на Оу.
4. Словестный. Например, y=[x] : x из R (Целой частью х из R называют любое целое число не превосходящее х).
Имеет место следующая классификация функций:
1) Функция вида Pn (x)=a0xn + a1xn-1 + a2xn-2 + … + an, где n ∊ N∪{0}, a0, a1, …, an ∊ R, называется целой рациональной функцией или многочленом степени n.
2) Функция, представляющая собой отношение двух целых рациональных функций
называется дробно иррациональной. Совокупность дробно иррациональных и целых рациональных называется рациональными функциями.
3) Функция, полученная с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми так и с дробными показателями и не являющиеся рациональными называются иррациональными.
y=√x, f(x)= 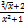
Рациональные и иррациональные функции образуют класс алгебраических функций.
4) Всякая функция, не являющаяся алгебраической, называется трансцендентной.
Элементарные функции
Алгебраические ф-ции Трансцендентные ф-ции
Рациональные ф-ции Иррациональные ф-ции
Целые ф-ции Дробные рац-ные ф-ции
Билет №3
Окрестность точки, предельная точка множества. Понятие стремления дискретной непрерывной величины к предельной точке. Определение предела функции непрерывного аргумента по Коши при х → х0 и х →∞ .
На числовой оси окрестность точки – любой интервал (открытый промежуток), содержащий данную точку. В частности открытый (не содержащий границ) промежуток (а – δ; а + δ) с центром в точке а называется δ-окрестностью точки а (положительное число δ – радиус δ-окрестности).
В n-мерном пространстве окрестность точки – любая область, содержащая данную точку.
Окрестность точки А в метрическом пространстве – любая область, содержащая точку А. В частности все точки М, расстояние от которых до точки А меньше некоторого положительного числа δ, образуют ее (т.е. точки А) сферическую окрестность радиуса δ с центром в точке А.
Точка Р называется предельной точкой множества М, если в любой окрестности точки Р имеется, по крайней мере, ещё одна точка множества М, кроме точки Р.
Оказывается, в любой окрестности предельной точки содержится бесконечное число точек множества М. Сама же предельная точка может как принадлежать, так и не принадлежать множеству М.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки aза исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Билет №4
Односторонние пределы. Необходимые и достаточные условия существования предела. Геометрический смысл предела.
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (или пределом справа).
Число A'называется пределом слева функции f(x) в точке a: 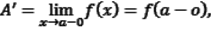 если
если
|A' - f(x)| < ε при 0 < a - x < δ (ε).
Аналогично, число A" называется пределом справа функции f(x) в точке a: 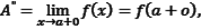 если
если
|A" - f(x) |< ε при 0 < x - a < δ (ε).
Для существования предела функции в точке необходимо и достаточно, чтобы f (a - 0) = f(a + 0).
Геометрический смысл предела функции:
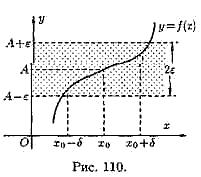
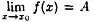 если для любой ε-окрестности точки Анайдется такая δ-окрестность точки хо, что для всех х1х0 из этой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε,ограниченной прямыми у=А+ ε, у=А-ε. Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
если для любой ε-окрестности точки Анайдется такая δ-окрестность точки хо, что для всех х1х0 из этой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε,ограниченной прямыми у=А+ ε, у=А-ε. Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
Билет №5

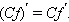
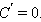
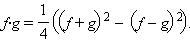 Но
Но 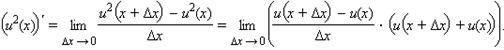 По свойству предела произведения получаем
По свойству предела произведения получаем 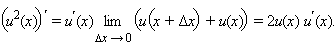 Используя доказанное равенство, получим, что
Используя доказанное равенство, получим, что 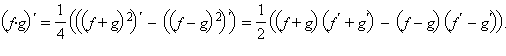 Раскрывая скобки и приводя подобные члены, получим формулу
Раскрывая скобки и приводя подобные члены, получим формулу 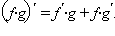
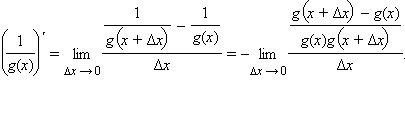 Воспользовавшись свойством предела частного, получим
Воспользовавшись свойством предела частного, получим 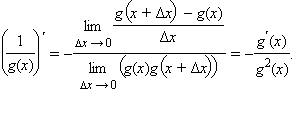 После этого представим
После этого представим 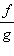 как произведение функций f и
как произведение функций f и 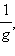 откуда и следует доказываемая формула.
откуда и следует доказываемая формула.