Направление выпуклости и точки перегиба

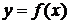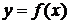График дифференцируемой функции называется выпуклым вниз на интервале , если дуга кривой на этом интервале расположена выше касательной, проведенной к графику функции в любой точке

Если же на интервале всякая касательная располагается выше дуги кривой, то график дифференцируемой функции 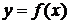на этом интервале называется выпуклым вверх.

Если функция дважды дифференцируема на и ( ), то ее график является выпуклым вниз (вверх) на .

Точки, в которых направление выпуклости меняется на противоположное, называются точками перегиба.

Достаточное условие точки перегиба. Пусть функция дважды дифференцируема в некоторой окрестности точки в которой или не существует. Если слева и справа от точки производная имеет противоположные знаки, то — точка перегиба.

Пример.

Найти интервалы выпуклости и точки перегиба графика функции

Находим вторую производную и приравниваем ее нулю. Получаем, что Следовательно, имеем два интервала выпуклости и Исследуя знак второй производной на каждом из этих интервалов, получаем, что график функции является выпуклым вверх на и выпуклым вниз на Следовательно, точка является точкой перегиба.

Асимптоты

Асимптотой графика функции 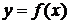называется такая прямая, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки от начала координат.

Если при этом координата точки стремится к конечному числу , то прямая является вертикальной асимптотой. Для существования вертикальной асимптоты в точке необходимо и достаточно, чтобы хотя бы один из пределов

Если же координата точки стремится к или , то имеем наклонную асимптоту для существования которой необходимо и достаточно существование двух пределов

и

При этом указанные пределы могут быть различными при (для левой наклонной асимптоты) и при (для правой наклонной асимптоты). Если то асимптоту обычно называют горизонтальной.

Пример.

Найти асимптоты графика функции

Функция определена на всей числовой прямой кроме точки Поскольку то прямая является вертикальной асимптотой.

Найдем и Следовательно, прямая является наклонной асимптотой графика функции при

Построение графиков функций

Исследование функций и построение их графиков можно проводить по следующей схеме.

1. Найти область определения функции.

2. Определить четность или нечетность данной функции, её периодичность. Если рассматриваемая функция четная или нечетная, то ее достаточно исследовать при положительных значениях аргумента из области ее определения и принять во внимание, что график четной функции симметричен относительно оси ординат, а график нечетной – относительно начала координат. Если рассматриваемая функция периодична, то её достаточно исследовать на одном периоде.

3. Непрерывность, классификация точек разрыва функции.

4. Нули функции. Интервалы знакопостоянства.

5. Определить интервалы монотонности функции, найти точки экстремума функции.

6. Исследовать функцию на выпуклость.

7. Найти асимптоты функции (наклонные, горизонтальные, вертикальные).

8. Построить таблицу. Для построения таблицы всю область определения разбиваем на промежутки нулями производной данной функции первого и второго порядка. Далее, на каждом из получившихся интервалов определяем их знак.

9. Построить график функции.

10. Найти область значения функции.

Пример.Исследовать функцию и построить график функции .

1. Областью определения данной функции является множество .

2. Данная функция ни четна, ни нечетна, не периодическая, т.е. общего вида.

3. Функция разрывная в точке , причем разрыв второго рода, т.к. .

4. Функция равна 0 при и при . Заметим, что при она отрицательна, а при – положительна.

5. . Нулями производной первого порядка являются точки и . Производная первого порядка положительна при и отрицательна при .

6. . Нетрудно установить, что производная второго порядка в нуль не обращается, положительна при и отрицательна при .

7. ,

Следовательно, прямая является наклонной асимптотой. Так как , то прямая является вертикальной асимптотой.

8.

	+		–		–		+
	–		–		+		+
		max				min

Найдем максимальное и минимальное значение функции

9.

10. Для нахождения области значения функции необходимо найти проекцию построенного графика на ось Oy. В данном случае областью значения является следующее множество .

Пример.Исследовать функцию и построить график функции .

1. Для нахождения области определения данной функции достаточно решить следующую систему неравенств . Следовательно, областью определения данной функции является множество .

2. Данная функция ни четна, ни нечетна, не периодическая, т.е. общего вида.

3. Функция является непрерывной на области определения.

4. Функция равна 0 при , положительна при и отрицательна при .

5. . Решением уравнения является .

6. . Решением уравнения является .

7. Так как и , то прямая является горизонтальной асимптотой. А так как , то прямая является вертикальной асимптотой.

8.

	+		–		–
	–		–		+
		max

9.

10. Областью значений данной функции является множество .

Пример.Исследовать функцию и построить её график.

1. Областью определения данной функции является множество .

2. Данная функция является нечетной, т.к. . Таким образом, достаточно её исследовать на множестве .

3. Функция является непрерывной на области определения.

4. Функция равна 0 при , положительна при и отрицательна при .

5. . Решениями уравнения являются точки .

6. . Решениями уравнения являются точки .

7. Так как , а , то наклонной и горизонтальной асимптоты нет. А так как , то прямые и являются вертикальными асимптотами.

8.

		–		–		+		+
		–		+		+		–
					min

9. По таблице, с учетом симметричности относительно начала координат строим график функции

10. Областью значения заданной функции является множество .