Тема №7 «Дискретные случайные величины»

Цель: познакомиться с понятием дискретной случайной величины, научиться составлять закон и функцию распределения дискретной случайной величины, находить её основные характеристики.

Краткие теоретические сведения:

Случайная величина–это переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений.

Случайная величина называется дискретной, если множество ее значений конечное, или бесконечное, но счетное.

Непрерывнаяслучайная величина – это величина, бесконечное, несчетное множество значений которой есть некоторый интервал числовой оси.

Случайные величины обозначаются большими латинскими буквами X, Y, Z, а их значения маленькими - x, y, z.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Для дискретной случайной величины закон распределения задаётся в виде таблицы.

			…
			…

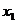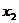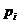- условие нормировки.

Используя таблицу можно закон распределения дискретной случайной величины изобразить графически в виде многоугольника (полигона) распределения.

Другая форма закона распределения – функция распределения 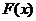, которая представляет собой вероятность того, что случайная величина Х примет значение, меньшее наперёд заданного х, то есть .

Функция распределения дискретной случайной величины есть разрывная ступенчатая линия, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений.

Свойства функции распределения:

1) 0≤F(x) ≤1,

2) функция распределения есть неубывающая функция,

3) F( )-F( ).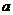

4) , .

Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности .

Свойства математического ожидания:

1) ,

2) ,

3) ,

4) (для независимых случайных величин)

5) ,

6) .

Вероятностный смысл:математическое ожиданиеприближенно равно среднему арифметическому наблюдаемых значений случайный величины.

Дисперсией случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания или .

СКО (средним квадратическим отклонением) случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии .

Свойства дисперсии:

1) ,

2) ,

3) ,

4) ,

5)

Вероятностный смысл: дисперсия – степень рассеяния значений случайной величины около её математического ожидания.

Модой 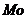случайной величины Х называется ее наиболее вероятное значение.

Медианой 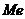случайной величины Х называется ее значение, находящееся в центре ряда распределения.

Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени этой величины: .

Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k -й степени отклонения этой величины от ее математического ожидания: .

- коэффициент асимметрии.

- эксцесс.

Пример. В семье трое детей. Случайная величина Х - число мальчиков в семье. Требуется:

а) найти закон распределения случайной величины Х,

б) построить многоугольник распределения случайной величины Х,

в) найти её функцию распределения ,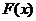

г) построить график ,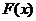

д) найти вероятность события Р(1<Х≤3)

е) найти М(Х), D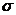(X), (X).

Решение: В семье может быть один, два, три или не быть мальчиков, то есть случайная величина Х принимает значения 0, 1, 2, 3.

Пусть А_i- событие, состоящее в том, что i-тый ребёнок мальчик, i=1,2,3.

Р(Х=0)=Р(Ā₁Ā₂Ā₃)= ,

Р(Х=1)=Р(А₁Ā₂Ā₃+Ā₁А₂Ā₃+Ā₁Ā₂А₃)= ,

Р(Х=2)=Р(Ā₁А₂А₃+А₁Ā₂А₃+А₁А₂Ā₃) = ,

Р(Х=3)=Р(А₁А₂А₃) = .

а) закон распределения случайной величины Х имеет вид:

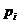б)

в)

г)

д) Р(1<Х≤3)=Р(Х=2)+Р(Х=3)= + = .

е) М(Х)= ,

М(Х²)= ,

D(X)=3-1,5²=0,75,

= .

Контрольные вопросы:

1. Дискретная случайная величина.

2. Закон распределения дискретной случайной величины. Многоугольник распределения вероятностей.

3. Математическое ожидание дискретной случайной величины. Её свойства и вероятностный смысл.

4. Дисперсия дискретной случайной величины. Её свойства и вероятностный смысл. Среднее квадратическое отклонение.

5. Функция распределения дискретной случайной величины. Свойства функции распределения.

6. Числовые характеристики среднего арифметического независимых и одинаково распределённых случайных величин.

7. Мода и медиана дискретных случайных величин.

Контрольные задания:

1. Имеется десять студенческих групп, насчитывающих соответственно 12, 10, 11, 8, 12, 9, 10, 8, 10 и 11 студентов.

а) составить закон распределения случайной величины Х, определяемой как число студентов в наугад выбранной группе,

б) построить многоугольник распределения случайной величины Х,

в) найти её функцию распределения F(х),

г) построить график F(х),

д) найти вероятность события Р(9<Х≤11)

е) найти М(Х), D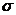(X), (X), , .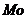

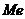2. Игральная кость брошена 4 раза.

а) составить закон распределения случайной величины Х, определяемой как число появления пятёрки.

б) построить многоугольник распределения случайной величины Х,

в) найти её функцию распределения F(х),

г) построить график F(х),

д) найти вероятность события Р(Х≤2),

е) найти М(Х), D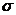(X), (X), , .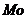

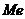Задания для домашней работы:

Произведены три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно: 0,4, 0,5 и 0,7.

а) составить закон распределения случайной величины Х, определяемой как число попаданий по мишени,

б) построить многоугольник распределения случайной величины Х,

в) найти её функцию распределения F(х),

г) построить график F(х),

д) найти вероятность события Р(1<Х≤3)

е) найти М(Х), D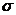(X), (X), 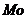, .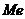