Дискретные случайные величины

Закон распределения вероятностей

Случайной величиной называется величина, которая в результате опыта может принять любые заранее неизвестные значения. Различают дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется такая, значения которой есть конечное или счетное множество фиксированных величин. Для описания поведения дискретной случайной величины X задают все значения х₁, х₂, ..., х_n, которые она может принять, и вероятности появления этих значений р₁, р₂, ..., р_n.

Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и соответствующих им вероятностей, причем

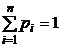: (1)

X	x1	x2	…	хn
р	p1	p2	…	pn

Ряд распределения можно задать графически, откладывая на горизонтальной оси значения X, а на вертикальной – соответствующие им значения вероятностей. Графическое представление ряда распределения называется многоугольником распределения.

Для дискретной случайной величины можно ввести понятие функции распределения F(x), которая равна вероятности случайного события, состоящего в том, что дискретная случайная величина X примет одно из возможных значений, меньших некоторого значения х, т.е. F(x) = Р(Х < х).

Если дискретные значения случайной величины расположены в порядке возрастания х₁, х₂, ..., х_n, то F(x) можно задать в виде:

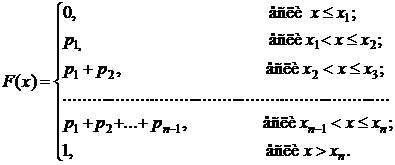
Функцию распределения можно представить графически в виде ступенчатой функции (рис. 2.1).

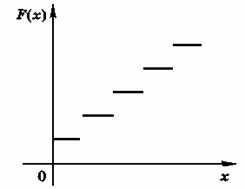
Рис. 2.1

2.1. Среди 10 лотерейных билетов имеется 4 билета с выигрышем. Наудачу покупают 2 билета. Написать закон распределения вероятностей числа выигрышных билетов среди купленных.

Решение. Пусть X – случайная величина числа выигрышных билетов среди купленных 2 билетов. Очевидно, что она может принимать значения: x₁ = 0, х₂= 1, x₃ = 2. Для определения вероятности появления каждого из этих значений воспользуемся следующей формулой:

Р(Х = т) = ,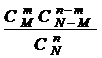

где т = 0, 1, 2 – число выигрышных билетов среди наудачу купленных n = 2 билетов;

N = 10 – всего имеющихся билетов;

М = 4 – число выигрышных среди всех 10 билетов.

Вычисляем соответствующие вероятности:

p₁ = P(X = 0) =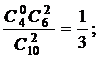

p₂ = P(X = 1) =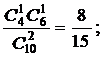

p₂ = P(X = 2) =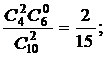

Для проверки вычислений сложим р₁ + р₂ + p₃ = ¹/₃ + ⁸/₁₅ + ²/_l5 = 1.

Следовательно, искомый закон распределения имеет вид

X
р	5/15	8/15	2/15

На рис. 2.2 представлен многоугольник распределения, полученного в задаче 2.1.

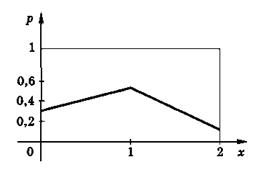
Рис. 2.2

2.2. Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске равна 0,7. Построить ряд распределения числа попаданий мяча в корзину.

Решение. Пусть X – случайная величина числа попаданий мяча в корзину. Баскетболист может не попасть ни разу, один раз, два раза и все три раза, т.е. х₁ = 0, х₂ = 1. х₃ = 2, х₄ = 3. Вероятности вычисляем по формуле Бернулли, при этом n = 3, р = 0,7, q = 0,3:

p₁ = P₃(0) = ;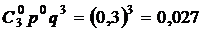

p₂ = P₃(1) =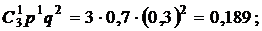

p₃ = P₃(2) =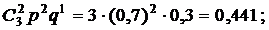

p₄ = P₃(3) =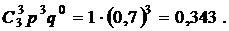

Проверяем выполнение соотношения (2.1):

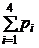= 0,027 + 0,189 + 0,441 + 0,343 = 1.

Тогда ряд распределения случайной величины числа попаданий мяча в корзину при трех бросках примет вид:

X
р	0,027	0,189	0,441	0,343

2.3. У продавца имеются изделия, полученные в равных количествах с трех фабрик. Вероятность того, что эти изделия отличного качества, для каждой фабрики соответственно со­ставляет 0,8; 0,7 и 0,9. Отобрано 2 изделия. Составить закон распределения количества изделий отличного качества среди отобранных.

Указание. Вначале вычисляется вероятность отбора изделия отличного качества: р = (0,8 + 0,7 + 0,9)/3.

2.4. Два покупателя независимо друг от друга делают по одной покупке. Вероятность того, что покупку сделает первый покупатель, равна 0,8, а вероятность того, что второй – 0,6. Случайная величина X – число покупок, сделанных покупателями. Описать закон распределения случайной величины X.

Решение. Очевидно, что сделать покупки могут либо оба покупателя, либо кто-то один, возможно также, что ни один покупатель ничего не купит. Следовательно, х₁ = 2, х₂ = 1, х₃ = 0.

Пусть событие А состоит в том, что первый покупатель сделал покупку, а событие В – в том, что второй покупатель сделал покупку. Тогда вероятность значения х₁ может быть подсчитана как вероятность события АВ. Так как А и В – независимые события, то:

р₁ = Р(Х = 2) = Р(АВ) = Р(А)Р(В) = 0,8 · 0,6 = 0,48.

Вероятность значения х₂ может быть подсчитана как вероятность события А 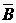или 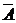В, т.е. р₂ = Р(Х = 1) = P(A 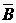+ 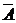В). Учитывая, что А 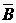и 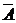В – события несовместные, р₂ = Р(А 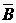) + Р( 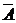В) = Р(А)Р( 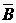) + Р( 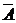)Р(В) = 0,8 · 0,4 + 0,2 · 0,6 = 0,44.

Вероятность значения х₃ есть вероятность события 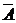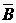: р₃ = Р(Х = 0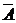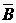) = Р( 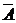) = Р( )Р( 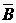) = 0,2 · 0,4 = 0,08. Соответственно, закон распределения примет вид:

X
р	0,48	0,44	0,08