Интегральное исчисление функций одной переменной
Борисова О.Н.
Интегральное исчисление функций одной переменной
Сборник контрольных задач и методических указаний
Королев, 2009
Борисова О.Н. Интегральное исчисление функций одной переменной. Сборник контрольных задач и методических указаний. - Королев: КИУЭС, 2009, 54 с.
Рецензенты: к.п.н., доцент Федосеева З.Р.
Сборник включает в себя задачи контрольных работ по курсу «Математика», раздел интегральное исчисление, и методических указаний по их решению. Предназначен для проведения практических занятий, контрольных работ, а также для самостоятельной работы студентов всех специальностей, изучающих данный курс.
| РЕКОМЕНДОВАНО Учебно-методическим советом КИУЭС Протокол № от 2009 г. | Учебное пособие рассмотрено и одобрено на заседании кафедры математики. Протокол № от 2009 г. |
| Зав. кафедрой математики и естественнонаучных дисциплин КИУЭС д.ф.-м.н., профессор Борисов В.Ф. |
Введение
Данное пособие содержит подборки задач, предназначенных как для самостоятельного решения, так и для проведения контрольных работ по курсу «Интегральное исчисление функций одного вещественного переменного». Все разделы содержат краткие формулировки основных понятий и теорем, необходимых для решения задач. В сборник включено 3 контрольные работы, каждая из которых приводится в 25 различных вариантах. Каждой контрольной работе предшествует разбор типового варианта.
Неопределённый интеграл
Первообразной от непрерывной функции f(x) называется любая функция F(x), для которой выполнено соотношение
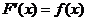 .
.
Для любой функции f(x) имеется много первообразных, однако все они отличаются друг от друга на константу: если F1(x) и F2(x) – первообразные от f(x), то 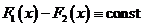 .
.
Совокупность всех первообразных называется неопределенным интегралом от f(x) и обозначается так:
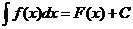 .
.
Здесь F(x) − любая фиксированная первообразная. Прямым дифференцированием можно проверить справедливость следующих соотношений.
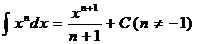 | 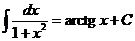 |
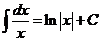 | 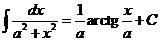 |
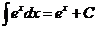 | 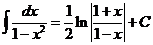 |
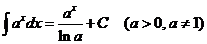 | 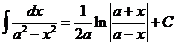 |
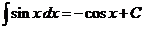 | 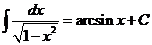 |
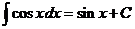 | 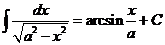 |
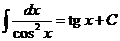 | 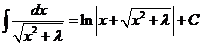 |
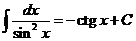 | 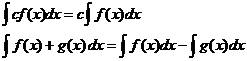 |
Частные случаи формулы 
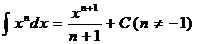 :
:
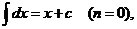
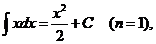
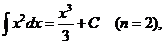
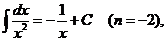
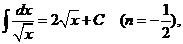
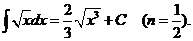
Имеется два основных приема вычисления неопределенных интегралов.
Замена переменной
Это наиболее часто используемый прием.
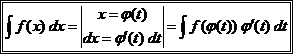 .
.
Интегрирование по частям
Интегрирование по частям позволяет «перебросить» производную с одного множителя, входящему в интегрируемую функцию, на другой

Во многих случаях угадать формулу замены переменной, упрощающей интегрируемую функцию, помогает занесение множителя под знак дифференциала
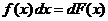 ,
,
где 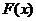 − произвольная первообразная функции
− произвольная первообразная функции 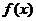 .
.
Так как производная постоянной функции равна нулю, а постоянный множитель можно выносить за знак дифференциала, для произвольных постоянных 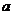 и
и 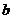 имеет место формула
имеет место формула
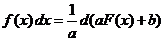 .
.
Рекомендуется запомнить следующие формулы
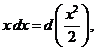 |  |
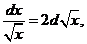 | 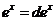 |
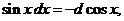 | 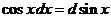 |
Разберем типичные ситуации , в которых используется интегрирование по частям.
1) Под знаком интеграла стоит 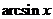 ,
, 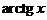 ,
, 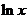 , умноженные на многочлен.
, умноженные на многочлен.
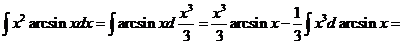
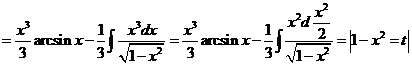
2) Интеграл вида  ,
,  ,
, 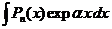 .
.
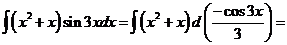
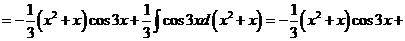
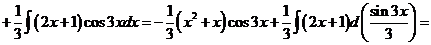
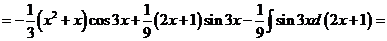
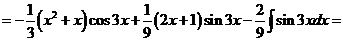
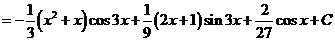
3) Интеграл вида 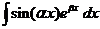 ,
, 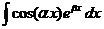 .
.
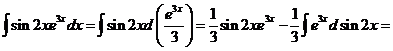
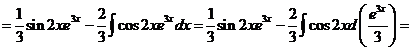
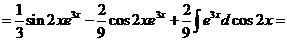
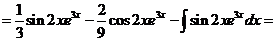
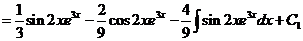
Обозначим F(x) произвольную первообразную функции 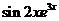 , получим
, получим
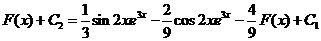
Выразим 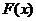
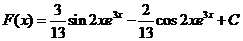 .
.
Замена переменной.
Пусть 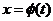 – произвольная непрерывно дифференцируемая функция, определённая на некотором отрезке
– произвольная непрерывно дифференцируемая функция, определённая на некотором отрезке 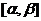 , причём
, причём 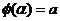 ,
, 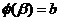 и
и 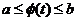 при
при 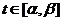 . Тогда
. Тогда
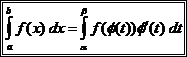 .
.
Интегрирование по частям.
 .
.
Приложение определённого интеграла.
Контрольная работа №1
Вариант 0
1) 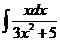 | 2) 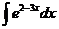 | 3) 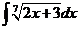 |
4) 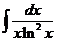 | 5) 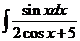 | 6). 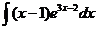 |
7) 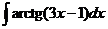 | 8) 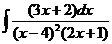 |
Решение варианта 0
1) 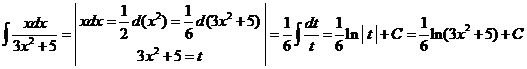 .
.
2) 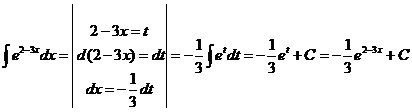 .
.
3) 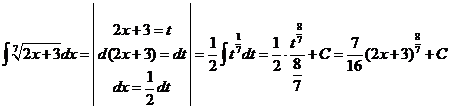 .
.
4) 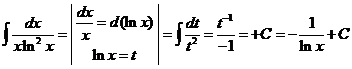 .
.
5) 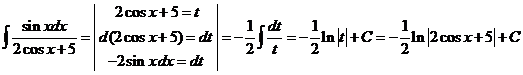 .
.
6) 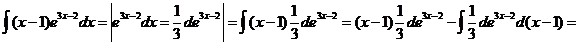
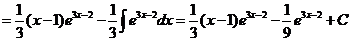 .
.
7) 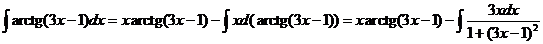
Найдем интеграл 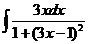 .
.
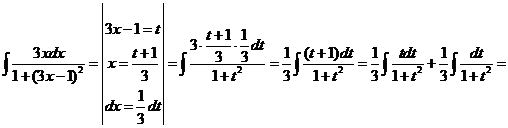
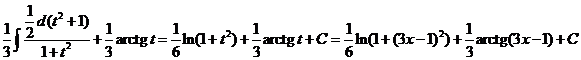 .
.
Ответ: 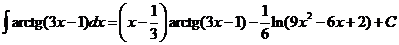 .
.
8) 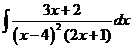 .
.
Разложим интегрируемую функцию на простые дроби
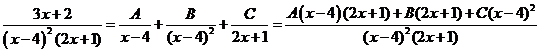 .
.
Приравняв числители, получим
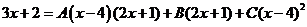 .
.
Для нахождения коэффициентов A, B, C подставим в данное тождество три различных значения переменной x:
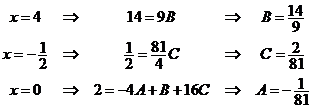
Таким образом
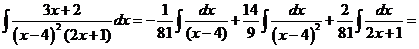
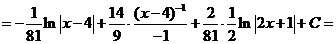
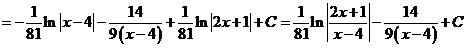
Вариант 1
1) 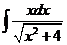 2)
2) 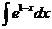 3)
3) 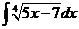
4) 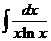 5)
5) 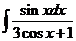 6).
6). 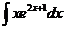
7) 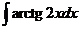 8)
8) 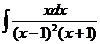
Вариант 2
1) 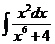
 2)
2) 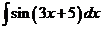 3)
3) 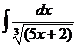
4) 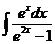 5)
5) 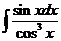 6)
6) 
7) 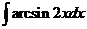 8)
8) 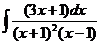
Вариант 3
1) 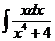 2)
2) 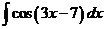 3)
3) 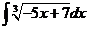
4) 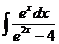 5)
5) 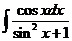 6)
6) 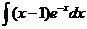
7) 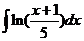 8)
8) 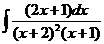
Вариант 4
1) 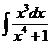 2)
2) 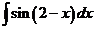 3)
3) 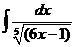
4) 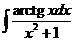 5)
5) 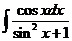 6)
6) 
7) 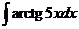 8)
8) 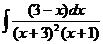
Вариант 5
1) 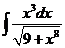
 2)
2) 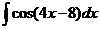 3.
3. 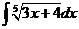
4) 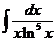 5)
5) 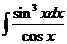 6.
6. 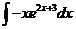
7)  8)
8) 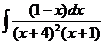
Вариант 6
1) 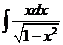 2)
2) 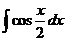 3)
3) 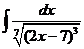
4) 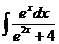 5)
5) 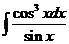 6)
6) 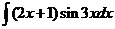
7) 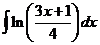 8)
8) 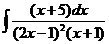
Вариант 7
1) 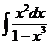 2)
2) 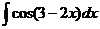 3)
3) 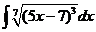
4) 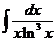 5)
5) 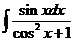 6)
6) 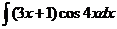
7) 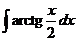 8)
8) 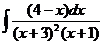
Вариант 8
1) 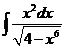 2)
2) 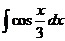 3)
3) 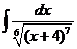
4) 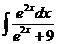 5)
5) 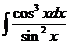 6)
6) 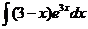
7) 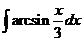 8)
8) 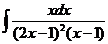
Вариант 9
1) 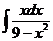 2)
2) 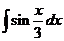 3)
3) 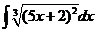
4) 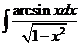 5)
5) 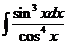 6)
6) 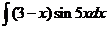
7) 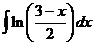 8)
8) 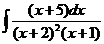
Вариант 10
1) 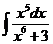 2)
2) 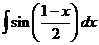 3)
3) 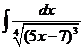
4) 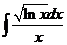 5)
5) 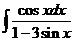 6)
6) 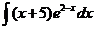
7) 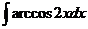 8)
8) 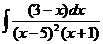
Вариант 11
1) 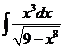 2)
2) 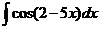 3)
3) 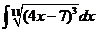
4) 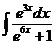 5)
5) 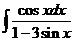 6)
6) 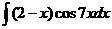
7) 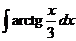 8)
8) 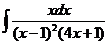
Вариант 12
1) 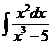
 2)
2) 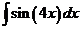 3.
3. 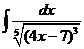
4) 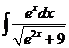 5)
5) 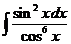 6.
6. 
7) 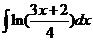 8)
8) 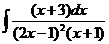
Вариант 13
1) 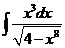 2)
2) 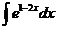 3)
3) 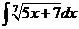
4) 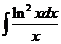 5)
5) 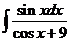 6).
6). 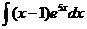
7) 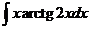 8)
8) 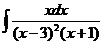
Вариант 14
1) 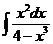 2)
2) 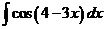 3)
3) 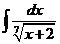
4) 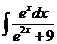 5)
5) 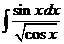 6)
6) 
7) 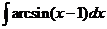 8).
8). 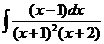
Вариант 15
1) 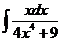 2)
2) 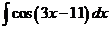 3)
3) 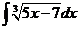
4) 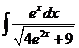 5)
5) 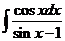 6)
6) 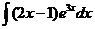
7) 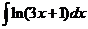 8)
8) 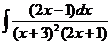
Вариант 16
1) 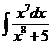 2)
2) 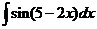 3)
3) 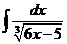
4) 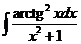 5)
5) 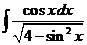 6)
6) 
7) 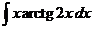 8)
8) 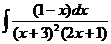
Вариант 17
1) 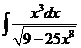
 2)
2) 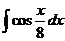 3.
3. 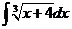
4) 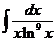 5)
5) 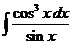 6.
6. 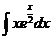
7)  8)
8) 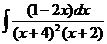
Вариант 18
1) 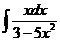 2)
2) 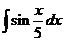 3)
3) 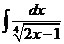
4) 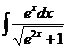 5)
5) 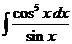 6)
6) 
7) 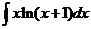 8)
8) 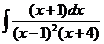
Вариант 19
1) 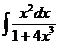 2)
2) 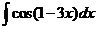 3)
3) 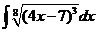
4) 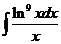 5)
5) 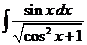 6)
6) 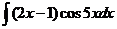
7) 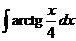 8)
8) 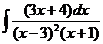
Вариант 20
1) 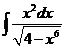 2)
2) 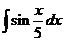 3)
3) 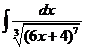
4) 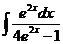 5)
5) 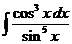 6)
6) 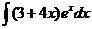
7) 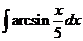 8)
8) 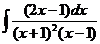
Вариант 21
1) 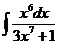 2)
2) 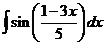 3)
3) 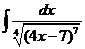
4) 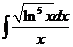 5)
5) 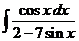 6)
6) 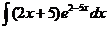
7) 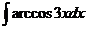 8)
8) 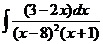
Вариант 22
1) 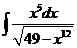 2)
2) 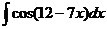 3)
3) 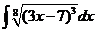
4) 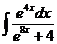 5)
5) 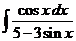 6)
6) 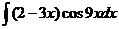
7) 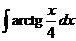 8)
8) 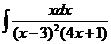
Вариант 23
1) 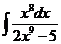
 2)
2) 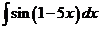 3)
3) 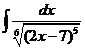
4) 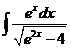 5)
5) 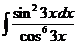 6.
6. 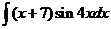
7) 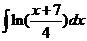 8)
8) 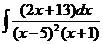
Вариант 24
1) 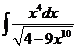 2)
2) 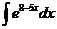 3)
3) 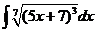
4) 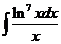 5)
5) 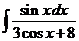 6).
6). 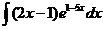
7) 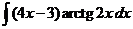 8)
8) 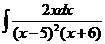
Вариант 25
1) 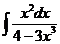 2)
2) 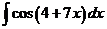 3)
3) 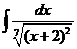
4) 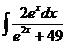 5)
5) 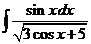 6)
6) 
7) 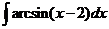 8).
8). 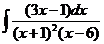
Контрольная работа №2
Вариант 0
1) 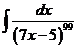 | 8) 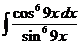 | 15) 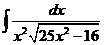 |
2) 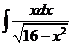 | 9) 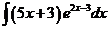 0 0 | 16) 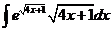 |
3) 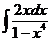 | 10) 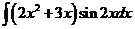 | 17) 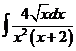 |
4) 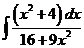 | 11) 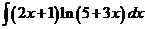 | 18) 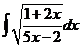 |
5) 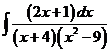 | 12) 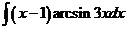 | 19) 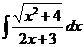 |
6) 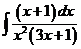 | 13) 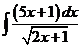 | 20) 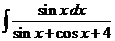 |
7) 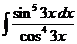 | 14) 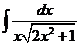 |
Решение варианта 0
1) 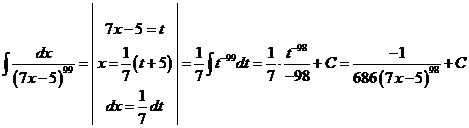 .
.
2) 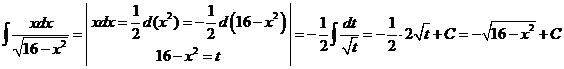 .
.
3) 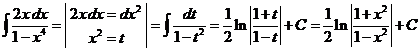 .
.
4) 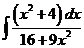
Поделим с остатком числитель подынтегральной функции на знаменатель.
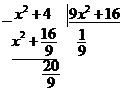
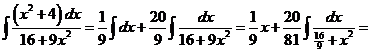
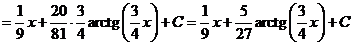 .
.
5) 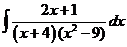
Разложим интегрируемую функцию на простые дроби
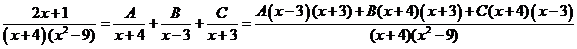 .
.
Приравняв числители, получим
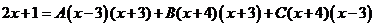 ,
,
откуда
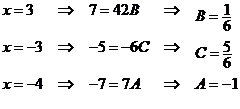
Таким образом
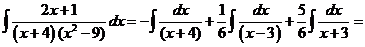
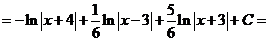
6) 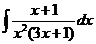
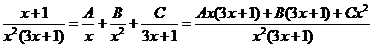
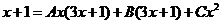
Откуда
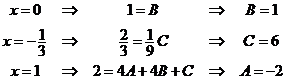
Таким образом
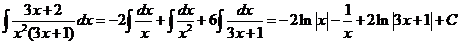
7) 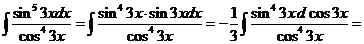
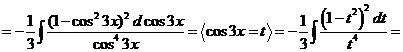
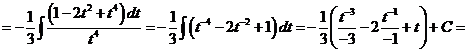
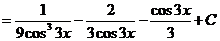 .
.
8)
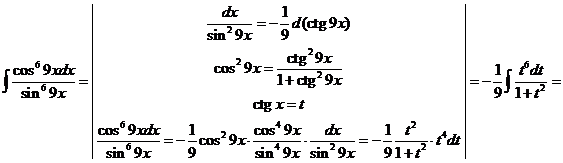
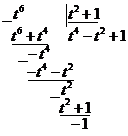
Таким образом
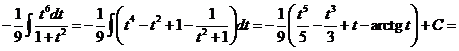
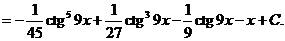
9) 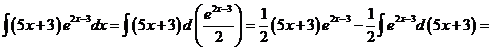
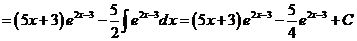 .
.
10) 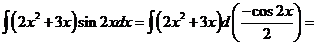
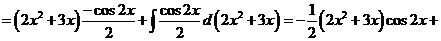
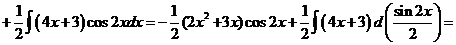
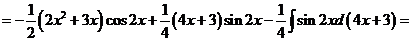
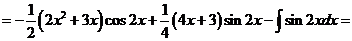
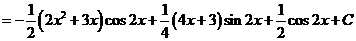 .
.
11) 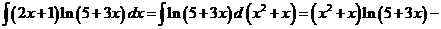
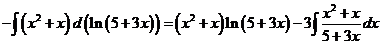
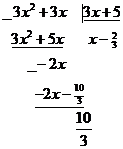
Таким образом,
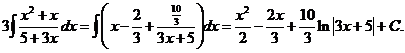
Ответ: 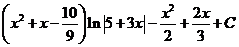 .
.
12) 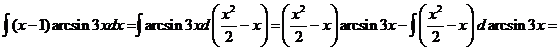
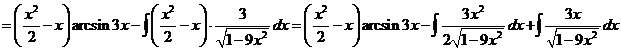
Вычисляем первый из двух оставшихся интегралов:
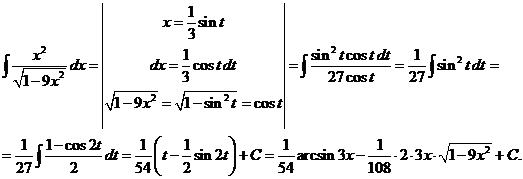
Второй интеграл равен
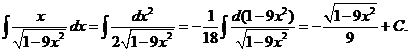
Ответ: 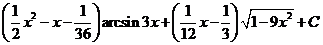 .
.
13) 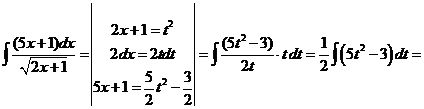
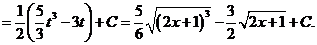
14) 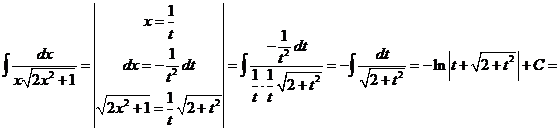
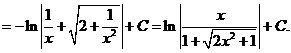
15) 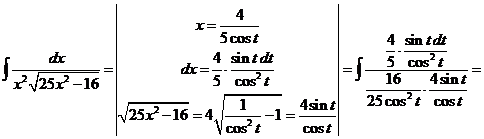
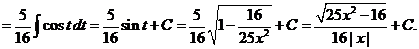
16) 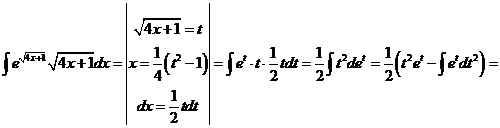
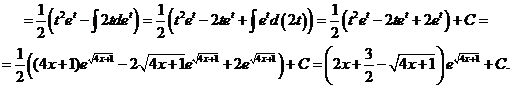
17)
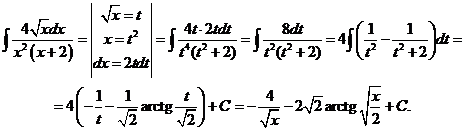
18) 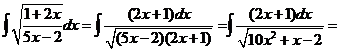
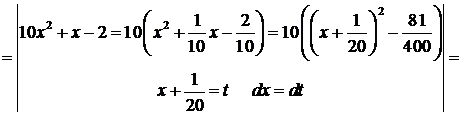
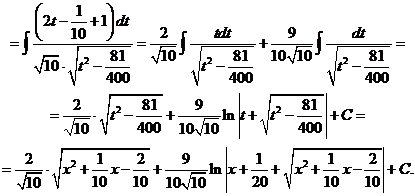
19)
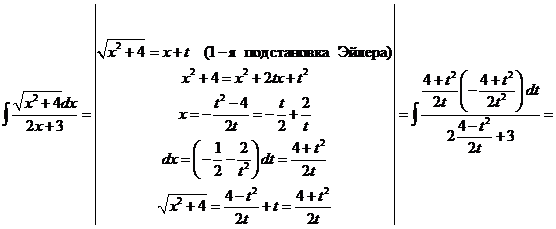
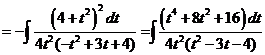 .
.
Разложим интегрируемую функцию на простые дроби. Поскольку дробь неправильная, сначала поделим с остатком ее числитель на знаменатель
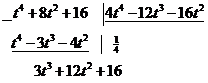
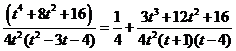
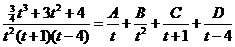
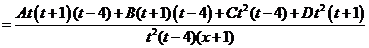
Приравняв числители, получим
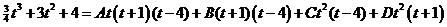
Откуда
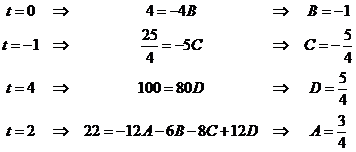
Таким образом
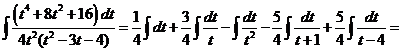
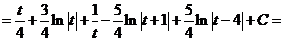
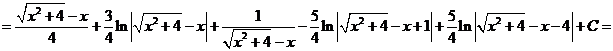
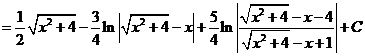
20)
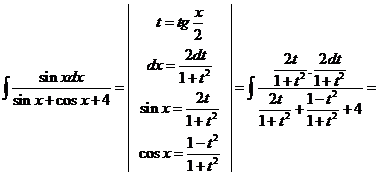
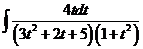
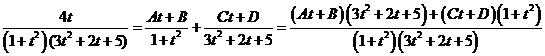
Приравняв числители, получим
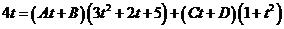
Откуда
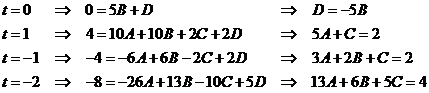
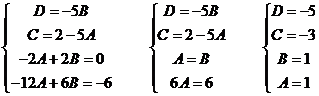
Таким образом
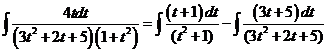
i) 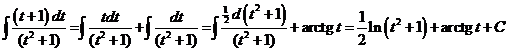
ii) 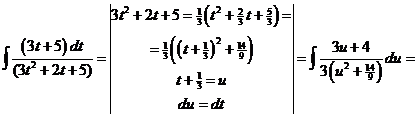
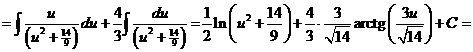
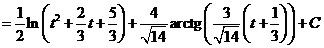
Ответ: 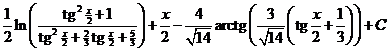
Вариант 1
1) 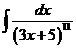 | 8) 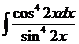 | 15) 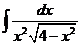 |
2) 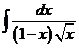 | 9) 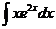 | 16) 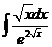 |
3) 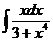 | 10) 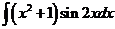 | 17) 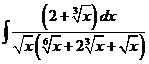 |
4) 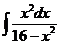 | 11) 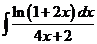 | 18) 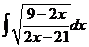 |
5) 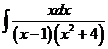 | 12)  | 19) 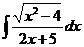 |
6) 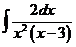 | 13) 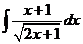 | 20) 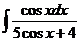 |
7) 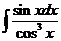 | 14) 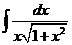 |
Вариант 2
1) 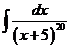 | 8) 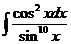 | 15) 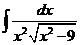 |
2) 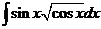 | 9) 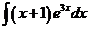 | 16) 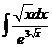 |
3) 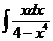 | 10) 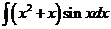 | 17) 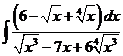 |
4) 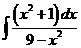 | 11) 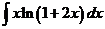 | 18) 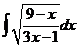 |
5) 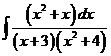 | 12) 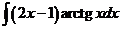 | 19) 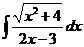 |
6) 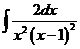 | 13) 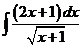 | 20) 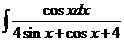 |
7) 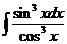 | 14) 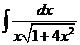 |
Вариант 3
1) 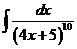 | 8) 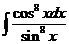 | 15) 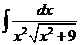 |
2) 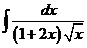 | 9) 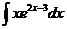 | 16) 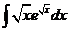 |
3) 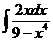 | 10) 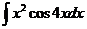 | 17) 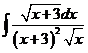 |
4) 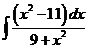 | 11) 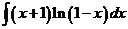 | 18) 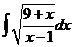 |
5) 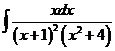 | 12) 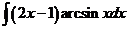 | 19) 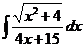 |
6) 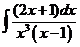 | 13) 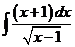 | 20) 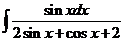 |
7) 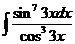 | 14) 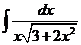 |
Вариант 4
1) 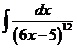 | 8) 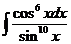 | 15) 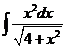 |
2) 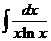 | 9) 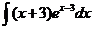 | 16) 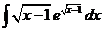 |
3) 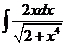 | 10) 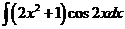 | 17) 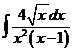 |
4) 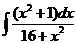 | 11) 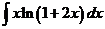 | 18) 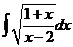 |
5) 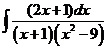 | 12)  | 19) 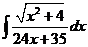 |
6) 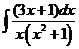 | 13) 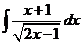 | 20) 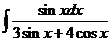 |
7) 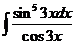 | 14) 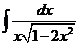 |
Вариант 5
1) 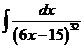 | 8) 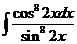 | 15) 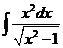 |
2) 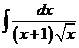 | 9) 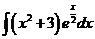 | 16) 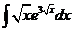 |
3) 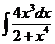 | 10) 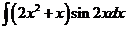 | 17) 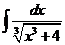 |
4) 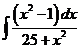 | 11) 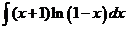 | 18) 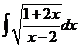 |
5) 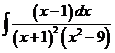 | 12)  | 19) 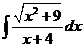 |
6) 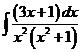 | 13) 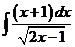 | 20) 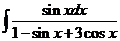 |
7) 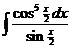 | 14) 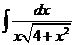 |
Вариант 6
1) 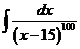 | 8) 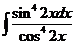 | 15) 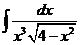 |
2) 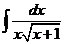 | 9) 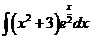 | 16) 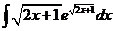 |
3) 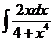 | 10)  | 17) 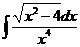 |
4) 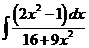 | 11 )  | 18) 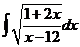 |
5) 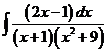 | 12)  | 19) 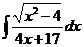 |
6) 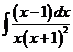 | 13) 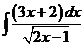 | 20) 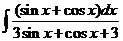 |
7) 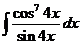 | 14) 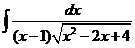 |
Вариант 7
1) 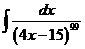 | 8) 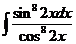 | 15) 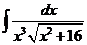 |
2) 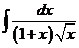 | 9) 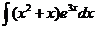 | 16) 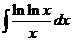 |
3) 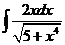 | 10) 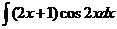 | 17) 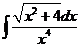 |
4) 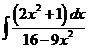 | 11)  | 18) 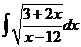 |
5) 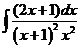 | 12) Наши рекомендации
|
