Выпуклость и вогнутость функции. Точки перегиба функции
Литература: [1], гл. 3, §3.3; [2], гл. V, §9.
Вопросы для самопроверки
1. Сформулируйте определения выпуклости и вогнутости функции, точек перегиба. Как находятся интервалы выпуклости и вогнутости и точки перегиба функции, заданной уравнением у = f(х)? Приведите примеры.
Асимптоты функции
1. Сформулируйте определение асимптоты функции.
Общая схема построения графиков функций
Литература: [1], гл. 3, §3.4, упр. 18, 20, 22, 24, 26, 27, 37; [2], гл. V, §11.
Вопросы для самопроверки
1. Изложите общую схему исследования функции и построения ее графика.
Неопределенный интеграл
Определение и свойства неопределенного интеграла
Литература: [1], гл. 5, §5.1-5.3, [2], гл. Х, §1-3.
Вопросы для самопроверки
1. Дайте определение первообразной функции.
2. Укажите геометрический смысл совокупности первообразных функций. Что называется неопределенным интегралом?
3. Напишите таблицу основных интегралов.
4. Докажите простейшие свойства неопределенного интеграла.
Основные методы интегрирования
Литература: [1], гл. 5, §5.4, упр. 1, 3, 5, 9, 18, 21, 22, 27, 29, 30, 31, 32, 35, 37, 39, 41, 43, 46, 49, 52, 54. [2], гл. Х, §4,6.
Можно использовать также [3], гл. IV, §1-3.
Вопросы для самопроверки
1. Найдите ò(2х – 1)3dх двумя способами: а) непосредственно как интеграл от степенной функции со сложным аргументом; б) раскрыв скобки и проинтегрировав полученную сумму. Покажите, что полученные результаты не противоречат друг другу.
2. Приведите формулу замены переменной в неопределенном интеграле.
3. Выведите формулу интегрирования по частям для неопределенного интеграла. Укажите типы интегралов, вычисление которых целесообразно производить с помощью метода интегрирования по частям.
Использование таблиц интегралов
Литература: [1], гл.5, §5.3, [2], гл. Х, §14.
Определенный интеграл
Литература: [1], гл.6, §6.1-6.6, упр.1, 4, 7, 10, 11, 12, 14, 16, 17, 21, 23, 24, 25, 27, 29, 36, 38, 40, 42, 44, 45, 46, 50; [2], гл. ХI, §1- 6, 8; §7.
Вопросы для самопроверки
1. Дайте определение определенного интеграла и укажите его геометрический смысл.
2. Пусть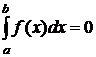 
, f(х) ¹ 0. Как это истолковать геометрически?
3. Покажите основные свойства определенного интеграла: а) постоянный множитель можно выносить за знак определенного интеграла; б) определенный интеграл от суммы нескольких функций равен сумме определенных интегралов от слагаемых; в)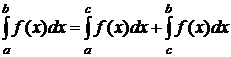 
, где а < с < b.
4. Докажите теорему о среднем для определенного интеграла и выясните ее геометрический смысл.
5. Докажите, что F(х) =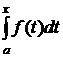 
является первообразной функцией для функции f(х). Выведите формулу Ньютона-Лейбница для вычисления определенного интеграла.
7. Напишите формулу замены переменной в определенном интеграле. Приведите пример.
8. Напишите формулу интегрирования по частям для определенного интеграла. Приведите пример.
9. Напишите формулу трапеций для приближенного вычисления определенного интеграла. Приведите пример.
Простейшие дифференциальные уравнения
Дифференциальные уравнения первого порядка
Литература: [1], гл.7, 7.1-7.3, упр.1-10,11-20, 21-30, 53, 54; [2], гл. XIII §1-11; [3], гл. X, §5.
Вопросы для самопроверки
1. Дайте определение дифференциального уравнения первого порядка и его общего и частного решения (интеграла). Сформулируйте задачу Коши для дифференциального уравнения первого порядка.
2. Дайте определение дифференциального уравнения с разделяющимися переменными. Изложите метод нахождения его общего решения. Приведите пример.
3. Дайте определение линейного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.
4. Дайте определение однородного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.