Декартова прямоугольная и полярная с-ма координат.
Декартова прямоугольная и полярная с-ма координат.
Прямоугольная с-ма координат на плоскости.
Две взаимноперпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу образуют прямоуг. с-му координат на плоскости. Ось Ох-ось абсцисс, ось Оу-ось ординат, точка О-начало координат. Плоскость, расположенную на осях Ох и Оуназыв. корд.плоскостью. Пусть М - произвольная точка, опустим перпендикуляр на ось Ох и Оу соотв. МА и МВ. Точке М на плоскости ставят в соотв-е 2 числа: абсциссу 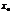 и ординату
и ординату  .
.  =расстоянию от О до А взятому со знаком «+» если А лежит правее О и «-» - если левее.
=расстоянию от О до А взятому со знаком «+» если А лежит правее О и «-» - если левее.  =расстоянию от О до В, взятому со знаком «+» если В выше О и «-» - если ниже.
=расстоянию от О до В, взятому со знаком «+» если В выше О и «-» - если ниже.
Абсцисса и ордината в точке М, наз-тсяпрямоуг. (декартовыми) координатами точки М. Введение прямоуг. с-мы координат позволяет установить взаимнооднозначноесоотв-е между всеми точками плоскости и множ-вом пар чисел, что дает при решении геом. задач применять алгебраические методы.
Полярная с-ма координат(П.С.К.).
П.С.К. состоит из нек-рой точки О, называемой полюсом и луча ОЕ, исходящего из точки О, называемого полярной осью. Кроме этого задается единица масштаба. Пусть задана полярная с-ма координат и пусть М-произв. точка плоскости. Положим r–это расстояние ОМ, j-угол, на к-рый нужно повернуть полярную ось для совмещения с лучом ОМ. Полярными координатами точки М наз-ют числа r и j, при этом r-1-ая координата, j-2-ая, называемая полярным углом. Точка М обозначается  , при чем r[0,+¥), j[0;2p].-рав-во 1. Однако в ряде случаев приходится рассматривать углы больше 2p, а также отриц. углы, т.е. отсчитываемые от полярной оси по часовой стрелке. Полюсу Осоотв-ет полярный радиус r=0, а полярный угол не определен.
, при чем r[0,+¥), j[0;2p].-рав-во 1. Однако в ряде случаев приходится рассматривать углы больше 2p, а также отриц. углы, т.е. отсчитываемые от полярной оси по часовой стрелке. Полюсу Осоотв-ет полярный радиус r=0, а полярный угол не определен.
Связь между полярными и Декартовыми координатами.
Будем предполагать, что начало прямоуг. с-мы координат находится в полюсе О, а полож. полуось абсцисс совпадает с направлением полярной оси. Пусть М имеет прямоуг. корд.  и полярные
и полярные  . (рис.) Не сложно показать, что
. (рис.) Не сложно показать, что  (1). Ф-лы (1) выражают прямоуг. корд.через полярные. Выразим полярные коорд. через прямоугольные.
(1). Ф-лы (1) выражают прямоуг. корд.через полярные. Выразим полярные коорд. через прямоугольные. 
 (2). Разделим второе ур-ние на первое
(2). Разделим второе ур-ние на первое  (3). Заметим, что ф-ла (3) определяет 2 значения полярного угла j. Из этих двух значений выбираем то, при к-ром вып-тсярав-во 1.
(3). Заметим, что ф-ла (3) определяет 2 значения полярного угла j. Из этих двух значений выбираем то, при к-ром вып-тсярав-во 1.
Простейшие задачи аналитической геометрии.
Расстояние между двумя точками.
Теорема. Для любых двух точек  и
и  на плоскости расстояние
на плоскости расстояние 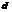 между ними выраж-тся ф-лой:
между ними выраж-тся ф-лой: 
Док-во:
1.Пусть х1 не = х2,и у1 не =у2
Тогда М1N=/ х2- х1/; М2N=/ у2- у1/;М1М2= 
2.Пусть х1=х2, и у1 не=у2,тогда
М1М2=/у2- у1/=  =
= 
Аналогич.если у2=у1
3.пусть х1=х2, у2=у1.тогда точки совпадают и расстояние равно 0; М1М2=0= 
Пр. Найти расстояние от (-1;2) до (3;-4)

Площадь треугольника.
Т. Для любых точек  не лежащих на одной прямой,
не лежащих на одной прямой,  выражается ф-лой
выражается ф-лой

3)Ур-ние прямой на плоскости
Пусть на плоскости задана прямоуг. с-ма координат и нек-рая линия  .
.
О. Ур-ние вида  связывающее переменные
связывающее переменные 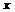 и
и 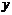 наз-тсяур-нием линии
наз-тсяур-нием линии  (в заданной с-ме координат); если этому ур-нию удовлетворяют координаты любой точки, лежащей на линии
(в заданной с-ме координат); если этому ур-нию удовлетворяют координаты любой точки, лежащей на линии  и не удовлетворяют координаты никакой другой точки, не лежащей на линии
и не удовлетворяют координаты никакой другой точки, не лежащей на линии  .
.
Примеры ур-ний линий на плоскости.
1. Рассм. прямую параллельную оси Оу. Обозначим буквой А точку пересечения А с Ох. Точка А(а,0).
Ур-ние х=а явл. ур-нием данной прямой, т.к. этому ур-нию удовлетворяют координаты любой точки М(а,у) и не удовлетворяют координатам ни одной точки не лежащей на этой прямой. Если а=0, то прямая совпадает с осью Оу.
2. Ур-ние 
 определяет множ-во точек плоскости, составляющих биссектрисы 1-го и 3-го координатных углов.
определяет множ-во точек плоскости, составляющих биссектрисы 1-го и 3-го координатных углов.
3.  . Данноеур-ние задает множ-во точек на плоскости, составляющих биссектрисы коорд. углов.
. Данноеур-ние задает множ-во точек на плоскости, составляющих биссектрисы коорд. углов.
4.  . Это ур-ние задает единственную точку на плоскости с коорд (0,0).
. Это ур-ние задает единственную точку на плоскости с коорд (0,0).  . Это ур-ние с центром в точке (0,0)
. Это ур-ние с центром в точке (0,0) 
Общее ур-ниепрямой.
Т. Каждая прямая на плоскости с прямоуг. с-мой корд.определяется ур-нием первой степени  , где α и b одновременно не равны 0. a2 + b2 ≠0 определяет нек-рую прямую на плоскости.
, где α и b одновременно не равны 0. a2 + b2 ≠0 определяет нек-рую прямую на плоскости.
Док-во:Пусть прямая имеет ур-ние  ,тогда кх-у+b,тоесть А=к,В=-1,С=b,следовательно Ур-ние прямой удовлетворяет общему виду Ур-ний;
,тогда кх-у+b,тоесть А=к,В=-1,С=b,следовательно Ур-ние прямой удовлетворяет общему виду Ур-ний;
Обратно если прямая задается этим урачнение,по условию хотябы один из коэффициентов отлтченотнуля делим на этот коэффициент,и получаем прямую которая соответствует Ур-нию с угловым коэффициентом.
Это ур-ние называют общим ур-нием прямой на плоскости.
Умножение матриц на число.
О. Произведение матрицы А на число aназ-тся матрицей aА, элементы к-рой равны произведению числа a на соотв. элемент матрицы А.
Умножение матриц.
О. Произведение матриц размерности m´n и матрицы В размерности 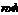 наз-тся матрица С размерности
наз-тся матрица С размерности 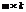 , элементы к-рой
, элементы к-рой 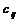 вычисляются как сумма произведений соотв-щих элементов
вычисляются как сумма произведений соотв-щих элементов 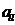
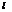 -строки матрицы А на
-строки матрицы А на 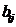
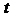 -столбца матрицы В.
-столбца матрицы В.
Пр. 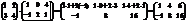
О.Квадратная матрица порядка nназ-тсяединичной. Обозначается 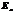 это матрица с единицами на главной диагонали.
это матрица с единицами на главной диагонали.
Св-ва умножения:
ü умножение не коммутативно, т.е. А*В¹В*А
ü умножение матриц ассоциативно, т.е. (А*В)*С=А*(В*С), если такие произведения существуют.
ü если А матрицы размерности m´n, В размерности 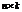 , то
, то 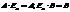
Транспонирование матрицы.
О. Если в матрице А размерности n´m все стороки заменить соотв-щими столбцами, то получим матрицу 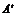 размерности m´n, к-руюназ-ют транспонированной матрицей А.
размерности m´n, к-руюназ-ют транспонированной матрицей А.
Св-ва транспонирования:
Y 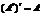
Y 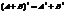
Y 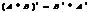
Элементарные преобразования строк матрицы:
* умножение строк матрицы на ненулевое действительное число;
* прибавление к одной строке матрицы другой, умноженной на нек-рое число.
Лемма: с помощью элементарных преобразований можно поменять местами две любые строки матрицы.
Ступенчатая матрица-матрица, обладающая след.св-вами:
1. если iтая строка нулевая то 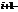 также нулевая.
также нулевая.
2. если первые ненулевые элементы 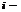 той строки и
той строки и 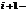 находятся соотв-но в столбцах с номерами k и p. Тогда k<p
находятся соотв-но в столбцах с номерами k и p. Тогда k<p
Теорема. Любую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований строк матрицы.
О.Ранг матрицы- число ненулевых строк в ступенчатом виде этой матрицы.
Пр. 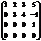
- ранг 3
Определители, их свойства.
О. Определителем 2-го порядка наз-тся число, вычисляемое по ф-ле 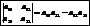
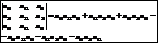
Определителем 3-го порядка соответствующих матрицы А называется число вычисляемое по формуле, которую удобно связывать со следующим правилом:
Т. Определитель 3-го порядка равен произведению элементов какой-либо строки(столбца) на соотв-щее алгебраическое дополнение.
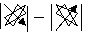
Определителем 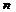 -го порядка, соотв-щим квадратной матрице
-го порядка, соотв-щим квадратной матрице 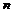 -го порядка, наз-тся число, равное сумме произведений элементов какой-либо строки(столбца) на их алгебраическое дополнение.
-го порядка, наз-тся число, равное сумме произведений элементов какой-либо строки(столбца) на их алгебраическое дополнение.
О. Минором 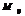 наз-ют определитель, полученный из данного путем вычеркивания
наз-ют определитель, полученный из данного путем вычеркивания 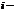 той строки и
той строки и 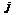 –того столбца. Алгебраическимдаполнением
–того столбца. Алгебраическимдаполнением 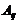 наз-ют число равное
наз-ют число равное 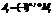
Св-ва определителя:
f Определитель треугольной матрицы равен произведению элементов главной диагонали
f Опред. матрицы с нулевой строкой или нулевым столбцом равен нулю
f При транспонировании матрицы, определитель не меняется.
f Если матрица А получается из матрицы В умножением каждого элемента нек-рой строки(столбца) на число 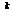 , то определитель равен
, то определитель равен 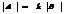
f Если матрица В получается из матрицы А перестановкой строк(столбцов), то определитель меняет знак.
f Определитель матрицы с пропорциональными строками(столбцами) равен 0.
f Определитель матрицы не меняется если к одной из строк прибавить другую, умноженную на нек-рое действительное число.
f Определитель произведения равен произведению определителей.
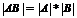 , где А и В- квадратные матрицы одног7о порядка.
, где А и В- квадратные матрицы одног7о порядка.
Обратная матрица.
Квадратная матрицаА порядка 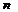 наз-тся обратимой, если сущ-ет такая матрица В, что
наз-тся обратимой, если сущ-ет такая матрица В, что 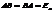 . В этом случае В-обратная для матрицы А и обозначают А-1.
. В этом случае В-обратная для матрицы А и обозначают А-1.
Т. Справедливы след.утверждения:
² если матрица обратима, то сущ-ет только одна ей обратная матрица.
² определитель обратимой матрицы отличен от 0.
² если А и В- обратимые матрицы порядка 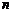 , то АВ- также обратима. Причем обратная для произведения равна В-1А-1. (АВ)-1= В-1А-1
, то АВ- также обратима. Причем обратная для произведения равна В-1А-1. (АВ)-1= В-1А-1
Док-во:
1)пусть В и С матрицы обратные матрице А тогда АВ=ВА=Е и АС=СА=Е,тогда В=В*Е=АС*В=ЕС=С,противоречиепоказывающее,что обратная матрица только одна.
2)т.к.А*А-1=Е,то /А*А-1/=/Е/=1, А-1 не=0;
3) (АВ)-1= В-1А-1докажем ,что В-1А-1 обратная для (АВ),
(АВ)* В-1А-1=А*Е*А-1=Е
(АВ)-1= В-1А-1=Е
Т. Квадратная матрица А обратима тогда и только тогда, когда ее определитель отличен от 0. Если 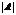 отличен от 0, то А-1=
отличен от 0, то А-1= 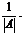
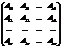
Пр. 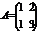
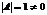 ,
, 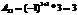 ;
; 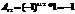 ;
; 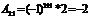 ;
; 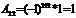
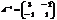
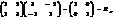
Понятие непрерывности ф-и.
Ф. 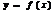 , определенная на
, определенная на 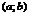 наз-тсянепрерывной в точке
наз-тсянепрерывной в точке 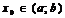 если
если 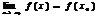
Т. Ф. 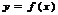 непрерывна в точке
непрерывна в точке 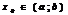 только тогда, когда
только тогда, когда 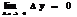
Док-во:
Предел при (х-х0) стремящемся к 0(f(x)-f(x0))=0;предел при х стремящемся к х0f(x)=f(x0)
Т. Если ф. 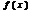 и
и 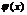 непрерывны в точке
непрерывны в точке 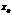 , то непрерывна в этой точке их сумма, разность, произведение, а также частное при усл.
, то непрерывна в этой точке их сумма, разность, произведение, а также частное при усл. 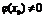
Док-во:
Док-во непосредственно следует из определения непрерывности и свойств
О. Ф. наз-тся непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
1-ая теорема Бальцама - Коши: Пусть ф. 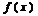 непрерывна на отрезке
непрерывна на отрезке 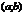 и на концах отрезка имеет значение разных знаков, тогда сущ-ет точка
и на концах отрезка имеет значение разных знаков, тогда сущ-ет точка 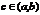 такая, что
такая, что 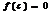
Т. Пусть ф. 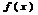 непрерывна на отрезке
непрерывна на отрезке 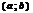 причем
причем  . Пусть
. Пусть 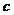 –число, заключенное между А и В, тогда сущ-ет точка
–число, заключенное между А и В, тогда сущ-ет точка 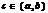 такая, что
такая, что 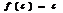
1-ая теорема Вейерштрасса: Если ф. 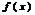 определена и непрерывна на
определена и непрерывна на 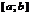 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
2-ая теорема Вейерштрасса: Если 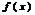 непрерывна на
непрерывна на 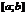 , то она достигает на этом отрезке своего наиб.инаим. значения.
, то она достигает на этом отрезке своего наиб.инаим. значения.
Системы линейных уравнений.
Совокупность ур-ний вида
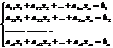 (1) - с-ма
(1) - с-ма 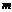 –линейных ур-ний с
–линейных ур-ний с 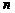 –неизвестным
–неизвестным 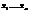
Числа 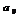 наз-тся коэффициентами с-мы. Числа
наз-тся коэффициентами с-мы. Числа 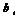 - свободными коэффициентами.
- свободными коэффициентами.
Решением с-мы (1) наз-тся совокупность чисел 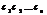 при подстановке к-рых в с-му (1) вместо
при подстановке к-рых в с-му (1) вместо 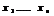 получаем верные числовые рав-ва.
получаем верные числовые рав-ва.
Решить с-му, значит найти все ее решения, либо доказать, что их нет.С-маназ-тся совместной, если она имеет хотя бы одно решение, несовместной- если решений нет. Матрица составлена из коэф-тов
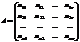 наз-тся матрицей с-мы (1).
наз-тся матрицей с-мы (1).
Если к данной матрице добавить столбец свободных коэф-тов, такую матрицу наз-ют расширенной матрицей с-мы
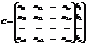
Критерий совместимости с-мы.
Т.Кронекера-Копелли: Для того, чтобы с-ма линейных ур-нийбыла совместно необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом матрицы с-мы.
Пр. 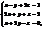
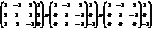
Метод Гаусса: применяется для произвольной с-мы линейных ур-ний.
О. С-му будем наз-тьступенчатой, если матрица имеет ступенчатый вид. При решении с-м линейныхур-ний нам понадобится след алгоритм:
1. Запишем расшир. матрицу и приведем ее к ступенчатому виду.
2. если ранги не равны, то с-манесовместна
3. если ранги равны и равны числу 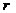 , то с-масовместна и остается записать ее решение
, то с-масовместна и остается записать ее решение
4. используя ступенчатый вид расширенной матрицы запишем соотв. ступенчатую с-му.
5. если 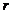 =
= 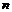 , т.е. ранг совпадает с числом неизвестных, то с-ма имеет единственное решение.
, т.е. ранг совпадает с числом неизвестных, то с-ма имеет единственное решение.
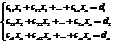 Двигаясь снизу вверх выражаем каждую из неизвестных.
Двигаясь снизу вверх выражаем каждую из неизвестных.
6. если 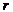 <
< 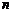 , то в с-ме
, то в с-ме 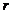 ур-ний и
ур-ний и 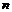 неизвестных. Неизвестные, к-рые первыми встречаются в ступенчатой с-ме (
неизвестных. Неизвестные, к-рые первыми встречаются в ступенчатой с-ме ( 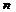 -неизвестных) назовем главными неизвестными, а остальные –свободными неизвестными. Снизу вверх выражаем каждую из главных неизвестных свободные неизвестные могут принимать любые значения, в этом случае с-ма имеет бесконечно много решений.
-неизвестных) назовем главными неизвестными, а остальные –свободными неизвестными. Снизу вверх выражаем каждую из главных неизвестных свободные неизвестные могут принимать любые значения, в этом случае с-ма имеет бесконечно много решений.
Правила Крамера:
С-ма линейных ур-нийназ-тсякрамеровской, если число ур-ний совпадает с числом неизвестных и определитель матрицы с-мы отличен от 0.
Т. Крамеровская с-ма имеет единственное решение, к-рое находится по ф-лам
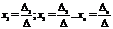 , где D-определитель матрицы с-мы, а
, где D-определитель матрицы с-мы, а 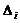 - определитель, полученный из D подстановкой вместо
- определитель, полученный из D подстановкой вместо 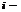 того столбца столбец свободных коэф-тов.
того столбца столбец свободных коэф-тов.
Док-во:
т.к матрица системы А не вырождена,то для нее существует обратная матрица А-1,вычисляемая по формуле:
А-1= 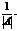
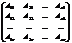
Запишем систему в виде матричного Ур-ния АХ=С,
А-1АХ= А-1С
ЕХ= А-1С;Х= А-1С
Предположим,что решение не единственное,тогда
АХ1=С и АХ2=С;АХ1=АХ2;Х1=Х2-данное протеворечиепоказывает,что решение единственное..найдемрешение Ур-ния Х= А-1С
Пр. 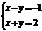
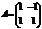 ;
; 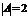 ;
; 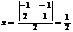 ;
; 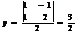 ;
; 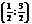
Предел ф-и.
О. Число А наз-тся пределом ф-и  , при
, при  (или в точке
(или в точке  ). Если для любого числа
). Если для любого числа  >0, сущ-ет такое число d>0, что при всех
>0, сущ-ет такое число d>0, что при всех  , удовлетворяющих условию 0<
, удовлетворяющих условию 0<  <dвып-тсянер-во
<dвып-тсянер-во  <e.
<e.
Для  0<
0<  <d (1) Þ
<d (1) Þ  <e.
<e.
Обозначается 
Геометрический смысл определения. Нер-во (1) означает, что  расположено от
расположено от  на расстоянии не более d, т.е.
на расстоянии не более d, т.е.  за исключением самой точки
за исключением самой точки  . Нер-во (2) означает, что значение ф-и
. Нер-во (2) означает, что значение ф-и 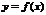 не выходит из интервала
не выходит из интервала  или
или  . След-но точки графика ф-и должны находится в полосе шириной 2e, если
. След-но точки графика ф-и должны находится в полосе шириной 2e, если 
Односторонние пределы.
О. Число А наз-тся правым(левым) пределом ф-и 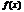 в точке
в точке  , если для "e>0сущ-етd>0, такое,что для всех
, если для "e>0сущ-етd>0, такое,что для всех 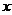 , удовлетворяющих рав-ву
, удовлетворяющих рав-ву  <
<  <
<  +d (
+d (  -d<
-d<  <
<  );
);  <e.
<e.
"e>0$d>0:" 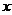
 <
<  <
<  +d (
+d (  -d<
-d<  <
<  )Þ
)Þ  <e.
<e.


Связь между односторонними пределами.
Ф-я  имеет в
имеет в  предел только тогда, когда в этой точке сущ-ет как левый так и правый предел и они равны. В этом случае предел ф-и равен одностороннему пределу.
предел только тогда, когда в этой точке сущ-ет как левый так и правый предел и они равны. В этом случае предел ф-и равен одностороннему пределу.
Пределы ф-и при стремлении аргумента к бесконечности.
О. Пределом ф-и  при
при  наз-тся число А такое, что для"e>0 $d>0:"
наз-тся число А такое, что для"e>0 $d>0:" 
 >dÞ
>dÞ  <e. Обозначают
<e. Обозначают  .
.
О. Число наз-тся пределом ф-и при  ®+¥ (
®+¥ (  ®-¥) если для "e>0 $d>0:"
®-¥) если для "e>0 $d>0:" 
 >d(
>d(  <-d)Þ
<-d)Þ  (
(  ).
).
Теорема Лагранжа.
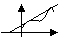 Пусть на
Пусть на 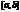 определена ф-я
определена ф-я 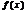 причем:
причем:
ü 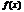 непрерывна на
непрерывна на 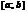
ü 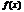 диффер. на
диффер. на 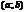
Тогда сущ-ет точка С, принадлежащ. 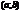 , такая, что
, такая, что 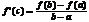
Док-во:
Введем в рассмотрение функцию F(x),для функции выполняется:1)F(x) не преывна на отрезке [a;b],как сумма не прерывных функции.2)F(x) ифференцируема на на интервале (a;b) как сумма дифференцируемых функции.3)F(a)=F(b)=0 следовательно существует такая т.С принадлежащая (a;b),что F’(C)=0,следовательно F’(C)= 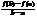
Теорема Коши.
Пусть 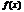 и
и 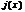 непрерывны на
непрерывны на 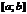 и дифференцируемы на
и дифференцируемы на 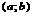 и пусть кроме того
и пусть кроме того 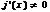 , тогда сущ-ет
, тогда сущ-ет 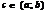 такая, что
такая, что 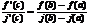 . Если в кач-ве
. Если в кач-ве 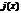 взять ф-ю.
взять ф-ю. 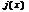 =
= 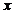 , то получим т. Лагранжа. Если т. Лагранжа положить
, то получим т. Лагранжа. Если т. Лагранжа положить 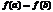 , то получим т. Коши.
, то получим т. Коши.
Теорема Лапиталля-Бернулли.
Пусть 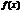 и
и 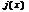 определены и дифф. на
определены и дифф. на 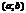 содержащим точку
содержащим точку 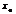 за исключением быть может самой точки
за исключением быть может самой точки 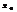 . Пусть предел при
. Пусть предел при 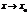 и
и 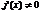 на
на 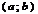 , тогда если сущ-ет конечный предел, при,
, тогда если сущ-ет конечный предел, при, 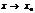
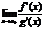 то сущ-ет и
то сущ-ет и 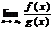 причем они равны
причем они равны
14)Исследование поведения ф-и и построение её графика.
Признак и ¯.
О. Ф-я 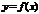 на
на 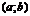 наз-тся : 1)постоянной, если
наз-тся : 1)постоянной, если 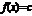 , где
, где 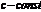 для
для 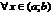 ;2)возрастающей, если для любых двух значений
;2)возрастающей, если для любых двух значений 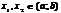 , таких что
, таких что 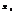 <
< 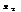 вып-тсянер-во
вып-тсянер-во 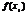 <
< 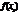 ; 3)убывающей, если из
; 3)убывающей, если из 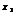 <
< 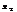 следует
следует 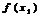 >
> 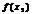
Достаточное условие и ¯ функции.
Если в данном промежутке 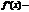 «+», то ф-я в этом промежутке, если
«+», то ф-я в этом промежутке, если 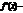 «-», то ф-я ¯. Если же на промежутке
«-», то ф-я ¯. Если же на промежутке 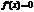 , то ф-я постоянна на этом промежутке.
, то ф-я постоянна на этом промежутке.
Док-во:
Рассмотрим функцию у= f(x) на интервале(а;b) рассмотрим произвольные х1 и х2,такие что х1  ч2,по теоремк Лагранжа сущт.С принадлежащая(х1;х2),такая ,что f(x2)- f(x1)=f’(c)(х2-х1);преположим,что производная на (а$b) положительна тогда f(x2)больше f(x1),соответственно если отриц.томеньше,если =0 то раны.В силу произвольности х1 и х2 функция fя вляетсяпостояннлй
ч2,по теоремк Лагранжа сущт.С принадлежащая(х1;х2),такая ,что f(x2)- f(x1)=f’(c)(х2-х1);преположим,что производная на (а$b) положительна тогда f(x2)больше f(x1),соответственно если отриц.томеньше,если =0 то раны.В силу произвольности х1 и х2 функция fя вляетсяпостояннлй
Экстремумы ф-и.
Рассм. нек-рую ф-ю 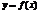 , определенную на
, определенную на 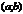 . Пусть
. Пусть 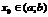 , d–нек-рое «+» число, d-окрестностью в точке
, d–нек-рое «+» число, d-окрестностью в точке 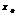 будем наз-ть интервал
будем наз-ть интервал 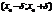 и обозначать
и обозначать 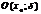 .
.
О. Если можно указать такую d–окрестность 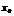 , принадлежащую
, принадлежащую 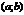 , что для всех
, что для всех 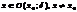 вып-тся
вып-тся 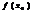 >
> 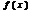 , то
, то 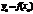 наз-ют максимумом ф-и
наз-ют максимумом ф-и 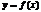 и обозначают
и обозначают 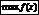 . Если же вып-тсянер-во , то минимумом –
. Если же вып-тсянер-во , то минимумом – 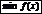
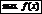 и
и 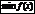 наз-ют экстремумом. Значение аргумента, при к-ром достигается экстремум, наз-ют точкой экстремума.
наз-ют экстремумом. Значение аргумента, при к-ром достигается экстремум, наз-ют точкой экстремума.
Т. (необходимое условие экстремума). В точке экстремума дифф. ф-и ее производная =0.
Если производная =0, то отсюда не следует, что 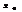 -точка экстремума.
-точка экстремума.
О. Точка, в к-рой производная =0 наз-тсястационарной. Точки, в к-рых произв. =0, а также точки, в к-рых производная не существует, либо =¥наз-ют критическими точками. Т.о. точки экстремума следует искать среди критических точек.
Т.(достаточное условие экстремума). Пусть ф-я 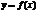 дифференцируема в нек-рой окрестности
дифференцируема в нек-рой окрестности 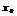 . Если в точке
. Если в точке 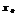 производная=0 и меняет знак при переходе через
производная=0 и меняет знак при переходе через 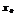 , то
, то 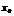 –точка экстремума, причем : 1)если произв. меняет знак с – на + это точка минимума; 2)с + на – точка максимума.
–точка экстремума, причем : 1)если произв. меняет знак с – на + это точка минимума; 2)с + на – точка максимума.
Т.Если в точке 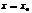 1-ая произв. дифф-мая. в нек-рой окрестности
1-ая произв. дифф-мая. в нек-рой окрестности 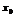 ф-и =0, а 2-ая произв. отлична от нуля, то
ф-и =0, а 2-ая произв. отлична от нуля, то 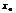 явл. точкой экстремума. Причем
явл. точкой экстремума. Причем 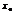 -
- 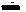 если
если 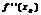 >0, и
>0, и 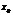 -
- 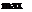 если
если 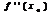 <0.
<0.
Направление выпуклости и точки перегиба.
О. График 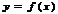 наз-тсявыпуклым вниз в данном промежутке, если он целеком расположен выше касательной в его производной точке и выпуклым вверх-если расположен ниже касательной.
наз-тсявыпуклым вниз в данном промежутке, если он целеком расположен выше касательной в его производной точке и выпуклым вверх-если расположен ниже касательной.
Т. Достаточный признак выпуклости графика ф-и.
Если 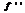 ф-и –«+» в данном промежутке, то график ф. явл. выпуклым вниз в данном промежутке. Если же
ф-и –«+» в данном промежутке, то график ф. явл. выпуклым вниз в данном промежутке. Если же 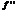 –«-«, то-выпуклым вверх.
–«-«, то-выпуклым вверх.
О. Точка, в к-рой меняется направление выпуклости наз-тсяточкой перегиба.
Т.(достаточный признак существования точки перегиба).
Если в точке 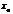
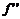
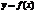 =0 и меняет знак при переходе через нее, то
=0 и меняет знак при переходе через нее, то 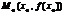 –точка перегиба.для х в 4 н выполняется.
–точка перегиба.для х в 4 н выполняется.
Асимптоты.
Если график ф-и сколь угодно близко приближается к прямой, то такую прямую наз-ют асимптотой.
О. Прямая 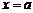 наз-тся вертикальной асимптотой графика ф-и
наз-тся вертикальной асимптотой графика ф-и 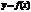 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 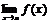 стремится к ¥.
стремится к ¥.
О.Предположим, что 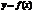 определена при сколь угодно больших по модулю значениях аргумента (будем рассм. «+» значения). Прямая
определена при сколь угодно больших по модулю значениях аргумента (будем рассм. «+» значения). Прямая 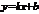 наз-тся наклонной асимптотой графика ф-и
наз-тся наклонной асимптотой графика ф-и 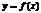 , если эта ф-я представлена в виде
, если эта ф-я представлена в виде 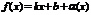 , где
, где 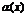 –бесконечно малая, то
–бесконечно малая, то 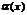 ®0, при
®0, при 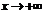 .
.
Т. (необходимое и достаточное условие существования наклонной асимптоты). График ф-и 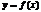 имеет при
имеет при 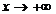 наклонную асимптоту
наклонную асимптоту 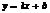 , если сущ-ют 2 конечных предела.
, если сущ-ют 2 конечных предела. 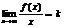 и
и 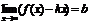
Исследование ф-и и построение графика:
I. Найти область определения (Д)
II. обл. значений
III. четность и периодичность
IV. точки пересечения с осями координат
V. изучить поведение ф-и при стремлении аргумента к концам обл. определения.
VI. точки экстремума и промежутки и ¯
VII. промежутки выпуклости ф-ий, точки перегиба
VIII. асимптоты графика
IX. построить график ф-и.
О. Ф-я 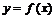 наз-тся четной, если: 1)
наз-тся четной, если: 1) 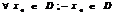 ; 2)
; 2) 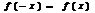
О. Ф-я 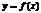 наз-тсяпериодической, если сущ-ет такое Т>0, что 1)
наз-тсяпериодической, если сущ-ет такое Т>0, что 1) 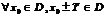
2) 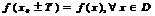
15)Скалярное, векторное и смешанное произведение векторов.
Предел.
Множ-во точек  , координаты к-рых удовлетворяют нер-ву
, координаты к-рых удовлетворяют нер-ву  <dназ-сяd -окрестностью точки
<dназ-сяd -окрестностью точки  .
.
О. Пусть нек-рая ф-я  определена в нек-рой окрестности точки
определена в нек-рой окрестности точки  кроме самой точки
кроме самой точки  . Число А наз-тся пределом ф-и
. Число А наз-тся пределом ф-и  при
при  ,
,  или
или  . Если для любого
. Если для любого  существует
существует  , такое что для всех
, такое что для всех  и
и  из
из  -окрестности точки
-окрестности точки  вып-тсянер-во
вып-тсянер-во  <e.
<e.




 ,
,  <e
<e
 Предел ф-и двух переменных обладает св-вами, аналогичнымисв-вам предела ф-и одной переменной. О.Ф-я
Предел ф-и двух переменных обладает св-вами, аналогичнымисв-вам предела ф-и одной переменной. О.Ф-я  наз-тсянепрерывной в точке если:
наз-тсянепрерывной в точке если:
1.она определена в 
2.имеет конечный предел при  ,
, 
3.этот предел = значению ф-и, т.е. 
 .
.
II. М-д замены переменной.
Теорема: если F(x)-первообр. f(x),  -дифференц. ф-я. Тогда
-дифференц. ф-я. Тогда  также имеет первообр. Причем
также имеет первообр. Причем

Док-во: По правилам диф. сложной ф-и  дает
дает  , т.е.
, т.е.  -одна из первообр. для
-одна из первообр. для  . След-но
. След-но
