Свойства криволинейного интеграла второго и его вычисление.

При определении криволинейного интеграла второго рода мы предполагали, что точки A0, A1, ..., An расположены на γ последовательно, так что соответствующие им точки t0, t1, ..., tn удовлетворяют условию a = t0 < t1 < ... < tn = b.

Это означает, что на кривой γ задано направление — от A к B. Если заменить направление на противоположное, то ∆xk,∆yk,∆zk и ∆tk поменяют знаки. Таким образом, получаем:

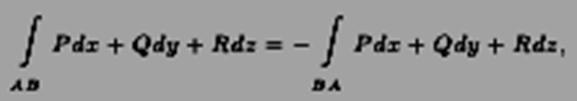
т.е. при изменении направления на кривой криволинейный интеграл второго рода меняет знак. Криволинейный интеграл второго рода обладает также свойствами линейности и аддитивности.

Вычисление.

Теорема 14.1. Пусть γ(t) = (x(t), y(t), z(t)) — гладкая дуга, P(x,y,z), Q(x,y,z), R(x,y,z) — непрерывные функции, определенные в точках дуги γ.

Тогда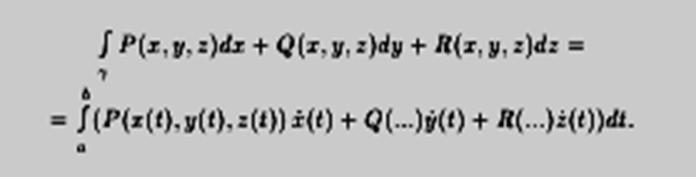

Формула Грина. Условие Эйлера.

Пусть в области D ⊂ R² определены функции P(x,y) и Q(x,y), пусть G ⊂ D — замкнутое связное множество, ограниченное кусочно гладкой кривой L. Зададим на L направление. Направление считают положительным, если при обходе L по такому направлению область G остаётся слева.

Теорема 15.1 (Формула Грина). Если P и Q имеют непрерывные частные производные первого порядка, то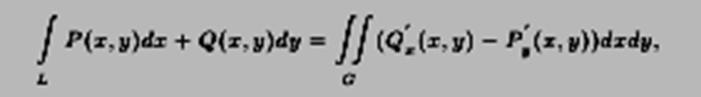

где L обходится в положительном направлении.

Условия Эйлера.

Выражение P(x,y)dx + Q(x,y)dy называют полным дифференциалом в области G, если существует функция, что dF = P(x,y)dx + Q(x,y)dy, ∀(x,y) ∈ G. При этом функцию F называют первообразной для полного дифференциала.

Теорема 15.2. Пусть в односвязной области G заданы функции P(x,y), Q(x,y), имеющие непрерывные производные первого порядка. Тогда следующие четыре условия равносильны:

1) Для любого замкнутого контура L ⊂ G выполняется условие

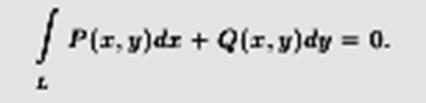
2) 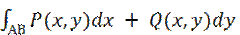не зависит от пути интегрирования для любых A, B ∈ G

3) Выражение P(x,y)dx + Q(x,y)dy является полным дифференциалом в области G.

4) Выполнены условия Эйлера: Py'(x, y)=Q'x(x, y), ∀(x,y)∈G.

Числовые ряды. Положительные ряды. Гармонический и геометрический ряды.

Числовой ряд.

Пусть задана числовая последовательность (an).

Последовательность сумм S1 = a1, S2 = a1 + a2, S3 = a1 + a2 + a3 и т.д. записывают в виде

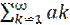и называют числовым рядом с элементами (или членами) ak.

Числовой ряд

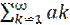называют сходящимся, если существует конечный предел S = lim_n→∞Sn последовательности частных сумм этого ряда. Если предел не существует или бесконечен, то говорят, что ряд расходится.

Суммой ряда называют предел последовательности его частных сумм.

Условия сходимости ряда.

Если ряд сходится, то lim_n→∞a_n = 0

Теорема 20.3. Если сходится ряд, то сходится и любой его остаток.

Положительные ряды

Числовой ряд 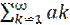называют положительным, если все его элементы ak > 0.

Теорема 20.4 (Критерий сходимости положительного ряда). Для сходимости положительного ряда необходимо и достаточно, чтобы последовательность (Sn) его частных сумм была ограничена (сверху).

Гармонический ряд.

Гармоническим рядом называют ряд 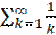. Теорема 20.5. Гармонический ряд расходится.

Геометрический ряд.

Если суммировать члены бесконечной геометрической прогрессии 1, q, q2, q3, ..., то получим числовой ряд, который, наряду с гармоническим рядом, служит ориентиром во множестве числовых рядов.

Ряд 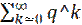q>=0 называют геометрическим рядом. если q >=1, то ряд расходиться. Если q < 1 - ряд сходится.