Оценка истинного значения измеряемой величины
Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины х1; х2; …; хn. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии σ (измерения равноточные) и распределены нормально (такое допущение подтверждается опытом). Истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.
Абсолютная погрешность среднего арифметического 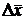 независимых измерений оценивается по формуле:
независимых измерений оценивается по формуле:
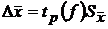 .
.
Интервальной оценкой величины хявляется доверительный интервал 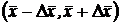 , в который попадает истинное значение с заданной доверительной вероятностью. Окончательный результат измерений запишется в виде:
, в который попадает истинное значение с заданной доверительной вероятностью. Окончательный результат измерений запишется в виде: 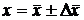 .
.
Относительная погрешность среднего арифметического: 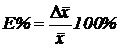
Вычисление абсолютной погрешности
косвенных измерений
Если искомая величина у связана с измеряемой х функциональной зависимостью: y=f(x1,x2,…xn), то такая величина называется косвенно измеряемой.
На практике достаточно часто требуется найти косвенно измеряемую величину и абсолютную и относительную погрешности косвенных измерений.
Пусть y=f(x) – функция зависит от одной переменной х. Были проведены измерения величины х»( 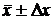 ), где
), где 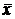 – среднее арифметическое прямых измерений величины х, а
– среднее арифметическое прямых измерений величины х, а 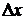 – погрешность прибора или абсолютная погрешность прямых измерений.
– погрешность прибора или абсолютная погрешность прямых измерений.
Значение косвенно измеряемой величины вычисляется по формуле 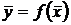 .
.
Абсолютная погрешность величины у вычисляется по формуле:
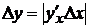 ,
,
где 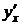 – производная у по переменной х.
– производная у по переменной х.
Относительная погрешность вычисляется по формуле: 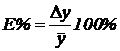 .
.
Пусть z=f(x,y) – функция, зависящая от двух переменных х и у. Проведены измерения величин х и у: х»( 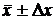 ) и
) и 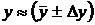 , где
, где 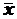 и
и 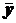 – средние арифметические прямых измерений величин х и у,
– средние арифметические прямых измерений величин х и у, 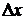 и
и 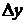 – погрешности приборов или абсолютные погрешности прямых измерений.
– погрешности приборов или абсолютные погрешности прямых измерений.
Значение косвенно измеряемой величины вычисляется по формуле 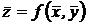 .
.
Абсолютная погрешность величины z=f(x,y) вычисляется по формуле:
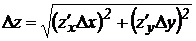 .
.
Относительная погрешность вычисляется по формуле 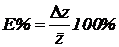
Решение задач
1. При исследовании плодов здоровых крыс были получены показатели масса тела плода: 2,58; 1,95; 2,04; 2,46; 2,56; 2,04; 2,46; 2,58; 2,56; 2,58; 3,04; 2,46. Найти приближенное значение величины с вероятностью 0,95.
Решение.
Найдем среднее арифметическое  ;
; 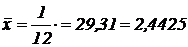
Найдем абсолютную погрешность: 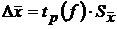 ; вычислим сначала
; вычислим сначала 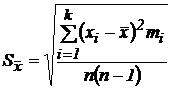 ;
; 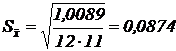 .
.
Составим расчетную таблицу:
| xi | mi | ximi | 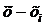 | 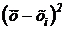 | 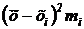 | |
| 1,95 | 1,95 | -0,49 | 0,2401 | 0,2401 | ||
| 2,04 | 4,08 | -0,4 | 0,16 | 0,32 | ||
| 2,46 | 7,38 | 0,02 | 0,0004 | 0,0012 | ||
| 2,56 | 5,12 | 0,12 | 0,0144 | 0,0288 | ||
| 2,58 | 7,74 | 0,14 | 0,0196 | 0,0588 | ||
| 3,04 | 3,04 | 0,6 | 0,36 | 0,36 | ||
| S | 29,31 | 1,0089 |
Найдем коэффициент Стьюдента 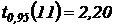 . Тогда
. Тогда 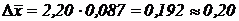 .
.
Примечание. При записи результата применяют следующее правило округления: абсолютную погрешность округляют до двух значащих цифр по избытку. В приближенном значении округляют так, чтобы сохранились все надежные цифры и одна сомнительная. Сомнительная цифра находится в том же разряде, что округленная в абсолютной погрешности.
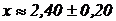
Относительная погрешность: 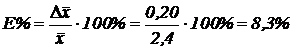 .
.
Ответ: приближенное значение случайной величины 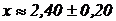 .
.
2. При исследовании содержания общего белка в сыворотке крови у 5 крыс были получены следующие статистические данные: 6,1; 6,2; 6,7; 6,6; 6,3 (г%). Найти приближенное значение величины, абсолютную и относительную погрешности. Оценить качество измерений с вероятностью 0,95.
Решение.
| xi | 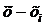 | 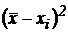 | |
| 6,1 | -0,28 | 0,0784 | |
| 6,2 | -0,18 | 0,0324 | |
| 6,3 | -0,08 | 0,0064 | |
| 6,6 | 0,22 | 0,0484 | |
| 6,7 | 0,32 | 0,1024 | |
| S | 0,268 |
Найдем среднее арифметическое: 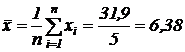 .
.
Найдем оценку средней квадратической погрешности среднего арифметического: 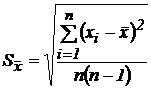 ;
; 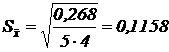 (г%).
(г%).
Абсолютная погрешность: 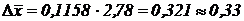 .
.
Приближенное значение: 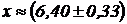 .
.
Относительная погрешность: 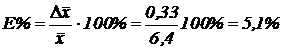 .
.
Ответ: приближенное значение случайной величины: 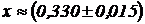 нм; качество измерений неудовлетворительное.
нм; качество измерений неудовлетворительное.
3. Вычислить объем куба с ребром 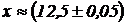 см. Оценить качество измерений.
см. Оценить качество измерений.
Решение. Объем куба 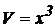 ;
; 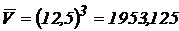 .
.
Найдем абсолютную погрешность: 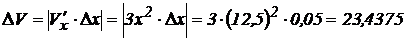 .
.
Тогда 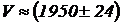 см3.
см3.
Найдем относительную погрешность: 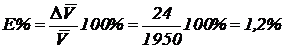 .
.
Ответ: 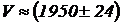 см3, качество измерений удовлетворительное.
см3, качество измерений удовлетворительное.
4. Вычислить объем прямоугольного параллелепипеда, если длины его ребер: 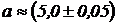 см;
см; 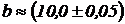 см;
см; 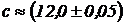 см. Оценить качество измерений.
см. Оценить качество измерений.
Решение. Объем прямоугольного параллелепипеда 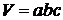 . Тогда
. Тогда 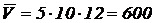 см3.
см3.
Найдем абсолютную погрешность: 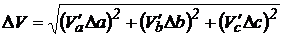 . Так как
. Так как 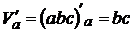 ;
; 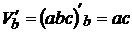 ;
; 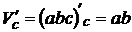 , то
, то 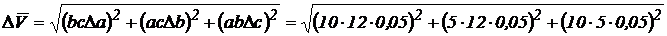
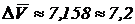 (см3).
(см3).
Найдем относительную погрешность: 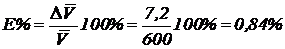
Ответ: Объем равен: 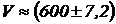 см3; качество измерений хорошее.
см3; качество измерений хорошее.
Самостоятельная работа студентов на занятии
1. Определить концентрацию сахарозы в растворе, абсолютную и относительную погрешности с вероятностью 0,99. Результаты наблюдений: 2,4; 2,7; 2,5; 2,6; 2,3. Оценить качество измерений.
2. Вычислить площадь круга с радиусом 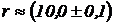 см, считая
см, считая 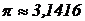 , т.е. как точное число, погрешность которого мала.
, т.е. как точное число, погрешность которого мала.
3. Вычислить площадь треугольника с основанием 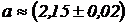 см и высотой
см и высотой 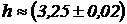 см.
см.
Задание на дом
Практика
1. Проведены равноточные измерения электрического сопротивления катушки. Полученные результаты представлены в таблице:
| хi | 6,27 | 6,271 | 6,272 | 6,273 | 6,274 |
| mi |
Найти приближенное значение сопротивления, абсолютную и относительную погрешности с доверительной вероятностью 0,99.
2. Вычислить площадь прямоугольника, если измерения длин сторон: 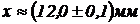 ;
; 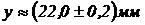 .
.
3. Вычислить объем цилиндра, если высота 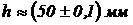 , радиус основания
, радиус основания  .
.
4. При фотоэлектроколориметрическом определении концентрации ацетилсалициловой кислоты на основании реакции с сульфатом меди и пиридином были получены следующие результаты: 99,2%; 99,0%; 98,9%; 99,3%; 98,8%; 99,1%. Вычислить среднее значение полученных результатов и абсолютную и относительную погрешности при доверительно при вероятности 0,95.
Теория
Подготовка к контрольной работе.
