Занятие 1. Понятие функции, предела и непрерывности функции. Производная функции

ПРАКТИКУМ ПО МАТЕМАТИКЕ

Методические указания по дисциплине

С2.Б.1 МАТЕМАТИКА

для студентов дневного отделения

Пятигорск 2011

УДК 519. 2’(075.8)

ББК 22.171я 73+32.81

В75

Рецензент: заведующий кафедрой информатики и математики ГОУ ВПО Пятигорского филиала Российского государственного торгово-экономического университета Коновцова М.М.

С.В. Воронина, Ю.А. Болгова, В.Т. Казуб

В 75 Практикум по математике (для студентов дневного отделения)/С.В. Воронина, Ю.А. Болгова, В.Т. Казуб.– Пятигорск: Пятигорская ГФА, 2011.–110 с.

Утверждено

На заседании ЭМС Пятигорской ГФА

Протокол №_337_ от

«09» сентября 2011 г.

Проф. В.В. Гацан

Практикум составлен в соответствии с программой по математике для студентов фармацевтических вузов и содержит краткие сведения из теоретического курса, задачи и примеры для тренинга, задания для самостоятельного решения, домашние задания. Практикум по математике включает список рекомендованной литературы.

УДК 519.2’(075.8)

ББК 22.171я 73+32.81

©Пятигорская государственная фармацевтическая академия, 2011

Содержание

Предисловие 7

Занятие 1.Понятие функции, предела и непрерывности функции. Производная функции 9

Занятие 2.Дифференциал функции. Производные и дифференциалы высших порядков. Применение производных к решению прикладных задач 18

Занятие 3.Производные и дифференциалы функции нескольких аргументов. Приложение полного дифференциала функции 27

Занятие 4.Неопределенный интеграл и его основные свойства. Основные методы интегрирования. 33

Занятие 5.Определенный интеграл и его основные свойства. Приложения определенного интеграла. 40

Занятие 6.Основные понятия теории вероятностей. Классическое и статистическое определение вероятности 50

Занятие 7.Теорема сложения вероятностей для несовместных событий. Случайные величины. Числовые характеристики дискретной случайной величины 56

Занятие 8.Понятие функции распределения и плотности распределения вероятностей непрерывной случайной величины. Числовые характеристики непрерывной случайной величины. Нормальный закон распределения 63

Занятие 9.Статистическое распределение выборки, дискретные и интервальные вариационные ряды. Точечные оценки параметров распределения. Доверительный интервал и доверительная вероятность. 74

Занятие 10.Погрешности измерений и их оценки. Погрешности прямых и косвенных измерений 87

Занятие 11.Контрольная работа 94

Занятие 12.Деловая игра «статистика знает все» 96

Творческая внеаудиторная работа студентов 97

Приложения 98

Библиографический список 109

Предисловие

Методическое пособие по курсу «Математика» разработано на кафедре физики и математики Пятигорской государственной фармацевтической академии для студентов первого курса специальности «Фармация» в соответствии с новым стандартом.

Курс математики рассчитан на 18 часов лекций и 36 часов практических занятий. Методическое пособие содержит разделы: основы дифференциального исчисления, основы интегрального исчисления, основы теории вероятностей, элементы математической статистики. Рассмотрены вопросы применения дифференциального и интегрального исчисления, математической статистики для решения прикладных естественнонаучных задач, некоторые вопросы основ моделирования процессов.

Данное пособие предназначено для самостоятельной подготовки студентов к занятию и включает в себя основной материал лекций, примеры и задачи с решениями, а также примеры для решения на занятии под руководством преподавателя и самостоятельной аудиторной и внеаудиторной работы. Для успешной подготовки к практическому занятию студенты должны выполнить домашнее задание по теме прошедшего практического занятия, руководствуясь методикой решения практических задач изученных на занятии. Затем внимательно прочитать материал следующего практического занятия в разделе «Краткие сведения из теоретического курса», материал лекции по теме занятия, учебника по математике, заучить основные определения и теоремы, разобрать решенные задачи и примеры, выписать в конспекте для самостоятельной работы все возникшие вопросы.

Практические занятия продолжительностью 3 академических часа поводятся один раз в неделю. Контроль проверки исходного уровня знаний осуществляется на основе тестовых заданий на каждом занятии, которые включают теоретический материал и практикум предыдущих занятий, теоретический материал текущего занятия. Контроль качества практических навыков проводится в виде самостоятельной аудиторной работы студентов на занятии, индивидуальных домашних самостоятельных заданий или расчетных заданий, включающих материал рассмотренного блока/раздела. Промежуточная и итоговая аттестация качества знаний осуществляется путем компьютерного тестирования и контрольной работы.

Для оценки знаний и умений студентов используется бально-рейтинговая накопительная система. За практическое занятие студент может получить 20 рейтинговых баллов из них:

· 0-2 домашнее задание;

· 0-10 баллов входной тест;

· 1 ведение конспекта занятия;

· 0-2 конспект текущей лекции;

· 0-5 самостоятельная работа на занятии по индивидуальным заданиям и/или индивидуальная домашняя работа.

Общая сумма баллов за текущую неделю составляет (при условии полного выполнения аудиторных занятий): 20 баллов за практическое занятие и 2 балла за посещение лекции. Кроме этого вводится система поощрительных баллов за активность на занятии 1-2 балла. Тестовый контроль (промежуточный, итоговый) оценивается в 10 баллов, контрольная работа в 20 баллов.

Изучение курса математики предполагает участие студента в одной из выбранных по желанию (назначенных преподавателем) творческих самостоятельных работ: реферат-презентация, доклад на занятии, подготовка викторины и прочие.

Зачтено по курсу математика студент может получить, если количество баллов составляет 60% и выше от общего количества рейтинговых баллов, отсутствуют пропущенные и неотработанные лекции, практические задания, выполнены тестовый промежуточный и итоговый контроль, выполнена контрольная работа и расчетные индивидуальные задания.

Желаем успехов в освоение новых знаний!

Основные теоремы о пределах

Теорема 1. Предел постоянной равен самой постоянной: .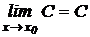

Теорема 2. Предел алгебраической суммы двух функций равен сумме их пределов при условии, что эти пределы существуют:

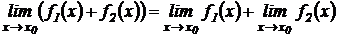
Теорема 3. Предел произведения двух функций равен произведению пределов, если последние существуют:

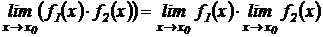
Следствие 1. Постоянный множитель может быть вынесен за знак предела: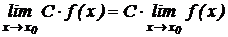

Следствие 2. Предел степени с натуральным показателем равен той же степени предела: .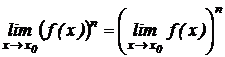

Теорема 4. Предел отношения двух функций равен отношению их пределов, если последние существуют, и предел делителя отличен от нуля:

.

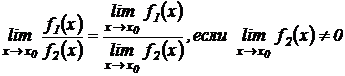Производная функции

Пусть функция y=f(x) определена на некотором интервале.

Определение. Приращением аргумента называется разность между двумя значениями аргумента Δх= х - х₀.

Разность между двумя значениями функции называется приращением функции: Δy= Δf = f(x₀-x)-f(x₀)

Определение. Если функция f (x) определенная на промежутке (a; b), то производной функции f(x) в точке 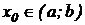называется предел отношения приращения функции 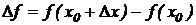к приращению независимого переменного 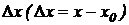при Dx, стремящемся к нулю .

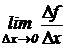Производная сложной функции

Теорема (о производной сложной функции): Если функция 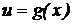имеет производную 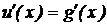в точке х, а функция 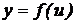– производную 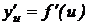в соответствующей точке и, то сложная функция 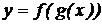в данной точке x имеет производную 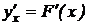, которая находится по формуле .

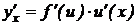Механический смысл производной: мгновенная скорость прямолинейного движения есть производная от пути S по времени t.

Физический смысл производной: если y=f(x) описывает какой-либо физический процесс, то производная 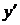есть скорость протекания этого процесса.

Геометрический смысл производной: производная 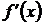в точке х равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна х.

Таблица основных формул дифференцирования

1. .

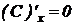2. .

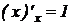3. .

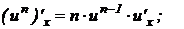
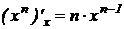4. .

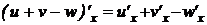5. .

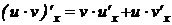6. .

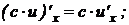
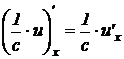7. .

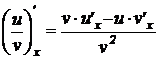8. ; .

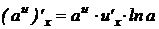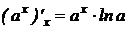9. .

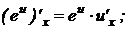
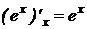10. .

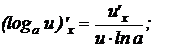
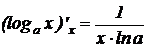11. .

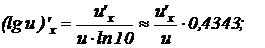
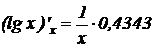12. .

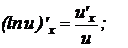
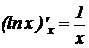13. .

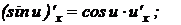
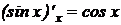14. .

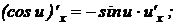
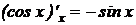15. .

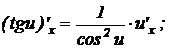
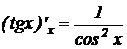16. .

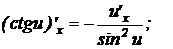
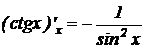Решение задач

Пример 1.1. Вычислить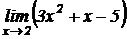

Решение. Используя теоремы о пределах, находим:

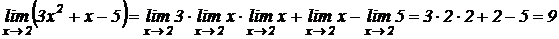
Часто бывает, что функция y=f(x) при x®x₀ не определена, но 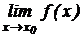существует. В этом случае для отыскания предела нужно предварительно выполнить преобразование функции.

Пример 1.2. Вычислить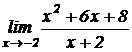

Решение. Применяя непосредственно теоремы о пределах, имеем:

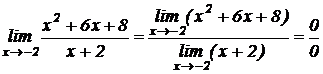
Выражение вида 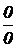в математике носит название неопределенности вида 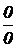. В этом случае для отыскания предела нужно предварительно преобразовать дробь, разложив числитель x² + 6x+8 на множители: x² + 6x+8 = (x + 2)×(x + 4). Квадратный трехчлен ax²+bx+c разлагается на множители ax²+bx+c=a(x – x₁)×(x – x₂), где x₁ и x₂ – корни уравнения ax²+bx+c которые определяются по формуле:

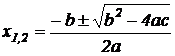
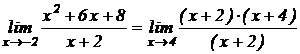
Сократив числитель и знаменатель на x + 2, получим:

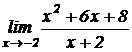
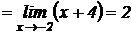
Пример 1.3. Вычислить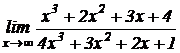

Решение. Применив теоремы о пределах, получим неопределенность вида 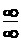. Для ее раскрытия числитель и знаменатель дроби разделим на старшую степень хв знаменателе, т. е. на хи получим:

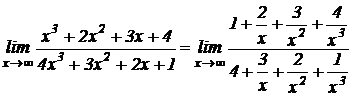
Так как неопределенность вида 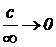, то .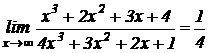

Пример 1.4. Найти производную функции .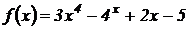

Решение.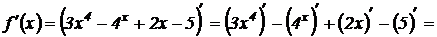

.

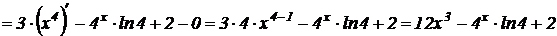Пример 1.5. Найти производную функции .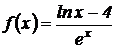

Решение.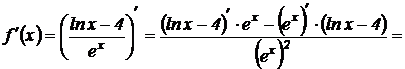

.

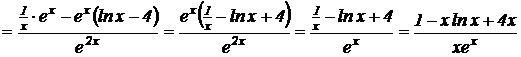Пример 1.6. Найти производную функции .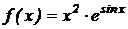

Решение.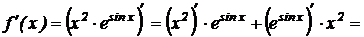

.

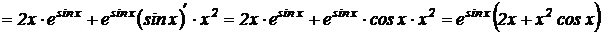Пример 1.7. Найти производную функции: .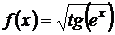

Решение. Преобразуем функцию 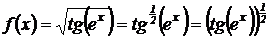. Тогда: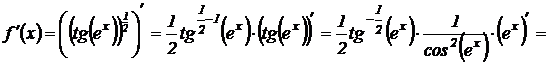

.

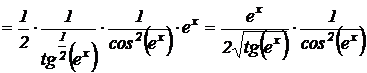Пример 1.8. Вычислить 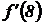, если .

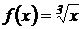Решение. Найдем 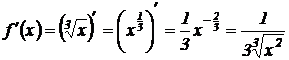. Вычислим .

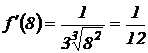Примеры для самостоятельного решения

Вычислить пределы:

1. .

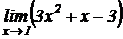2. .

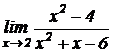3. .

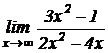4. .

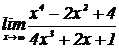5.

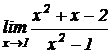
Найти производные функций:

1. .

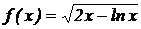2.

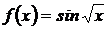
3. .

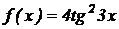4. .

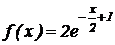5. .

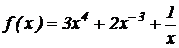6. .

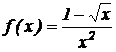7. .

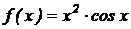8. .

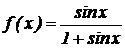Задание на дом

Практика:

Найти пределы функций:

1. .

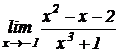2. .

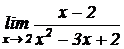3. .

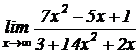4. .

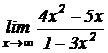Найти производные функций:

1. .

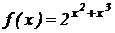2. .

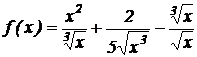3. .

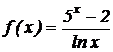4. .

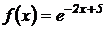5. .

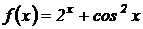6. .

7. .

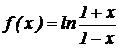8. .

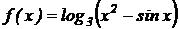Теория:

1. Лекция по теме «Дифференциал функции. Производные и дифференциалы высших порядков. Применение производных к решению прикладных задач».

2. Занятие 2 данного методического пособия.

3. Павлушков И.В. и другие стр. 65-100.

Производные высших порядков

Производная 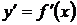функции есть также функция от хи называется производной первого порядка.

Если функция 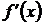дифференцируема, то ее производная называется производной второго порядка и обозначается 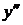или 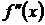. Итак, .

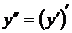Производной n–го порядка или n-ой производной называется производная от производной (n-1) порядка: 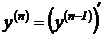.Производные порядка выше первого называются производными высших порядков.

Приложение дифференциального исчисления

Функция называется возрастающей (убывающей) на интервале (a; b), если для любых двух точек x₁ и x₂ из указанного интервала, удовлетворяющих неравенству 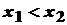, выполняется неравенство ( ).

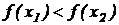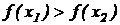Необходимое условие возрастания (убывания): Если дифференцируемая функция на интервале (a, b) возрастает (убывает), то производная этой функции неотрицательна (неположительна) в этом интервале ( ).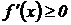

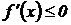Достаточное условие возрастания (убывания):Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого интервала, то функция возрастает (убывает) на этом интервале.

Функция f(x)в точке х₁имеет максимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x₁)>f(x), при x¹x₁.

Функция f(x) в точке х₁ имеет минимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x₁)<f(x), при x¹x₁.

Экстремум функции называют локальным экстремумом, так как понятие экстремума связано лишь с достаточно малой окрестностью точки х₁. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой. Наличие максимума или минимума в отдельной точке интервала не означает, что в этой точке функция f(x) принимает наибольшее или наименьшее значение на этом интервале.

Необходимое условие экстремума: В точке экстремума дифференцируемой функции ее производная равна нулю.

Достаточное условие экстремума: Если производная дифференцируемой функция в некоторой точке х₀ равна нулю и меняет свой знак при переходе через это значение, то число f(х₀) является экстремумом функции, причем если изменение знака происходит с плюса на минус, то максимум, если с минуса на плюс, то минимум.

Точки, в которых производная непрерывной функции равна нулю или не существует называются критическими.

Исследовать функцию на экстремум означает найти все ее экстремумы. Правило исследования функции на экстремум:

1). Найти критические точки функции у = f(x) и выбрать из них лишь те, которые являются внутренними точками области определения функции;

2). Исследовать знак производной f'(x) слева и справа от каждой из выбранных критических точек;

3). На основании достаточного условия экстремума выписать точки экстремума (если они есть) и вычислить значения функции в них.

Для того чтобы найти наибольшее и наименьшее значение функции на отрезке необходимо выполнить несколько этапов:

1). Найти критические токи функции, решив уравнение f’(x)=0.

2). Если критические точки попали на отрезок, то необходимо найти значения в критических точках и на границах интервала. Если критические точки не попали на отрезок (или их не существует), то находят значения функции только на границах отрезка.

3). Из полученных значений функции выбирают наибольшее и наименьшее и записывают ответ, например, в виде: ; .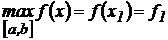

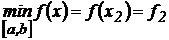Решение задач

Пример 2.1. Найти дифференциал функции: .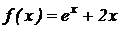

Решение. На основании свойства 2 дифференциала функции и определения дифференциала имеем:

.

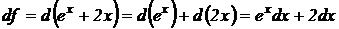Пример 2.2. Найти дифференциал функции: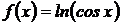

Решение. Функцию можно записать в виде: 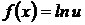, 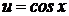. Тогда имеем:

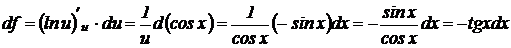
Пример 2.3. Найти вторую производную функции: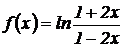

Решение. Преобразуем функцию .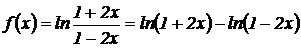

Найдем первую производную: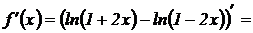

;

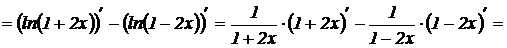
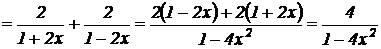найдем вторую производную:

.

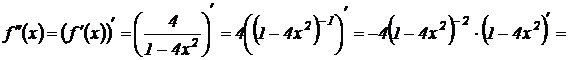
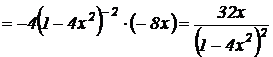Пример 2.4. Найти дифференциал второго порядка от функции .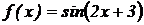

Решение. Найдем дифференциал второго порядка на основании выражения для вычисления :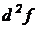

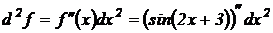. Найдем сначала первую производную:

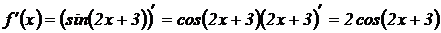; найдем вторую производную: .

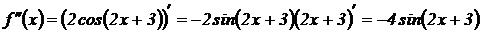Тогда .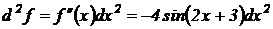

Пример 2.5. Найти угловой коэффициент касательной к кривой 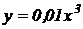, проведенной в точке с абсциссой х=2.

Решение. На основании геометрического смысла производной имеем, что угловой коэффициент равен производной функции в точке, абсцисса которой равна х. Найдем .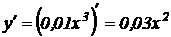

Вычислим 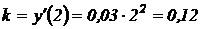– угловой коэффициент касательной к графику функции.

Пример 2.6. Популяция бактерий в момент времени t (t измеряется в часах) насчитывает 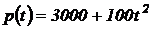особей. Найти скорость роста бактерий. Найти скорость роста бактерий в момент времени t = 5 часов.

Решение.Скорость роста популяции бактерий – это первая производная 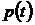по времени t: .

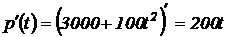Если t = 5 часов, то 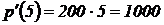. Следовательно, скорость роста бактерий составит 1000 особей в час.

Пример 2.7. Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, уменьшении температуры тела, изменении пульса или других физиологических показателей. Степень реакции зависит от назначенной дозы лекарства. Если х обозначает дозу назначенного лекарства, а степень реакции у описывается функцией 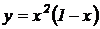. При каком значении х реакция максимальна?

Решение. Найдем производную .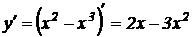

Найдем критические точки: 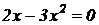⇒ 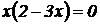. ⇒ Следовательно, имеем две критические точки: 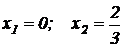. Значение 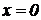не удовлетворяет условию задачи.

Найдем вторую производную 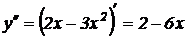. Вычислим значение второй производной при 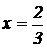. . 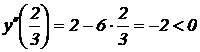Значит, 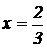– уровень дозы, который дает максимальную реакцию.

Примеры для самостоятельного решения

Найти дифференциал функции:

1. .

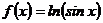2. .

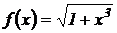3. .

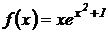4.

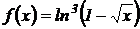
Найти вторые производные следующих функций:

5. .

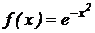6. .

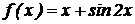7. .

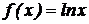8. .

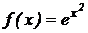Найти производные второго порядка и записать дифференциалы второго порядка для следующих функции:

9. .

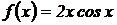10. .

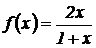11. Исследовать функцию на экстремум .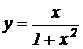

12. Найти наибольшее и наименьшее значения функции 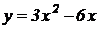на отрезке .

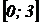13. Найти интервалы возрастания и убывания функции, точки максимума и минимума и точки пересечения с осями: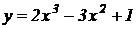

14. Закон движения точки имеет вид 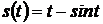. Определить закон скорость и ускорение этой точки.

15. Уравнение движения точки имеет вид 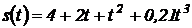(м). Найти 1) положение точки в моменты времен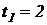и с и 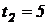с; 2) среднюю скорость за время, прошедшее между этими моментами времени; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.

Задание на дом.

Практика:

Найти дифференциал функции:

1. ;

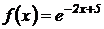2. ;

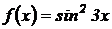Найти производные второго порядка функции:

3. .

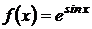4.

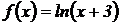
5.

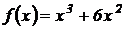
Найти дифференциалы второго порядка

6. .

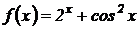7. Точка движется прямолинейно по закону 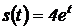. Вычислить скорость и ускорение в моменты времен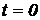и и .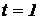

Найти интервалы возрастания и убывания функций:

8. .

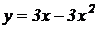9. .

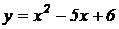10. При вливании глюкозы ее содержание в крови человека, выраженное в соответствующих единицах, спустя t часов составит 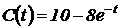. Найдите скорость изменения содержания глюкозы в крови при а) t =1 ч; б) t =2 ч.

Теория.

1. Лекция по теме «Производные и дифференциалы функции нескольких аргументов. Приложение дифференциала функции нескольких аргументов».

2. Занятие 3 данного методического пособия.

3. Павлушков И.В. и другие стр. 101-113, 118-121.

Занятие 3. Производные и дифференциалы функции нескольких аргументов

Актуальность темы: данный раздел математики имеет широкое применение при решении ряда прикладных задач, так как многим явлениям физического, биологического, химического явления присуща зависимость не от одной, а от нескольких переменных (факторов).

Цель занятия: научиться находить частные производные и дифференциалы функций нескольких переменных.

Целевые задачи:

знать: понятие функции двух переменных; понятие частных производных функции двух переменных; понятие полного и частных дифференциалов функции нескольких переменных;

уметь: находить производные и дифференциалы функций нескольких переменных.

Краткие сведения из теоретического курса

Основные понятия

Переменная z называется функцией двух аргументов x и y, если некоторым парам значений 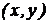по какому-либо правилу или закону ставится в соответствие определенное значение z. Функция двух аргументов обозначается .

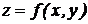Функция 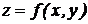задается в виде поверхности в прямоугольной системе координат в пространстве. Графиком функции двух переменных 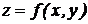называется множество точек трехмерного пространства (x, y, z), аппликата z которых связана с абсциссой хи ординатой у функциональным соотношением .

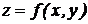Рассмотрим функцию z=f(x,y). Дадим аргументу х приращение Dх, а аргументу у – приращение Dу. Тогда функция z получит наращенное значение .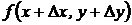

Величина 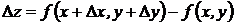называется полным приращением функции в точке 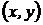. Частным приращением по переменной х называется величина: 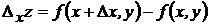. Аналогично определяется частное приращение по переменной у: .

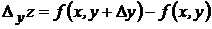Частные производные и дифференциалы функции
нескольких переменных

Частной производной от функции 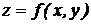по независимой переменной х называют конечный предел 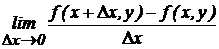, вычисленный при постоянном у. Обозначается: 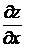или .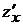

Частной производной от функции 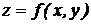по независимой переменной у называют конечный предел 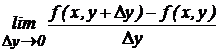, вычисленный при постоянном х. Обозначается: 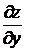или .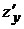

Пусть функция z=f(x,y) имеет две непрерывные частные производные .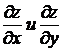

Произведение 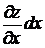называется частным дифференциалом функции z=f(x,y) по х и обозначаются .

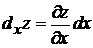Произведение 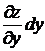называется частным дифференциалом функции z=f(x,y)по хи обозначаются .

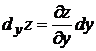Полный дифференциал функции

Дифференциалом функции называется сумма произведений частных производных этой функции на приращение соответствующих независимых переменных, т. е. 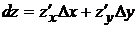. Так как 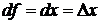и 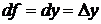тогда можно записать: 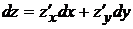или .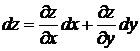

Решение задач

Пример 3.1. Найти частные производные функций:

1). ;

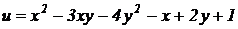2). .

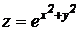Решение. 1) рассматривая у как постоянную величину, получим 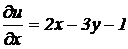, рассматривая х как постоянную величину, найдем: .

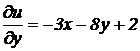2) пусть 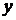– const, получим ,

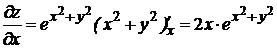пусть х – const, получим .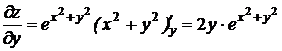

Пример 3.2. Реакция на инъекцию х единиц лекарственного препарата описывается функцией 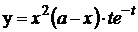, где t выражается в часах с момента инъекции, a – некоторая константа. Найти частные производные .

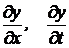Решение. Найдем частные производные

;

.

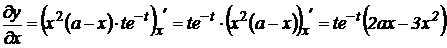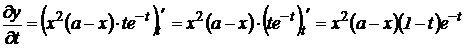Пример 3.3. Для функции 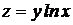найти производные второго порядка.

Решение. Найдем частные производные первого порядка , .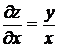

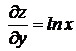Дифференцируя повторно, получим:

.

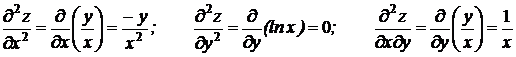Пример 3.4. Найти полный дифференциал функций:

1). ;

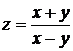2). .

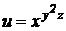Решение. 1) Найдем частные производные

;

.

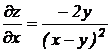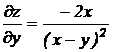Следовательно, .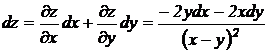

2) найдем частные производные по переменным х, у и z:

, , ,

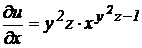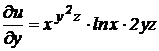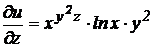следовательно

.

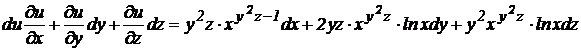Примеры для самостоятельного решения

Найти частные производные функций:

1. .

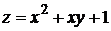2. .

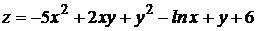3. .

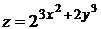4. .

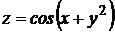Найти все частные производные второго порядка функции:

5. .

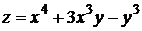6. .

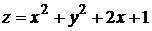Найти частные и полный дифференциал для следующих функций:

7. .

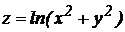8. .

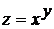9. .

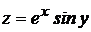10. .

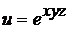Задание на дом

Практика

Найти все частные производные функций:

1. .

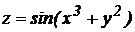2. .

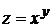3. .

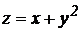4. .

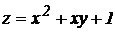Найти частные и полный дифференциал для следующих функций:

5. .

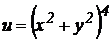6. .

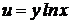7. .

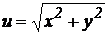8. .

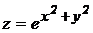Теория

1. Лекция по теме «Неопределенный интег