Марковский случайный процесс в СМО

Процессы поступления и обслуживания заявок в СМО являются случайными, что обусловлено случайным характером потока заявок и длительности их обслуживания.

Случайным процессом X(t) называется процесс, значение которого при любом значении аргумента t является случайной величиной. При фиксированном t=t₀ X(t₀) представляет собой обычную величину. Случайные процессы упрощают исследование СМО.

По характеру потоков событий СМО разделяются на марковские и немарковские. В дальнейшем мы будем иметь дело с системами первого типа. Преимущества и полезность такого подхода состоят в том, что для выработки основных рекомендаций нужно знать не точные характеристики СМО, а лишь их приближенные значения. В основе СМО будем предполагать марковский случайный процесс (процесс без последствия), когда вероятность состояния СМО в будущем зависит только от ее состояния в настоящем и не зависит от прошлого (название по имени известного российского математика А.А.Маркова). Условие марковского случайного процесса: необходимо, чтобы все потоки событий, при которых система переходит из одного состояния в другое (потоки заявок, потоки обслуживания и т.д.) были пуассоновскими.

Пуассоновский поток событий обладает следующими свойствами:

— отсутствия последствия (число событий, попавших на заданный временной интервал, не зависит от числа событий, попавших на другие интервалы);

— ординарности (вероятность попадания на элементарный временной интервал двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события);

— стационарности (число событий, попавших на заданный временной интервал зависит лишь от длины интервала и не зависит от числа событий, попавших на другие интервалы).

Известно, что для простейшего потока, т.е. обладающего вышеперечисленными свойствами, справедлив закон Пуассона. Плотность вероятности случайной величины при этом:

,

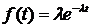где λ – интенсивность потока.

Уравнения Колмогорова

При анализе случайных процессов с дискретными состояниями пользуются графом состояний, где прямоугольниками изображают состояния системы, а переходы из состояния в состояние – стрелками. Если у стрелок проставлены интенсивности, то граф состояния называется размеченным. Переходы системы из состояния S_i в состояние S_j происходят под воздействием простейших потоков событий с интенсивностями λ_ij.

Простейший граф состояний представлен на рис.1.

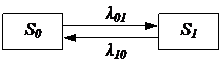
Рис. 1

На рис. 1 изображена СМО, состоящая из одного телефонного аппарата, который находится в двух возможных состояниях: либо свободен (S₀), либо занят (S₁); λ₀₁ – интенсивность нагрузки аппарата, или количество заявок на переговоры в единицу времени; λ₁₀ – интенсивность обслуживания аппаратом, или количество обслуживаемых заявок в единицу времени.

Стрелка из S₀ в S₁ означает переход системы из состояния «аппарат свободен» в состояние «аппарат занят». Стрелка из S₁ в S₀ означает обратный переход.

Анализ состояния СМО сводится к определению вероятности, с которой система пребывает в данном состоянии.

В общем случае вероятностью i-го состояния p_i(t) называется вероятность того, что в момент t система будет находиться в состоянии S_i.

Для любого момента t справедливо соотношение:

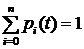, (5)

где n+1 – общее число состояний СМО.

Определить вероятности состояний СМО можно, решив систему уравнений Колмогорова.

Алгоритм составления системы уравнений Колмогорова:

1. В левую часть каждого уравнения ставится производная вероятности i-го состояния по времени.

2. В правую часть каждого управления ставится:

а) сумма произведений вероятностей всех состояний, из которых идут стрелки в i-е состояние, на интенсивности соответствующих потоков событий;

б) минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность i-го состояния.

В полученной системе Колмогорова независимых уравнений на единицу меньше их общего числа. Для решения системы добавим уравнение (5).

Задав начальные условия и решив систему дифференциальных уравнений Колмогорова, находят систему функций времени p_i(t), где i – номер состояния. Это позволяет получить дискретное распределение вероятностей СМО для любого момента времени. Для достаточно большого значения времени t независимо от начальных условий распределение вероятностей стабилизируется и практически не зависит от времени.