Дифференциальные уравнения первого порядка в нормальной и

Диффернциальной форме

Уравнения с разделяющимися переменными

Определение 12.8.

Пусть в уравнении 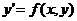функция 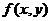может быть разложена на множители, каждый из которых зависит только от одной переменной, то есть 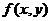= 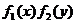или в уравнении M(x,y)dx+N(x,y)dy=0 коэффициенты имеют вид

M(x,y)=M₁(x)M₂(y); N(x,y)=N₁(x)N₂(y).

Тогда такие дифференциальные уравнения называются уравнениями с разделяющимися переменными.

Путем деления на f₂(y) и на M₂(y)N₁(x) эти уравнения приводятся соответственно к виду .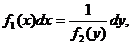

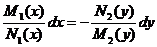Также дифференциальные уравнения называются уравнениями с разделенными переменными.

Теорема 12.2.

Общим интегралом дифференциального уравнения с разделёнными переменными X(x)dx+Y(y)dy=0 является выражение .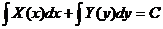

Пример 12.3.

Решим дифференциальное уравнение .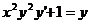

Приведём уравнение к виду 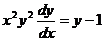или .

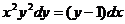Деля обе части на 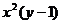, приходим к уравнению с разделенными переменными 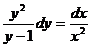. Интегриря обе части уравнения, получим 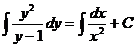, откуда .

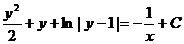При делении на 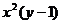могли быть потеряны решения x≡0 и y≡1. Очевидно, что y≡1 является решением уравнения, а x≡0 – нет.

Пример 12.4

Найдем частное решение дифференциальное уравнения ,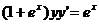

удовлетворяющее условию y(0)=1.

Имеем .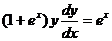

Разделяя переменные, получим 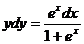, откуда .

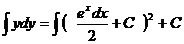Интегрируя, находим общий интеграл 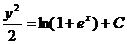. Полагая в нём x=0, y=0, будем иметь 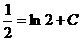, откуда C = 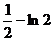. Подставляя в общий интеграл найденное значение С, получим частное решение 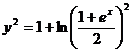, или .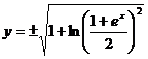

Из начального условия следует, что y>0, (y(0)=1>0), поэтому перед корнем берем знак плюс, а значит, искомое частное решение .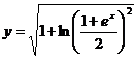

Пример 12.5.

Проинтегрируем дифференциальное уравнение 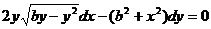и выделим интегральную кривую, проходящую через точку (0;b).

Разделяем переменные в уравнении, тогда получим 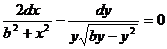, откуда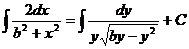

1) при 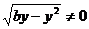, имеем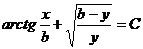

2) при 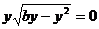находим решения уравнения: 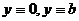. Первое из этих решений частное, второе – особое.

Прежде чем выделить интегральную кривую, проходящую через заданную точку (0,b), заметим, что через эту точку проходит особое решение 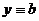, так что в ней нарушается единственность решения.

Полагая в общем интеграле 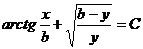x=0, y=b,находим С=0, так что через заданную точку проходит две интегральных кривых 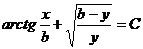и .

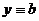Однородные дифференциальные уравнения и приводящиеся к ним

Определение 12.9.

Однородной функцией m измеренияназывается функция 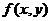, для которой верно равенство .

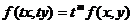Определение 12.10.

Дифференциальные уравнения 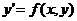называются однородными, если 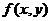есть однородная функция нулевого измерения, то есть .

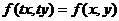Однородное уравнение всегда можно представить в виде .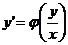

Любой из подстановок 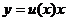или 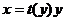однородное уравнение сводится к уравнению с разделяющимися переменными.

Например, вводя новую искомую функцию 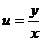можно свести уравнение 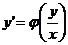к уравнению 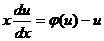, в котором переменные разделяются.

Если u≡u₀, есть корень уравнеия 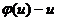= 0, то решением однородного уравнения будет u≡u₀, или y=u₀x.

Пример 12.6.

Решим дифференциальное уравнение .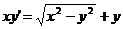

Имеем однородное уравнение (заменяя в уравнении x и y на tx, ty, приходим к однородному уравнению).

Данное уравнение приводится к виду .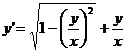

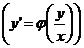Положим 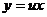, тогда 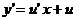, откуда .

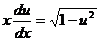Разделим переменные: 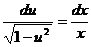. Интегрированием функций находим 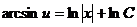или 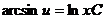. Подставляя 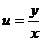, после преобразования получим общее решение .

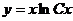При разделении переменных обе части уравнения делили на произведение 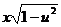, поэтому могли потерять решения, которые обращают в нуль это произведение.

Пример 12.7.

Проинтегрируем дифференциальное уравнение 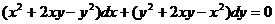и выделим интегральные кривые, проходящую через точки: а) (2;2); б) (1;-1).

Положим 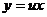, тогда 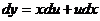, так что

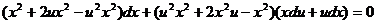. Разделим переменные: 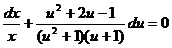, (u + 1 ≠ 0).

Интегрируя, получим 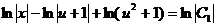или .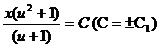

Заменив 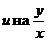, получим общий интеграл уравнения в виде 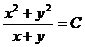(семейство окружностей ).

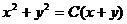При u+1 = 0 имеем 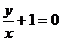(особое решение).

Решим поставленные задачи Коши:

а) полагая в 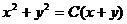x=2, y=2, находим С=2, так что искомое решение: .

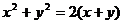б) ни одна из окружностей 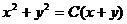не проходит через точку (1;-1), зато полупрямая 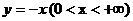проходящая через эту точку и дает искомое решение.

Дифференциальные уравнения вида 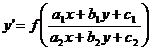в случае 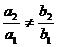приводится к однородным уравнениям с помощью замены переменных x=u+m, y=v+n, где m и n находятся из системы уравнений a₁m+b₁n+c₁=0, a₂m+b₂n+c₂=0.

Если в данном уравнении 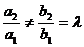и, следовательно, a₂x+b₂y=λ(a₁x+b₁y), то оно примет вид .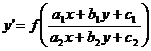

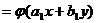Подстановкой 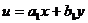это уравнение преобразуется к уравнению с разделяющимися переменными.

Пример 12.8.

Решим уравнение .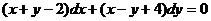

Система m+n-2=0; m-n+4=0 имеет единственное решение m=-1, n=3. Замена x=u-1, y=v+3 приводит данное уравнение к виду 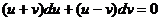, которое является однородным уравнением.

Полагая 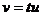, получим 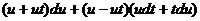, откуда .

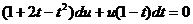Разделим переменные: 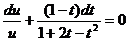. Интегрируя, находим 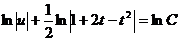или .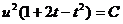

Возвращаясь к старым переменным x и y, получим 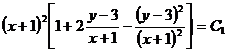или .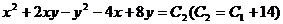

Пример 12.9.

Решим дифференциальное уравнение .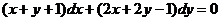

Система m+n+1=0; 2m-2n-1=0 несовместна. Для интегрирования уравнения применяем подстановку 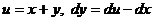, после чего уравнение принимает вид

.

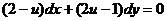Разделяя переменные, получим 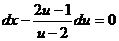, откуда . Возвращаясь к переменным x, y получим общий интеграл данного уравнения

.
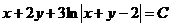