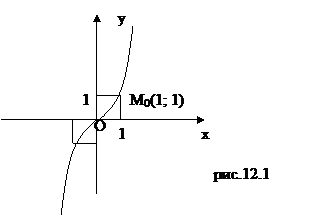Дифференциальные уравнения первого порядка. Классификация решений

Отметим записи дифференциального уравнения первого порядка:

1) 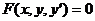- уравнение в общем виде:

2) 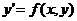- уравнение в нормальной форме:

3) M(x,y)dx+N(x,y)dy=0 - уравнение в дифференцированной форме.

Наряду с уравнением 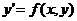также будет рассматриваться «перевернутое» уравнение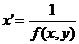

Пример 12.1.

Решим дифференциальное уравнение .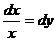

Имеем 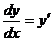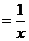, откуда y=ln|x|+C.

К решениям y=ln|x|+C уравнения 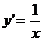следует присоединить решение x≡0 “перевернутого уравнения”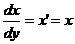

Определение 12.4.

Задачей Коши называют задачу нахождения решения 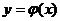дифференциального уравнения 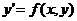, удовлетворяющего начальному условию y(x₀)=y₀. Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку M₀(x₀,y₀) плоскости xОy.

Теорема 12.1(о существовании и единственности решения задачи коши.)

Пусть в уравнении 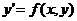функция 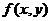определена в некоторой области D плоскости xОy, содержащей точку M₀(x₀,y₀).

Задача Коши имеет решение и притом единственное на некотором интервале 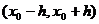, если функция f(x,y) и её частная производная 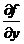непрерывны в области D.

Определение 12.5.

Решение y=φ(x,C) уравнения 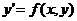, где функция φ(x,C) определена в некоторой области изменения переменных х и С и имеет непрерывную частную производную по х, называется общим решением данного уравнения в заданной области D изменения переменных х и y, если в каждой точке этой области решения задачи Коши существует и единственно.

Иначе, общее решение 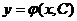уравнение 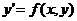это:

1)решение данного уравнения;

2)какие бы начальные условия y(x₀)=y₀ ни задать, существует параметр C

такой, что эти начальные условия будут удовлетворены (т. е. уравнение 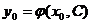разрешимо относительно С).

Замечание 12.1.

Если общее решение уравнения 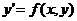задано в неявном виде 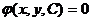, то оно называется общим интеграломэтого уравнения.

Определение 12.6.

Решение, в каждой точке которого сохраняется единственность решения задачи Коши, называется частным решением.

Частное решение получается из общего решения при конкретном значении параметра С.

Определение 12.7.

Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением.

Особое решение всегда можно обнаружить в процессе построения общего решения данного дифференциального уравнения. Это те решения, которые могут быть утеряны при преобразовании данного уравнения в процессе решения.

Пример 12.2.

Покажем, что функция 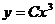является решением дифференциального уравнения 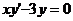и найдем частное решение, удовлетворяющее условию 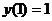(т. е. найдем интегральную кривую, проходящую через данную точку M₀(1;1)).

Имеем 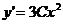. Подставляя y и 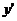в уравнение, получаем тождество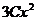 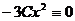. Это означает, что функция 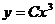является решением данного дифференциального уравнения. Положив в нем , , 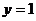найдем значение параметра 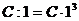откуда 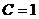. Подставив 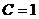в решение, получим частное решение .

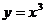Интегральной кривой, проходящей через точку M₀(1;1) является кубическая парабола 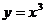(рис. 12.1).