Направление выпуклости кривой

Определение 4.2.

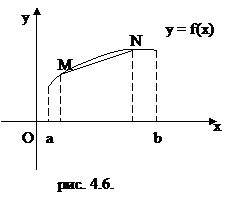
Пусть функция f(x) непрерывна на интервале (a, b). Кривая у = f(x) называется выпуклой вверх (вниз) на (a, b), если для любых двух точек M и N на этой кривой, абсциссы которых принадлежат интервалу (a, b), соединяющая их хорда лежит ниже (выше) кривой.

На рис. 4.6 кривая у = f(x) выпукла вверх, а на рис. 4.7 – вниз.

Замечание 4.5.

Если функция f(x) дифференцируема на интервале (a, b), то она называется выпуклой вверх (вниз) на (a, b), если касательная, проведенная в любой точке М кривой с абсциссой из (a, b), лежит выше (ниже) кривой, кроме точки касания.

На рис. 4.8 кривая y = f(x) выпукла вверх, а на рис. 4.9 – вниз.

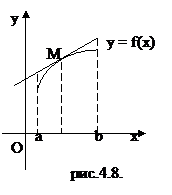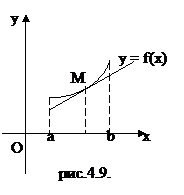Теорема 4.10 (о необходимом условии выпуклости кривой).

Предположим, что функция f(x) дважды дифференцируема на интервале (a,b), тогда если кривая y = f(x) выпукла вверх (вниз) на (a, b), то f''(x) ≤ 0 (f''(x) ≥ 0) при всех х (a, b).

Теорема 4.11 (о достаточном условии выпуклости кривой).

Пусть функция f(x) дважды дифференцируема на интервале (a, b), тогда если f''(x) < 0 (f''(x) > 0) при всех х (a, b), кроме возможно конечного числа точек, в которых f''(x) = 0, то кривая y = f(x) выпукла вверх (вниз) на (a, b).

Пример 4.8.

Определим интервалы постоянной выпуклости кривой у = f(x) = 2х + 3 .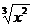

Вычислим вторую производную: 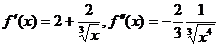. Нетрудно видеть, что f''(x) < 0при х (-∞, 0) 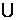(0, +∞).

Следовательно, по теореме 4.11 исходная кривая является выпуклой вверх на промежутках (-∞, 0) и (0, +∞), что и отражено на рис. 4.5.

Точки перегиба кривой

Определение 4.3.

Предположим, что функция f(x) непрерывна на интервале (a, b) и х₀ (a, b).

Точка М₀ (х₀, f(x₀)) называется точкой перегиба кривой y = f(x), если при переходе через эту точку кривая y = f(x) меняет направление выпуклости.

Точка перегиба является локальной характеристикой и дает представление о поведении кривой лишь в некоторой окрестности х₀.

На рис 4.10 и 4.11 точка М₀ является точкой перегиба изображенных кривых.

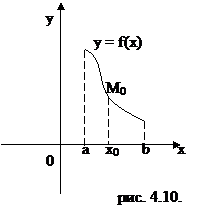Теорема 4.12(о необходимом условии перегиба кривой).

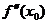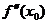Если точка М₀(х₀,f(x₀)) является точкой перегиба кривой y=f(x) и существует , то =0.

Следствие

Если точка М₀(х₀,f(x₀)) есть точка перегиба кривой y=f(x), то либо 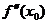=0, либо 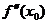не существует.

Точка М₀(х₀,f(x₀)) называется точкой, подозрительной на перегиб, если для абсциссы этой точки выполняется одно из условий следствия.

Теорема 4.13(о достаточном условии перегиба кривой).

Пусть функция f(x) дважды дифференцирована в некоторой окрестности точки x₀ за исключением возможно самой точки x₀, а в точке x₀ функция f(x) непрерывна, тогда если 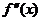меняет знак при переходе через x₀, то точка М₀(х₀,f(x₀)) является точкой перегиба кривой y=f(x).

Пример 4.9.

Определим точки перегиба кривой .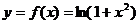

Вычислим вторую производную и найдем точки, подозрительные на перегиб: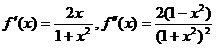

Вторая производная существует при всех 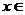/R и обращается в нуль при x₁=-1 и x₂=1.

Таким образом, точки М₁(-1, ln2), М₂(1, ln2) являются точками, подозрительными на перегиб.

Составим следующую таблицу:

X	(-∞,-1)	-1	(-1,1)		(1,+∞)
Знак f''(x)	-		+		-

у

Как видно из таблицы, f''(x) меняет знак при переходе через точки x₁=-1 и x₂=1. Согласно теореме 4.13 точки М₁(-1, ln2) и М₂(1, ln2) есть точки перегиба исходной кривой (рис.4.12).

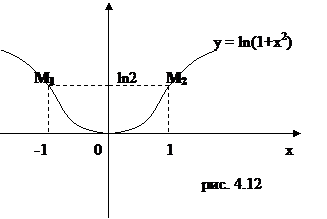
Построение графика функции

При исследовании функции и построении ее графика целесообразно придерживаться следующей схемы:

1. Исследование функции без использования первой и второй производных.

а) Найти область определения функции D(f).

б) Определить точки пересечения графика с осями Ох и Оу.

в) Проверить, является ли функция четной, нечетной или периодической.

г) Выяснить вопрос о существовании вертикальных и наклонных асимптот (см. п. 2.7).

2. Исследование функции с помощью первой производной.

а) Найти точки, подозрительные на экстремум.

б) Заполнить таблицу интервалов постоянной монотонности и точек экстремума.

3. Исследование функции с помощью второй производной.

а) Найти абсциссы точек, подозрительных на перегиб.

б) Заполнить таблицу интервалов постоянной выпуклости и точек перегиба.

4. Построение графика функции в целом.

Пример 4.10.

Построить график функции f(x) = .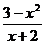

Будем следовать изложенной выше схеме.

1. Область определения функции есть множество D(f) = (-∞, -2) 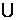(-2, +∞).

Определим точки пересечения графика функции с осями Ох, Оу: А( 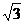, 0); В(- 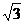, 0); С(0, ).

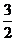Отметим, что функция не является ни четной, ни нечетной, а также не является периодической.

Вычислим односторонние пределы в точке х=-2: .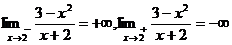

Следовательно, прямая х = -2 является вертикальной асимптотой.

Исследуем наличие наклонных асимптот. Пусть х→ +∞, тогда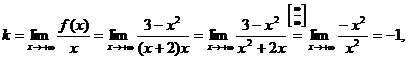

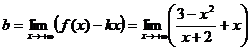
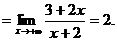
Следовательно, прямая у = -х+2 есть наклонная асимптота при х→ +∞.

Аналогично доказывается, что та же прямая является наклонной асимптотой при х→ -∞.

2. Для определения точек, подозрительных на экстремум, вычислим производную .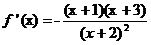

Точками подозрительными на экстремум, будут точки х₁ = 3 и х₂ = -1, в которых производная обращается в нуль.

Заполним таблицу интервалов постоянной монотонности и точек экстремума:

х	(-∞, -3)	-3	(-3, -2)	(-2, -1)	-1	(-1, +∞)
знак f'(x)	-		+	+		-
Возрастание, убывание; вид экстремума		min			max

Из таблицы видно, что х₁ = х_min = -3, при этом у_min = f(x_min) = 6, а х₂ = х_max = -1, при этом у_max = f(x_max) = 2.

Отметим также, что функция убывает на промежутке (-∞, -3), (-1, +∞) и возрастает на промежутках (-3, -2), (-2, -1).

Для нахождения точек, подозрительных на перегиб, вычислим вторую производную f''(x) = - .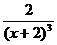

Подозрительной на перегиб является единственная точка с абсциссой х = -2, но поскольку точка х = -2 не принадлежит области определения функции, то перегибов график функции не имеет.

Заполним таблицу интервалов постоянной выпуклости:

х	(-∞, -2)	(-2, +∞)
знак f''(x)	+	-
Направление выпуклости

Из таблицы видно, что на промежутке (-∞, -2) кривая у = f(x) выпукла вниз, а на промежутке (-2, +∞) – выпукла вверх.

4. Строим график функции (рис. 4.13).