Тема 2.1.Случайные события. Классическое
МАТЕМАТИКА
Контрольные задания для студентов-заочников
Специальностей
«Экономика и бухгалтерский учёт»
Г. Алатырь, 2010 г.
| РАССМОТРЕНО предметной комиссией гуманитарных и естественнонаучных дисциплин Протокол № _____ от «____»_______ 2010 г. Председатель _________________________ |
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Данное пособие ставит своей целью оказание помощи студентам заочного отделения средних специальных учебных заведений в организации их самостоятельной работы по овладению системой знаний, умений и навыков в объеме программы.
Эта работа требует не только большого упорства, но и умения, без которого затрата сил и времени не дает должного эффекта. Читать, понимать прочитанное и применять его практически – вот в чем суть умения работы с учебным пособием.
Прежде всего, необходимо ознакомиться с содержанием программы. Затем выбрать в качестве основного учебное пособие и придерживаться его при изучении всего курса, так как замена учебника может привести к утрате логической связи между отдельными вопросами. Помните: учебник нужно не просто читать, а изучать, основой запоминания является понимание, знание забывается – понимание никогда; повторение – важнейшее средство, предотвращающее забывание, необходимо выработать привычку систематически самостоятельно работать, «натаскивание» к экзамену дает слабые и поверхностные знания. Решение примеров является лучшим способом закрепления материала.
Контрольные работы следует выполнять самостоятельно и лишь после того, как проработали соответствующий материал, и решили необходимый минимум задач.
Так как каждой теме соответствует задача или упражнение, то контрольную работу следует выполнять постепенно по мере изучения материала.
При решении задач следует обосновывать каждый шаг решения, исходя из теоретических основ курса. Не следует применять формулы, которые не входят в программу. Решение должно быть доведено до окончательного ответа.
ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3см для замечаний преподавателя. На обложке тетради должен быть приклеен титульный лист утвержденного образца или аккуратно записаны все данные титульного листа: шифр, специальность, фамилия, имя, отчество учащегося предмет и номер варианта работы.
Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.
Каждую задачу нужно начинать с новой страницы.
Условия задачи должны быть обязательно переписаны полностью в контрольную тетрадь, к геометрическим задачам, кроме того, дается установленная краткая запись условия.
Решения задач должны сопровождаться краткими но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.
В конце работы следует указать литературу, которой вы пользовались. Если в работе допущены недочёты и ошибки, то студент должен выполнить все указания преподавателя, сделанные в рецензии.
Контрольная работа должна быть выполнена в срок (в соответствии с учебным планом, графиком).
В период сессии работы на проверку не принимаются.
ТЕМАТИЧЕСКИЙ ПЛАН ДИСЦИПЛИНЫ
| Наименование разделов и тем | Количество часов | |
| Всего | Практических | |
| Раздел 1. Элементы теории вероятностей | ||
| Тема 1.1 Основные понятия комбинаторики | ||
| Тема 1.2 Случайные события вероятность событий | ||
| Раздел 2. Дифференциальное исчисление | ||
| Тема 2.1. Производные функции | ||
| Тема 2.2. Исследование функции с помощью производной | ||
| Раздел 3. Интегральное исчисление | ||
| Тема 3.1 Неопределенный интеграл | ||
| Тема 3.2. Определенный интеграл | ||
| Раздел 4. Дифференциальные уравнения | ||
| Тема 4.1 Дифференциальные уравнения |
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
& Введение
Студент должен:
Иметь представление:
- о роли и месте знаний по дисциплине в процессе освоения основной профессиональной образовательной программы по специальности.
Предмет и задачи курса. Математика и научно – технический процесс. Применение математики в экономике, производстве. Математика и современная вычислительная техника, программирование экономическая информация.
Роль математики и математических знаний в подготовке специалистов избранной профессии.
& Раздел 1. Элементы теории вероятностей
Тема 1.1 Основные понятия комбинаторики
Студент должен:
Знать:
- основные комбинаторные объекты (типы выборок);
- формулы и правила расчёта количества выборок (для каждого из типа выборок)
Уметь:
- определить тип комбинаторного объекта (тип выборки);
- рассчитывать количество выборок заданных условиях.
Упорядоченные выборки (размещения). Правило произведения. Размещение с повторениями. Размещение без повторений. Перестановки. Размещения с заданным количеством повторений каждого элемента. Неупорядоченные выборки (сочетания). Сочетания без повторений. Сочетания с повторениями.
Определение вероятностей
Студент должен:
иметь представление:
- о видах текстовых редакторов и их возможностях;
знать:
- понятие случайного события, понятия совместимых и несовместимых событий;
- классическое определение вероятности;
- методику вычисления вероятностей событий по классической формуле определения вероятности с использованием элементов комбинаторики;
уметь:
-вычислять вероятности событий по классической формуле определения вероятности;
Понятие случайного события. Совместимые и несовместимые события. Полная группа событий. Равновозможные события . Общее понятие о вероятности события как о мере возможности его наступления. Классическое определение вероятности.
& Раздел 2. Дифференциальное вычисление
Производной
Студент должен:
Иметь представление:
- об общей схеме исследования функции и построении ее графика:
Знать:
- определение точки перегиба:
- определение асимптот графика функции:
- общую схему исследования функции
Уметь:
- применять вторую производную для нахождения точек перегиба функции:
- устанавливать направления выпуклости графика функции
- находить асимптоты графика функции
- исследовать функцию по общей схеме и строить ее график
Применение второй производной. Асимптоты графика функции. Направление выпуклости графика функции. Точки перегиба. Общая схема исследования функции.
& Раздел 3. Интегральное исчисление
ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА
Вариант 1
1. В вазе 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее 4 красных и 3 розовых гвоздики?
2. Найти производную функции: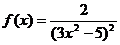 
3. Исследовать функцию: у = х3 – 12х + 4 и построить график
4. Резервуар ёмкостью 108 м3 с квадратным основанием, открытый сверху, нужно покрыть (с внешней стороны) эмалью. Каковы должны быть размеры резервуара, чтобы израсходовать для этого минимальное количество эмали?
5. Вычислить интегралы:
а)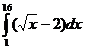 
б) 
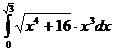
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = 8х – х2 – 7 и осью Ох
7. Решить дифференциальное уравнение: (1+у)dx – (1 – х)dу = 0
Вариант 2
1. В борьбе за призовые места на студенческой олимпиаде по информационным технологиям участвуют 16 команд. Сколькими способами можно распределить три призовых места между ними?
2. Найти производную функции: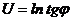 
и вычислить U' 
3. Исследовать функцию: у = х3+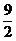 
х2+6х+2 и построить график
4. Тело движется прямолинейно по закону S = 2 + 12t +2t2 –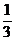 
t3. Найти максимальную скорость движения тела.
5. Вычислить интегралы:
а)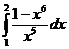 
б)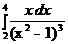 
6. Сделать чертеж и вычислить площадь фигуры, ограниченной линиями: у = х3 –1 у = 0, х = 0
7. Решить дифференциальное уравнение: ех(1+еу)dx+еу(1+ех)dу=0
Вариант 3
1. Для некоторой местности в июле шесть пасмурных дней. Найти вероятность, того что:
а) первого и второго июля будет ясная погода;
б) первого и второго июня будет ясная погода, а третьего июня - пасмурная.
2. Найти производную функции: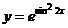 
и вычислить у' 
3. Исследовать функцию: у = х3 –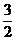 
х2 – 6х + 1 и построить график.
4. Какие размеры должен иметь цилиндр, площадь полной поверхности которого 96π см2, чтобы его объем был наибольшим?
5. Вычислить интегралы:
а)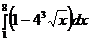 
б)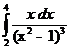 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = х2– 3х – 4 и Ох
7. Решить дифференциальное уравнение: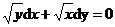
Вариант 4
1. Из двухсот рабочих норму выработки не выполняют 15 человек. Найти вероятность того, что:
а) два случайно выбранных рабочих не выполняют
норму;
б) из двух случайным образом выбранных рабочих
один выполняет норму, а второй нет.
2. Вычислить предел: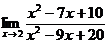 
3. Найти производную функции: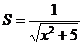 
и вычислить S' (2)
1. Исследовать функцию: у=х3–10,5х2+36х+1 и построить график.
2. Докажите, что из всех прямоугольников, имеющих периметр 36см, наибольшую площадь имеет квадрат.
3. Вычислить интегралы:
а)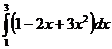 
б)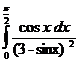 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной данными линиями: у2 = 4х и х2 = 4у
7. Решить дифференциальное уравнение: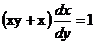 
Вариант 5
1. В читальном зале 6 учебников по теории вероятностей, из которых 3 в мягком переплете. Библиотекарь взял два учебника. Найти вероятность, что: а) оба учебника окажутся в мягком переплете;
б) один учебник в мягком переплете, а один - в твердом.
2. Найти производную функции: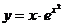 
и вычислить у'(0)
3. Исследовать функцию: у=х3–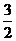 
х2 – 6х+1 и построить график
4. Какой из цилиндров с объемом 128 см3 имеет наименьшую полную поверхность?
5. Вычислить интегралы:
а)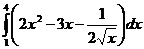 
б)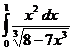 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями у = 5х – х2 + 6 и осью Ох
7. Решить дифференциальное уравнение: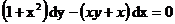 
Вариант 6
1. В партии из 10 деталей 7 стандартных. Найдите вероятность того, что среди 6 взятых наудачу деталей 4 будут стандартными.
2. Найти производную функции: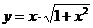 
и вычислить у' 
4. Исследовать функцию: у = х3–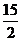 
х2+18х и построить график
5. Требуется приготовить ящик с крышкой, объем которого равен 288 см3, а стороны основания относятся как 1:3. Каковы должны быть размеры ящика, чтобы его полная поверхность была наименьшей?
6. Вычислить интегралы:
а)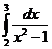 
б)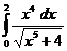 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = х3, у = х2, х = –1, х = 0
7. Решить дифференциальное уравнение: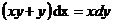 
Вариант 7
1. Жюри конкурса 10 претендентов одинаково достойных первой премии. Среди них оказались 5 научных сотрудников. 2 студента, 3 рабочих. Какова вероятность того, что в результате жеребьевки премия будет отдана либо ученому, либо студенту?
2. Найти производную функции f(x)= x · lnx – x и вычислить f '(e3)
3. Исследовать функцию: у = х3–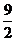 
х2 +6х и построить график
4. Около стены нужно сделать забор, чтобы огородить прямоугольный участок земли наибольшей площади. Общая длина забора 60 м. Найдите длину части забора, параллельной стене.
5. Вычислить интегралы:
а)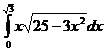 
б)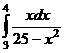 
6. Сделать чертеж и вычислить площадь фигуры, ограниченной линиями: у=х2– 6х+8 и осью Ох
7. Решить дифференциальное уравнение: х2у /– 2ху=3у
Вариант 8
1. Из 15 билетов выигрышными являются 4. Какова вероятность того, что среди зятых наудачу 6 билетов будут 2 выигрышных?
2. Найти производную функции: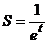 
и вычислить S' (0)
3. Исследовать функцию: у=х3 –х и построить график.
4. Гипотенуза прямоугольного треугольника равна 8 см. Найдите длину каждого катета, если площадь треугольника должна быть наибольшей.
5. Вычислить интегралы:
а)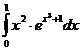 
б)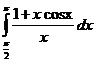 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = х2 и у = х + 2
7. Решить дифференциальное уравнение и найти частное решение: x2dx+ydy=0, если у=1 при х=0
Вариант 9
1. Для доступа в компьютерную сеть оператору необходимо набрать пароль из 4 цифр. Оператор забыл или не знает необходимого кода. Сколько всевозможных комбинаций он может составить для набора пароля, если а) цифры в коде не повторяются; б) повторяются.
2. Найти производную функции: y=tg2x – ctg2x и вычислить y'
3. Исследовать функцию: у=6х3– x2 и построить график
4. Докажите, что из всех прямоугольников с площадью 400 см2 квадрат имеет наименьший периметр.
5. Вычислить интегралы:
а)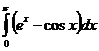 
б)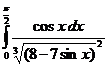 
6.Сделать чертёж и вычислить площадь фигуры, заключенной между линиями: у=х2 – 4х – 5 и осью Ох
7.Решить дифференциальное уравнение: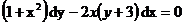 
,если у= –1 при х=0
Вариант 10
1. Монета подбрасывается 3 раза. Найти вероятность того, что при этом (безразлично в каком порядке) выпадет 2 раза герб и один раз цифра.
2. Найти производную функции: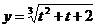 
и вычислить y' (2)
3. Исследовать функцию: у=х3– 4х2– 3x+6 и построить график
4. Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 600 см2, найдите параллелепипед наибольшего объема и определите его размеры.
5. Вычислить интегралы:
а)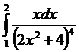 
б)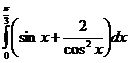 
6. Сделать чертёж и вычислить площадь фигуры, заключенной между линиями: у=6х – 3х2 и осью Ох
7. Решить дифференциальное уравнение:
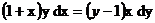,если у=1 при х=1
Вариант 11
1. Группа туристов из12 юношей и 7 девушек выбирают по жребию 5 человек для приготовления ужина. Сколько существует способов, при которых в эту группу пятерку попадут: 1 юноша и 4 девушки?
2. Найти производную функции: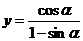 
и вычислить y'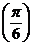 
3. Исследовать функцию: у = х4 – 8x2 – 9 и построить график
4. Каковы должны быть размеры цилиндрического сосуда емкостью 8π литров открытого сверху, чтобы на его изготовление потребовалось наименьшее количество материала?
5. Вычислить интегралы:
а)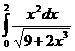 
б)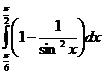 
6. Сделать чертеж и вычислить площадь фигуры, заключённой между линиями: у = х2 + 2 и у = 2х + 2
7. Решить дифференциальное уравнение:
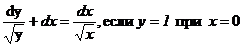
Вариант 12
1. Десять различных книг расставляются наудачу на одной полке. Найти вероятность того, что три определенные книги окажутся поставленными рядом.
2. Найти вторую производную функции: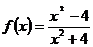 
и вычислить f '' (–1)
3. Исследовать функцию: у = х3– 2x 2+ x и построить график
4. Путь S в метрах, пройденным телом за t секунд при прямолинейном движении, определяется управлением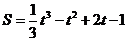 
. Найти скорость и ускорение в конце третьей секунды.
5. Вычислить интегралы:
а)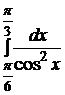 
б) 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = х2 + 1, у = 0, х = 2, х = 5
7. Решить дифференциальное уравнение:
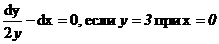
Вариант 13
1. Бросают одновременно две игральные кости. Найти вероятность следующих событий:
А – « сумма выпавших очков равна 8»;
В – «произведение выпавших очков равно 8»;
С – «сумма выпавших очков больше, чем их произведение ».
2. Найти производную функции: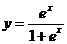 
и вычислить y'(0)
3. Исследовать функцию: у=2х3–3x2 и построить график
4. Найдите наибольшее и наименьшее значения функции: у = х5 – 5х4 + 5х3+1 на отрезке [–1;2]
5. Вычислить интегралы:
а)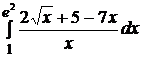 
б)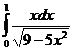 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = 2х – х2 и у = х
7. Решить дифференциальное уравнение:
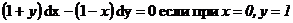
Вариант 14
1. В классе 17 девочек и 14 мальчиков. Определите вероятность того, что оба вызванных ученика окажутся: а) мальчиками; б) девочками, в) один мальчик и одна девочка.
2. Найти производную функции: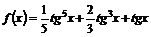 
и вычислить
f '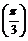 
3. Исследовать функцию: у = х3 – 3x2 и построить график
4. Число 50 представьте в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было наибольшим.
5. Вычислить интегралы:
а)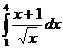 
б)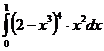 
6. Сделать чертеж и вычислить площадь фигуры, заключенной между линиями: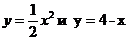 
7. Решить дифференциальное уравнение: 2у'=у, если при х=0 у=1
Вариант 15
1. Владимир хочет пригласить к себе в гости троих из семи своих лучших друзей. Сколькими способами он может это сделать? (35)
2. Найти производную функции: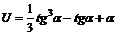 
и вычислить U' 
3. Исследовать функцию: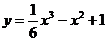 
и построить график
4. Найти наибольшее и наименьшее значения функции: у = х4 – 2 х2+5 на отрезке: –2 ≤ х ≤ 2
5. Вычислить интегралы:
а)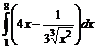 
б)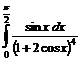 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: х2 – 9у = 0 и х – 3у + 6 = 0
7. Решить дифференциальное уравнение: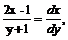
если при х=5 у=0
Вариант 16
1.Какова вероятность того, что наудачу выбранное целое число от 40 до 70 является кратным 6?
2.Найти производную функции: у =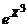 
и вычислить у"(0)
3.Исследовать функцию: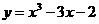 
и построить график
4.Напишите уравнение касательной к кривой: у=х3+2х2–3х в точках её пересечения с осью Ох
5.Вычислить интегралы:
а)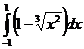 
б)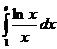 
6.Сделать чертёж и вычислить площадь фигуры, заключенной между линиями: 4у – х3 =0; у – х = 0
7.Решить дифференциальное уравнение:
Вариант 17
1.На втором курсе изучаются 14 предметов. Сколькими способами можно составить расписание занятий на пятницу, если в этот день недели должно быть четыре различных предмета?
2.Найти вторую производную функции: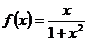 
и вычислить f"(2)
3.Исследовать функцию: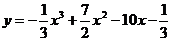 
и построить график.
4. Найти наибольшее и наименьшее значения функции: у = х3 – 3х2 + 3x + 2 на отрезке: – 2 ≤ х ≤ 2
5.Вычислить интегралы:
а)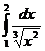 
б)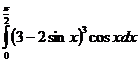 
6.Сделать чертёж и вычислить площадь фигуры, заключенной между следующими кривыми: у2 = х и у = х2
7.Решить дифференциальное уравнение:
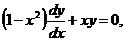если у = 4 при х = 0
Вариант 18
1. Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, что среди трех наугад выбранных вопросов студент
знает: а) 3 вопроса; б) 1 вопрос.
2. Найти производную функции: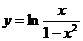 
и вычислить у' (2)
3. Исследовать функцию: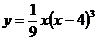 
и построить график
4. Какое положительное число, будучи сложено с обратным ему числом, дает наименьшую сумму.
5. Вычислить интегралы:
а)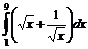 
б)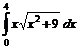 
6. Сделать чертёж и вычислить площадь фигуры, заключенной между кривыми: у = х2 и у = 1 – х2
7. Решить дифференциальное уравнение:
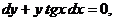если х = 0 при у = 1
Вариант 19
1. При игре в нарды бросают 2 игральных кубика. Какова вероятность того, что на обоих кубиках выпадут одинаковые числа?
2. Найти вторую производную функции: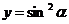 
и вычислить f"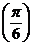
3. Исследовать функцию: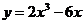 
и построить график
4. Из квадратного листа жести со стороной а требуется сделать открытый сверху ящик наибольшего объема, имеющий квадратное основание.
5. Вычислить интегралы:
а)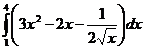 
б)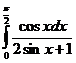 
6. Сделать чертёж и вычислить площадь фигуры, заключенной между следующими кривыми: 4х2–9у + 18 = 0 и 2х2– 9у + 36=0
7. Решить дифференциальное уравнение:
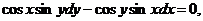если у = π при х = π
Вариант 20
1. В ящике лежат 1 белый и три черных шара. Наугад вынимаются 2 шара. Какова вероятность того, что вынуты: 1) 2 черных шара; 2) белый и черный шар?
2. Найти производную функции: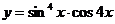 
и вычислить у' (0)
3. Исследовать функцию: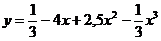 
и построить график
4. Прямоугольный участок земли в 10000 м2 нужно окопать вдоль всей границы рвом. Как выбрать размеры участка, чтобы длина рва была наименьшая.
5. Вычислить интегралы:
а)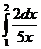 
б)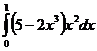 
6. Сделать чертёж и вычислить площадь фигуры, заключенной между линиями: у = х2 – 8х + 16 и х + у – 6 = 0
7. Решить дифференциальное уравнение: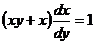 
Вариант 21
1.Набирая номер телефона, состоящий из 7 цифр, абонент забыл, в какой последовательности идут три последние цифры. Помня лишь, что это цифры 1, 5 и 9, он набрал первые четыре цифры, которые знал, и наугад комбинацию из цифр !, 5 и 9. Какова вероятность того, что абонент набрал правильный номер?
2.Найти производную функции: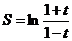 
и вычислить S' (3)
3.Исследовать функцию: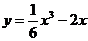 
и построить график
4.Сумма основания и высоты треугольника равна 10 см. Каковы должны быть размеры основания и высоты, чтобы площадь треугольника была наибольшая.
5.Вычислить интегралы:
а)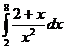 
б)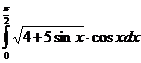 
6.Сделать чертёж и вычислить площадь фигуры, заключенной между линиями: у = 3х – 1, у = 0, х = 2, х = 4
7.Решить дифференциальное уравнение:
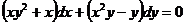
Вариант 22
1. На каждой карточке написана одна из букв О, П, Р, С, Т. Несколько карточек наугад выкладывают одну за другой в ряд. Какова вероятность, что при выкладывании:
а) 3-х карточек получится слово РОТ;
б) 4-х карточек получится слово СОРТ;
2. Найти производную функции: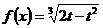 
и вычислить f '(4)
3. Исследовать функцию: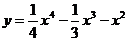 
и построить график
4. Из квадратного листа железа, сторона которого равна 30см, нужно вырезать по углам четыре квадрата так, чтобы из оставшейся части после сгибания получить коробку наибольшей емкости. Каковы при этом размеры вырезанных квадратиков?
5. Вычислить интегралы:
а)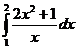 
б)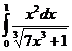 
6. Сделать чертёж и вычислить площадь фигуры, заключенной между линиями х – 2у + 4 = 0 и х + у – 5 = 0; у = 0
7. Решить дифференциальное уравнение: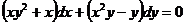
Вариант 23
1. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
2. Найти производную функции: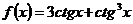 
и вычислить f ' 
3. Исследовать функцию: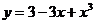 
и построить график
4. Из листа картона прямоугольной формы размером 30х50 см2 нужно вырезать по углам квадратики так, чтобы из оставшейся части после сгибания получить коробку наибольшей боковой поверхности. Подсчитать размеры вырезанных квадратиков.
5. Вычислить интегралы:
а) 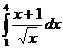б)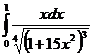 
6. Сделать чертёж и вычислить площадь фигуры, заключенной между линиями: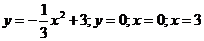 
7. Решить дифференциальное уравнение: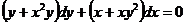 
Вариант 24
1. Четыре билета на елку распределили по жребию между 15 мальчиками и 12 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 2 девочкам.
2. Найти производную функции: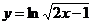 
3. Исследовать функцию: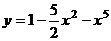 
и построить график
4. Окно имеет форму прямоугольника, который сверху заканчивается правильным треугольником. Периметр окна равен 3см. Каково должно быть основание прямоугольника, чтобы окно имело наибольшую площадь?
5. Вычислить интегралы:
а) 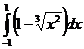б)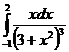 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = 9 – х2 , у = 0
7. Решить дифференциальное уравнение:
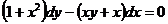
Вариант 25
1. Группа шахматистов сыграла между собой 28 партий. Каждые два из них встречались между собой один раз. Сколько шахматистов участвовало в соревновании?
2. Найти производную функции: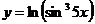 
3. Исследовать функцию: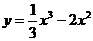 
и построить график
4. Сечение шлюзового канала имеет вид прямоугольника заканчивающегося полукругом. Периметр сечения равен 4,5м. При каком радиусе полукруга сечение будет иметь наибольшую площадь?
5. Вычислить интегралы:
а)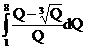 
б)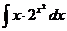 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = х2 – 2х + 3, у = 0, х = 0, х = 3
7. Решить дифференциальное уравнение: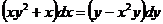 
Вариант 26
1. Сколько экзаменационных комиссий состоящих из семи человек можно образовать из четырнадцати преподавателей?
2. Найти производную функции: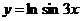 
3. Исследовать функцию: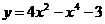 
и построить график
4. Требуется изготовить ящик с крышкой, объём которого равен 72 дм3, а стороны основания относятся , как 1:2. каковы должны быть размеры всех сторон его, чтобы полная поверхность ящика была наименьшей?
5. Вычислить интегралы:
а)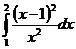 
б)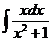 
6. Сделать чертёж и вычислить площадь фигуры, заключенной между линиями у = 4х – х2; у = 0
7. Решить дифференциальное уравнение: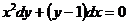 
Вариант 27
1. В библиотеке 10 книг по информационным технологиям, которые рекомендуется прочитать во время каникул. Сколькими способами студент может выбрать из них 3 книги?
2. Найти производную функции: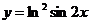 
3. Исследовать функцию: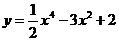 
и построить график
4. Объём правильной четырехугольной призмы равен 8 дм3. Какова должна быть сторона основания призмы, чтобы полная поверхность ее была наименьшей?
5. Вычислить интегралы:
а)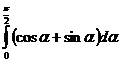 
б)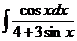 
6. Сделать чертёж и вычислить площадь фигуры ограниченной линиями: у = х2; х = у2
7. Решить дифференциальное уравнение: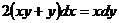 
Вариант 28
1. Сколькими способами можно расставить 9 различных книг на полке, чтобы определенные 4 книги стояли рядом?
2. Найти производную функции: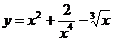 
3. Исследовать функцию: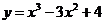 
и построить график
4. Резервуар ёмкостью в 4 м3 с квадратным основанием, открытый сверху, нужно выложить оловом. Каковы должны быть размеры резервуара, чтобы израсходовать для этого минимальное количество олова?
5. Вычислить интегралы:
а)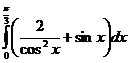 
б)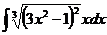 
6. Вычислить площадь фигуры, ограниченной линиями: у = х2, 5х – у – 6 = 0
7. Решить дифференциальное уравнение:
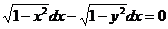
Вариант 29
1. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных.
2. Найти производную функции: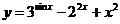 
3. Исследовать функцию: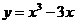 
и построить график
4. Найти величину радиуса основания и высоту цилиндра, имеющего объем 27π см3, у которого полная поверхность наименьшая.
5. Вычислить интегралы:
а)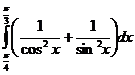 
б)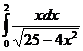 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: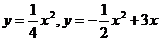 
7. Решить дифференциальное уравнение: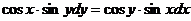 
Вариант 30
1. Из 200 рабочих норму выработки не выполняютю15 человек. Найти вероятность того, что 2 случайно выбранных человека не выполняют нармы.
2. Найти производную функции: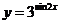 
3. Исследовать функцию: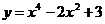 
и построить график
4. Какими нужно взять размеры цилиндрического сосуда ёмкостью в 1 л., открытого сверху, чтобы на его изготовление потребовалось наименьшее количество материала.
5. Вычислить интегралы:
а)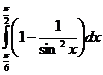 
б)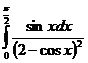 
6. Сделать чертёж и вычислить площадь фигуры, ограниченной линиями: у = – х 2 + 6; у = 2х + 3
7. Решить дифференциальное уравнение: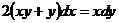 
МАТЕМАТИКА
Контрольные задания для студентов-заочников
Специальностей
«Экономика и бухгалтерский учёт»
Г. Алатырь, 2010 г.
| РАССМОТРЕНО предметной комиссией гуманитарных и естественнонаучных дисциплин Протокол № _____ от «____»_______ 2010 г. Председатель _________________________ |