Тема 3 Дифференциальные уравнения

Задача 1. Решить уравнение у' — y tgx= — у²cos х.

Решение. Данное уравнение является уравнением Бернулли. Для его решения (как и для решения линейного уравнения) искомую функцию у представим в виде произведения двух других функций: и=и(х) и v=v'(х), то есть введем подстановку у=и v. Тогда у'=и'v+v'и, и данное уравнение примет вид:

и'v+иv' - uv tg х= - и'v' cos x

или

v (и' - и tg х) +иv'= - u² v² cos x (1)

Выберем функцию и так, чтобы

(и' - и tg х) =0 (2)

При подобном выборе функции u уравнение (1) примет вид

иv'=-u²v² cos x или v'= — uv²cos x (3)

Решая (2) как уравнение с разделяющимися переменными, имеем:

, , .

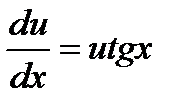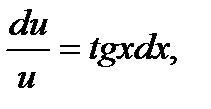
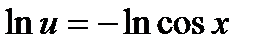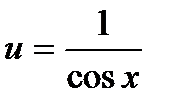Здесь произвольная постоянная С=0. Подставляя найденное значение и в уравнение (3) имеем:

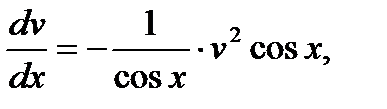
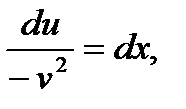
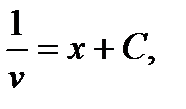
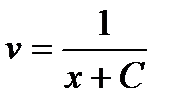
Тогда у=иv= 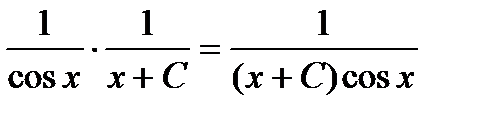- общее решение данного уравнения.

Задача 2. Найти частное решение уравнения у"+4у=4sin2x—8соs2х, удовлетворяющее начальным условиям у(0)=0, у'(0) =0.

Общее решение у данного уравнения равно сумме общего решения у_одн однородного уравнения и какого-либо частного решения у данного уравнения, то есть y=y_одн+ .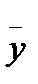

Для нахождения у_одн составим х а р а к т е р и с т и ч е с к о е уравнение k²+4=0, имеющее комплексные корни k_i=2i и k₂=-2i. В этом случае общее решение одно­родного уравнеия ищем в виде y_одн=e^ax(C₁ cos 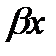+C₂ sin 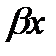) , где 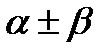i – комплексные корни характеристического уравнеия. Подставим в (4) 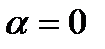, , 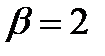имеем: y_одн= C₁ cos2x+C₂ sin2x

Для нахождения частного решения 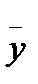неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция f(x)=e^ax(a cos 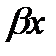+b sin 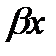) и числа 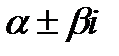не являются корнями характеристического уравнения, то существует частное решение 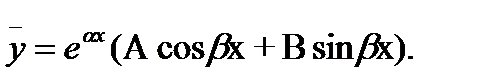. Если же числа 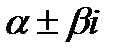являются корнями характеристического уравнения, то существует частное решение

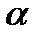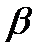Применяя эту теорему при =0, =2, имеем: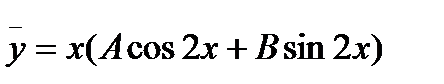

Дважды дифференцируя последнее равенство, находим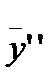

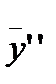=(4B — 4Ах)cos2х+(—4А — 4Вх) sin 2х.

Подставив в данное уравнение у и 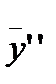, получим:

4В cos 2х — 4А sin 2х=4 sin 2х — 8 cos 2х, откуда А= — 1, В= — 2.

Значит, 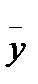= — x(соs 2х+2 sin2х) и у= С₁соs 2х+С₂ sin 2 - x(соs 2х+2 sin 2x)

Найдем у'. у'=-2С₁ sin 2х+2С₂соs 2х- соs 2х-2sin 2х- х(-2 sin2х+4 соs 2х).

Используя начальные условия, получим систему:

С₁=0

2С₂ – 1=0, откуда С₁=0, С₂= .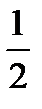

Следовательно, у= 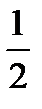sin 2х — x(соs 2х+2 sin 2х) есть искомое частное решение данного дифференциального уравнения.

Вопросы для самопроверки

1.Что навязывается дифференциальным уравнением?

2.Что называется общим решением дифференциального уравнения? частным решением?

3.Каков геометрический смысл частного решения дифференциального. уравнения первого порядка?

4.Приведите примеры дифференциальных уравнений с разделяющимися переменными.

5. Какое дифференциальное уравнение первого порядка называется линейным? уравнением Бернулли? Укажите способ их решения.

6.Какое уравнение называется линейным дифференциальным уравнением второго порядка?

7.Какое уравнение называется характеристическим для однородного ддифференциального уравнения второго порядка?

8. Какой вид имеет общее решение однородного дифференциального уравнения второго порядка в зависимости от дискриминанта характеристического уравнения?

9. Как найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?

10. Какой вид имеет частное решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его правая часть есть многочлен? показательная функция? тригонометрическая функция?

Тема 4 Ряды

Задача 1. Написать первые три члена ряда 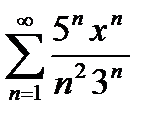найти интервал сходимости ряда и исследовать его сходимость на концах интервала.

Решение: Беря последовательно n=1, 2, 3, ..., запишем данный ряд в виде:

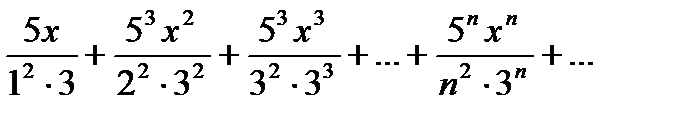
Для нахождения области сходимости ряда применим признак Даламбера

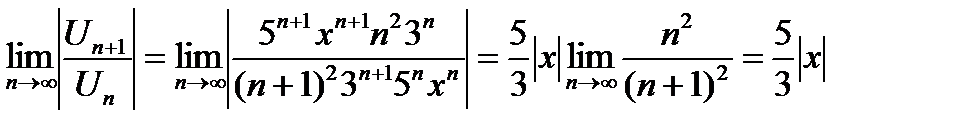
Данный ряд сходится абсолютно при тех значениях х, которые удовлетворяют неравенству 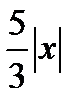<1, или |x|< 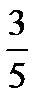, или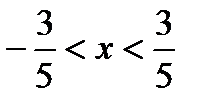

Исследуем сходимость ряда на концах полученного интервала. При х= 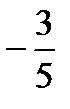данный ряд принимает вид .

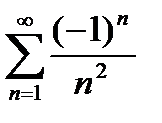Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при 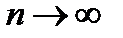. Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит, х — принадлежит области сходимости данного ряда.

При х= 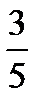данный ряд принимает вид 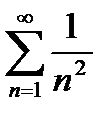. Исследуем сходимость этого ряда при помощи интегрального пpизнака сходимости Коши. Рассмотрим несобственный интеграл

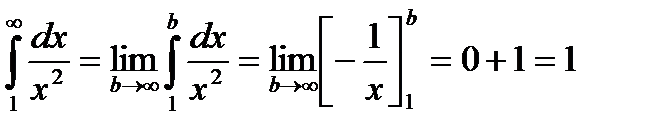
Так, как несобственный интеграл сходится, то сходится и исследуемый ряд. 3начит, при х= 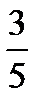исходный ряд сходится. Таким образом, 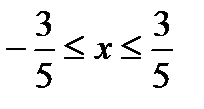область сходимости данного ряда.

Задача 2.Вычислить 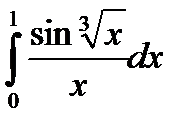с точностью до 0,001.

Представим подынтегральную функцию в виде степенного ряда. Заменив х в разложении функции sin х на 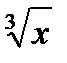, имеем:

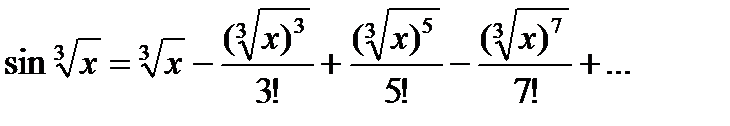
Тогда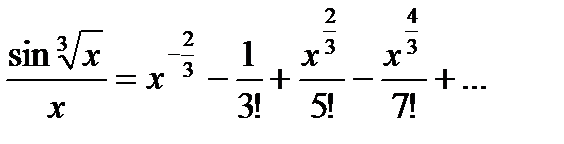

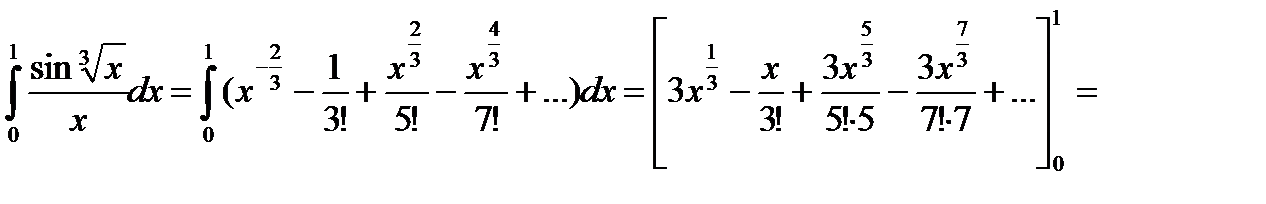
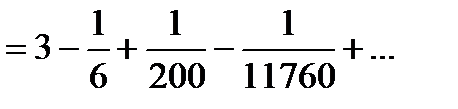
Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвертый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда

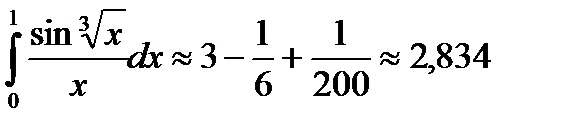
Вопросы для самопроверки

1. Что называется числовым рядом?

2. Что называется n-й частичной суммой числового ряда?

3. Какой числовой ряд называется сходящимся?

4. Что является необходимым условием сходимости числового ряда?

5. Назовите достаточные признаки сходимости, основанные на сравнении рядов.

6. Назовите признак Даламбера сходимости рядов, радикальный признак сходимости Коши?

7. В чем состоит интегральный признак сходимости Коши?

8. Какие ряды называются знакочередующимися? Приведите примеры.

9. Сформулируйте признак Лейбница сходимости знакочередующихся рядов.

10. Какие знакочередующиеся ряды называются абсолютно сходящимися? условно сходящимися?

11. Дайте определение степенного ряда и области его сходимости.

12. Kaк найти область сходимости степенного ряда?

13. Запишите разложение в степенной ряд функций е^x, sin х, соs х, (1+x)^m, 1n 5(1+х).

14. Как обеспечивается требуемая точность при применении степенны рядов в при­ближенных вычислениях?