Тема 1 Элементы линейной алгебры
Уфа 2010
УДК 51
ББК 22.14
М 54
Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства (протокол № 2 от 24 февраля 2010 года)
Составитель: доцент Костенко Н.А.
Рецензент: доцент кафедры бухгалтерского учета и аудита Насырова А.Д.
Ответственный за выпуск: зав каф. математики доцент Лукманов Р.Л.
Оглавление
| Введение | |
| Общие методические указания | |
| Тема 1 Элементы линейной алгебры | |
| Тема 2 Аналитическая геометрия на плоскости | |
| Тема 3 Векторная алгебра и аналитическая геометрия в пространстве | |
| Тема 4 Введение в анализ | |
| Тема 5 Производная и дифференциал | |
| Тема 6 Приложения производной Тема 7 Функции нескольких переменных | |
| Задания для контрольной работы №1 | |
| Литература | |
Введение
Настоящие методические указания предназначены для студентов-заочников экономических специальностей Башкирского государственного аграрного университета.
Методические указания содержат общие рекомендация по изучению дисциплины, краткие указания к выполнению контрольных работ, образцы решения некоторых задач, контрольные задания.
Дисциплина " Математика" - одна из учебных дисциплин, составляющих основу высшего образования. Знание математики, умение применять ее методы к решению практических задач - необходимые условия подготовки специалистов в высших учебных заведениях.
Задачи изучения курса математики вытекают из требований ГОСа и квалификационной характеристики выпускника, который должен уметь:
- строить простейшие математические модели экономических задач;
- выбрать нужный метод для решения этих задач и решать эти задачи;
-уметь выработать на основе полученных решений практические рекомендации.
Целью данных методических указаний являются оказание теоретической и практической помощи студентам – заочникам в выполнении контрольной работы №1, в усвоении теоретического материала дисциплины и в подготовке к сдаче итогового испытания.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях.
Номер варианта по каждому заданию студент выбирает по формуле Ni=ab+c,
где Ni – номер варианта,
a - номер задания,
b - предпоследняя цифра шифра студента,
c - последняя цифра шифра
Пример. Пусть шифр студента 1235, тогда:
Номер варианта первого задания: N1=1×3+5=8;
Номер варианта второго задания N2=2×3+5=11;
Номер варианта третьего задания N3=3×3+5=14;
Номер варианта четвертого задания N4=4×3+5=17.
Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
Если итоговая цифра по формуле получится число больше 20, то для определения варианта от полученной цифры отнимают 20.
Пример. Путь шифр студента 1298.
Номер варианта второго здания: N2=2×9+9=26. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
Общие методические указания
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом: чтение учебников, решение задач, выполнение контрольных заданий.
Если в процессе изучения материала или при решении задач у студента возникают трудности, то можно обратиться к. преподавателю кафедры математики для получения устной, или письменной консультации. В случае письменной консультации студент должен точно указать характер затруднения, полное название учебника или задачника, год издания и страницу, где находится непонятный для студента вопрос или задача.
При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тет-ради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, номер контрольной работы, дата ее отсылки в институт, домашний адрес студента.
2. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условие.
3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.
4. Решение, задач геометрического содержания должно сопровождаться чертежами (желательно на миллиметровой бумаге), выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах.
5. На каждой странице тетради, необходимо оставлять поля шириной 3 — 4 см для замечаний преподавателя.
6. Контрольные работы должны, выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена.
Изучите теорию по указанным разделам, разберите решения задач, приведенных в данных методических указаниях и приступайте к выполнению контрольных работ. Желаем удачи!
Рис.1
На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АВС, высота CD, окружность с центром в точке Е.
Задача 2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки A(3; 0) и до прямой х=12 равно числу 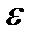 =0,5. Полученное уравнение привести к простейшему виду и построить кривую.
=0,5. Полученное уравнение привести к простейшему виду и построить кривую.
Решение. Пусть М(х; у) — текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр МВ на прямую х=12 (рис. 2). Тогда В (12; у).
По условию задачи 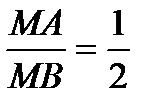 . По формуле (1) из предыдущей задачи
. По формуле (1) из предыдущей задачи
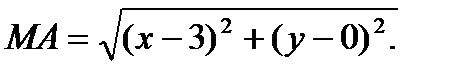
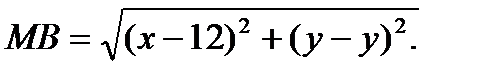
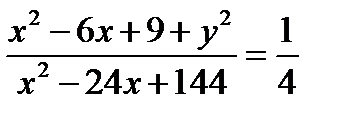 Тогда
Тогда 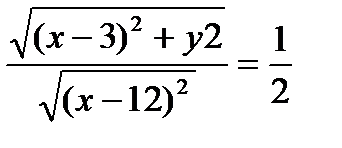 ,
,
4x2 – 24x+36+4y2 = x2– 24x +144, 3x2+4y2=108,
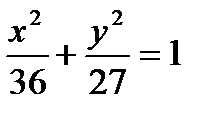 Полученное уравнение представляет собой эллипс вида
Полученное уравнение представляет собой эллипс вида 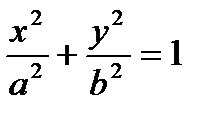 , где а = 6, b =
, где а = 6, b = 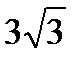 .
.
Определим фокусы эллипса F1( - с; 0) и F2 (c; 0). Для эллипса справедливо равенство b2 = a2 - c2 , откуда c2 = a2 - b2 = 9 и с = 3. То есть, F1 ( -3; 0) и F2 (3; 0) — фокусы эллипса (точки F и А совпадают). Эксцентриситет эллипса 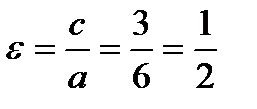
у
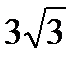
М В
F1 А
-3 0 3 6 12 x
Рис. 2
Задача 3. Составить ypaвнение линии, для каждой точки которой ее расстояние до точки А (3; — 4) равно расстоянию до прямой у=2. Полученное уравнение привести к простейшему виду и построить кривyю.
Решение. М(х;у) — текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую у = 2 (рис. 3). Тогда В (х; 2). Так как МА=МВ, то
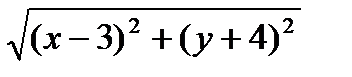
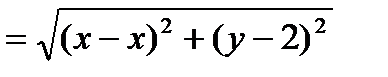 или
или
(x-3)2+y2+8y+16= y2-4y+4
-12y-12=(x-3) 2
y+1= 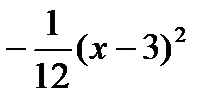
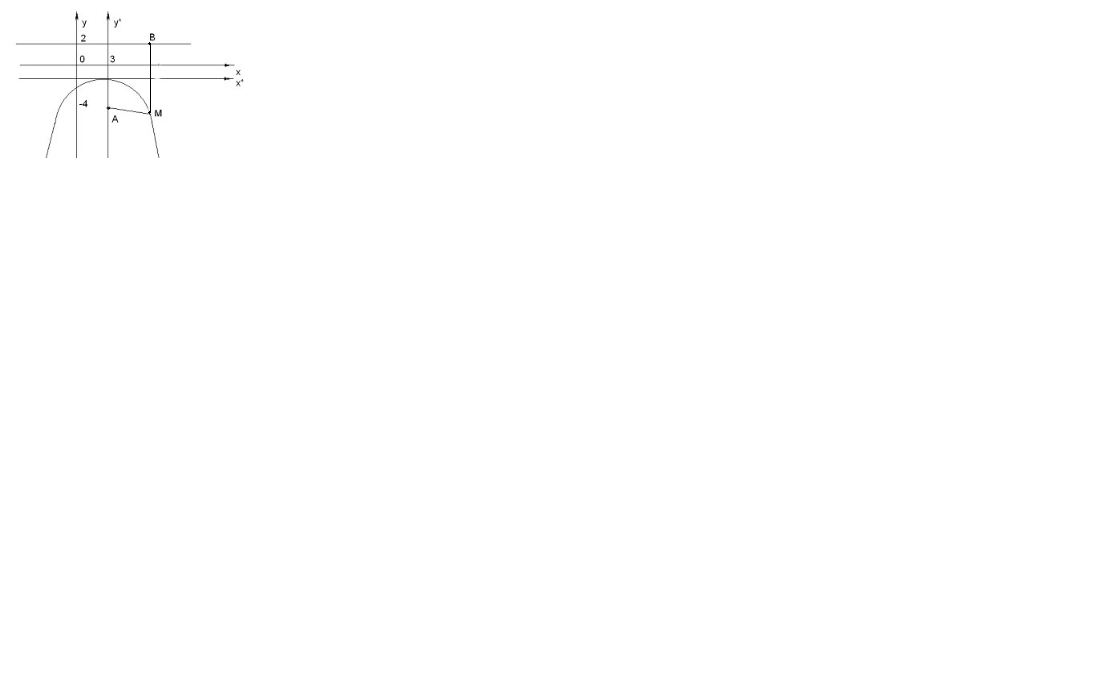
Рис.3
Полученное уравнение определяет параболу с вершиной в точке О*(3; — 1). Для приведения уравнения параболы к простейшему (каноническому) виду положим
x – 3 = X*, y+1=Y*. Тогда в системе координат Х*0*У* уравнение параболы принимает следующий вид: У*= 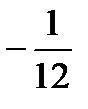 (Х*)2. В системе координат Х*0*У* строим параболу.
(Х*)2. В системе координат Х*0*У* строим параболу.
Вопросы для самопроверки
1. Дайте определение прямоугольной декартовой системы координат.
2. Напишите формулу для нахождения расстояния между двумя точками.
3. Напишите формулы для определения координат точки, делящей данный отрезок в данном отношении.
4. Напишите формулы преобразования координат: а) при параллельном переносе системы координат; б) при повороте системы координат.
5. Напишите уравнения прямой: а) с угловым коэффициентом; б) проходящей через давленую точку в данном, направлении; в)проходящей через две данные точки; г) в «отрезках».
6. Как найти координаты точек пересечения двух прямых?
7. Напишите формулу для определения угла между двумя прямыми.
8. Каковы условия параллельности и перпендикулярности двух прямых?
9. Сформулируйте определение окружности.
10. Напишите уравнение окружности с центром в любой точке плоскости хОу; с центром в начале координат.
11. Дайте определение эллипса. Напишите каноническое уравнение эллипса.
12. Что называется эксцентриситетом эллипса? Как из-меняется форма эллипса с изменением эксцентриситета от 0 до 1?
13. Дайте определение гиперболы. Напишите каноническое уравнение гиперболы.
14. Напишите формулу для определения эксцентриситета гиперболы.
15. Напишите уравнения для нахождения асимптот гиперболы.
16. Сформулируйте определение параболы. Напишите каноническое уравнение параболы, симметричной относительно оси Оу.
В пространстве
Задача 4. Даны координаты трех точек: A(3; 0; -5), В,(6; 2; 1),С(12; -12; 3).
Требуется: 1) записать векторы 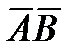 и
и 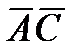 в системе орт и найти модули этих векторов; 2) найти угол между векторами
в системе орт и найти модули этих векторов; 2) найти угол между векторами 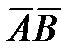 и
и 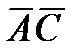 ; 3) составить уравнение плоскости, проходящей через точку С перепендикулярно вектору
; 3) составить уравнение плоскости, проходящей через точку С перепендикулярно вектору 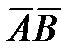 .
.
Решение. 1. Если даны точки М1(х1, у1, z1) и М2 (х2, у2, z2), то вектор 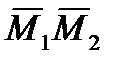 через орты
через орты 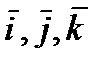 выражается следующим образом:
выражается следующим образом:
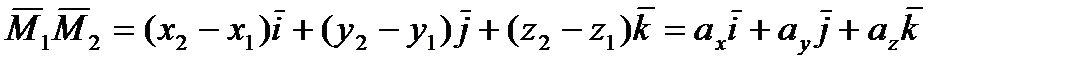 (1)
(1)
Подставляя в эту формулу координаты точек А и В, имеем:
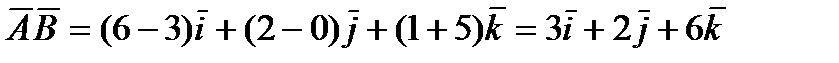
Подобным образом 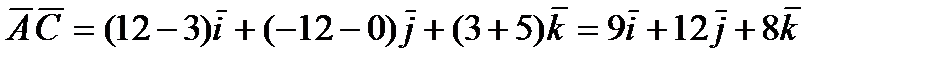
Модуль вектора 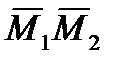 вычисляется по формуле:
вычисляется по формуле:
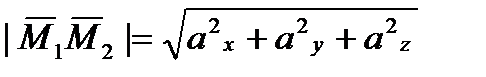 (2)
(2)
Подставляя в формулу (2) найденные ранее координаты векторов 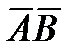 и
и 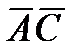 , находим их модули:
, находим их модули:
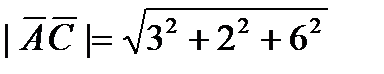
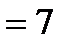
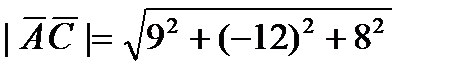 =17
=17
2. Косинус угла 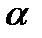 , образованного векторами
, образованного векторами 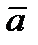 и
и 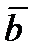 , равен их скалярному произведению, деленному на произведение их модулей:
, равен их скалярному произведению, деленному на произведение их модулей:
cos 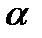 =
= 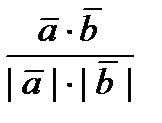 (3)
(3)
Так как скалярное произведение двух векторов, заданных своими координатами равно сумме попарныx произведений одноименных координат, то
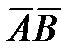 *
* 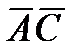 = 3*9+2*(-12)+6*8=51.
= 3*9+2*(-12)+6*8=51.
Применяя (3), имеем: сos 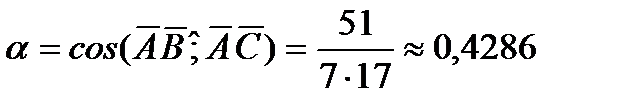
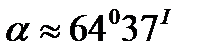
3. Известно, что уравнение плоскости, проходящей через точку М0(х0, у0, z0) перпендикулярно вектору 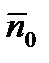 А; В; С имеет вид
А; В; С имеет вид
A(x – хо) +B(y – уо) + С(z – zо) =0 (4)
По условию задачи искомая плоскость проходит через точку С(12; - 12; 3) перпендикулярно вектору 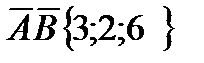
Подставляя в (4) А=3, В=2, С=6, хо = 12, уо = - 12, zо =3, получим:
3(х – 12)+2(у+12) +6(z – 3) = 0, Зх + 2у + 6z – 30=0 — искомое уравнение плоскости.
Вопросы для самопроверки
1. Какие величины называются скалярными, векторными?
2. Какие векторы навязываются коллинеарными?
3. Какие два вектора называются равными?
4. Как сложить два вектора? Как их вычесть?
5. Как найти координаты вектора по координатам точек его начала и конца?
6. Назовите правила сложения, вычитания векторов, заданных в координатной форме. Как умножить вектор на скаляр?
7. Дайте определение скалярного произведения двух векторов. Перечислите основные свойства скалярного произведения.
8. Как найти скалярное произведение двух векторов по их координатам?
9. Напишите формулу для определения угла между двумя векторами.
10.Напишите условия: коллинеарности двух векторов; их перпен-дикулярности.
11. Напишите общее уравнение плоскости.
12. Напишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
13.Какой вид имеет уравнение плоскости, проходящей через три данные точки?
14.Напишите формулу для определения расстояния от точки до плоскости.
Вопросы для самопроверки
1. Что называется определителем второго, третьего, n-го порядков?
2. Назовите основные свойства определителей.
3. Что называется минором, алгебраическим дополнением элемента определителя?
4. Напишите формулы Крамера решения системы линейных уравнений. В каких случаях их можно использовать?
5. Назовите схему решения системы линейных уравнений по методу Гаусса.
6. Что называется матрицей?
7. Как определяются основные действия над матрицами?
8. Какая матрица называется обратной по отношению к данной матрице? Как найти матрицу, обратную данной?
9. Что называется рангом матрицы? Как найти ранг матрицы?
10. Сформулируйте теорему Кронекера - Капелли.
11. Опишите матричный способ решения системы линейных уравнений.
12. Какова геометрическая интерпретация систем линейных уравнений и неравенств?
Тема 4 Введение в анализ
Разберите решение задач 6, 7 данного пособия.
Задача 6. Вычислить пределы:
a) 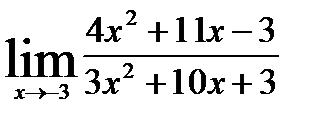 , б)
, б) 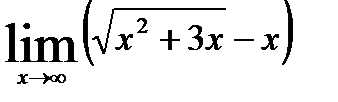
в). 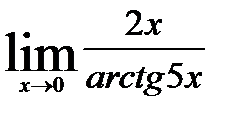 г)
г) 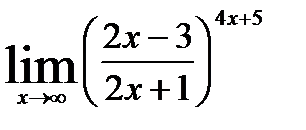
Решение. a) Подстановка предельного значения аргумента х= -3 приводит кнеопределенному выражению вида 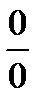 . Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при
. Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при 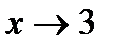 :
:
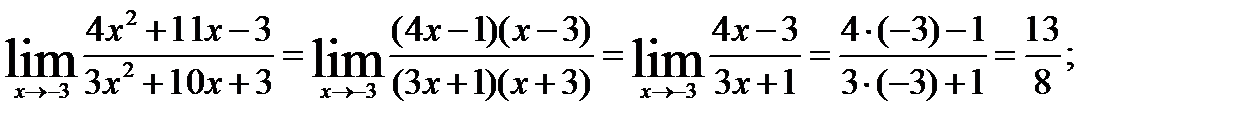
б). При 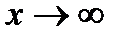 выражение
выражение 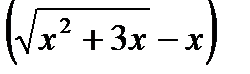 дает неопределенность вида
дает неопределенность вида 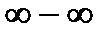 . Для ее устранения умножим и разделим это выражение на
. Для ее устранения умножим и разделим это выражение на 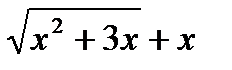
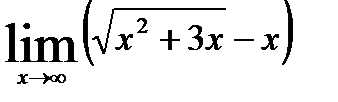 =
= 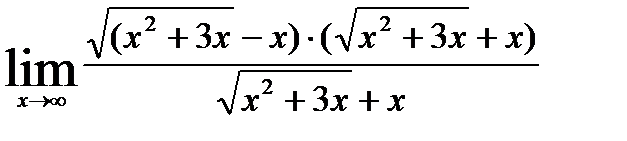 =
= 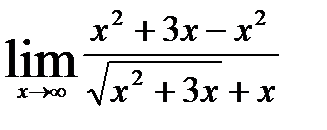 =
= 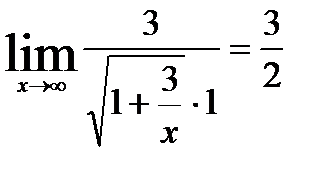 ;
;
в). Обозначим arctg5x=y. Тогда 5x=tg y и 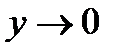 при
при 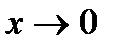 . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела 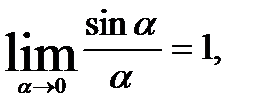 имеем:
имеем:
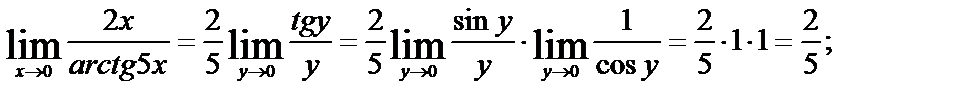
г). При 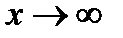 выражается
выражается 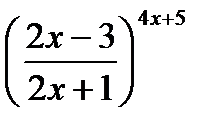 является неопределенностью вида
является неопределенностью вида 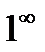 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при 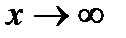 величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела: 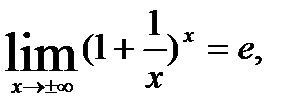
тогда имеем: 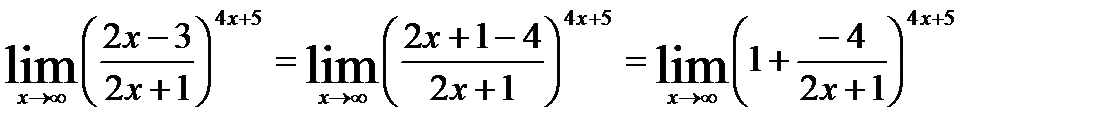
Пусть 2x+1=-4y. Тогда 4x+5=-8y+3 и 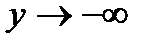 при
при 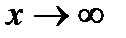 . Переходя к переменной y, получим:
. Переходя к переменной y, получим:
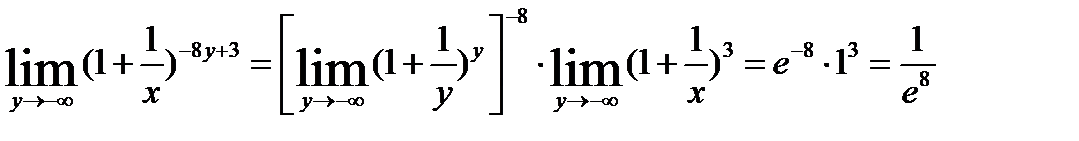
Задача 7. Исследовать на непрерывность функцию 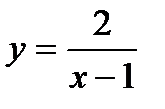 .
.
Решение. Данная функция является элементарной. Известно, что всякая элемен-тарная функция непрерывна на своей области определения. Данная функция определена на интервалах ( - 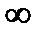 ; 1) и (1;
; 1) и (1; 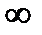 ) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 4.
) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 4.
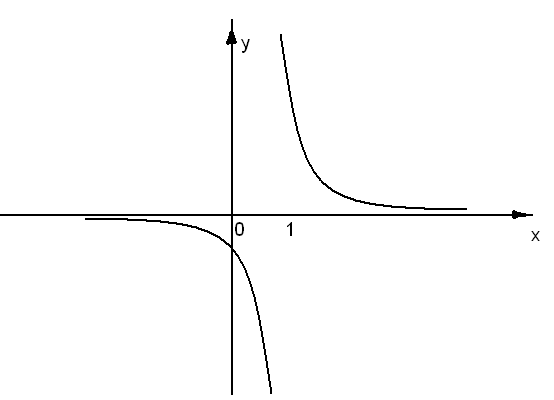
Рис. 4
Вопросы для самопроверки
1. Сформулируйте определение понятия функции.
2. Что называется областью определения функции? Областью изменения функции?
3. Перечислите основные элементарные функции. Назовите их основные свойства.
4. Какие функции называются элементарными? Приведите примеры.
5. Что называется пределом числовой последовательности?
6. Сформулируйте определение предела функции.
7. Назовите основные свойства пределов функций.
8. Какая функция называется бесконечно малой? Бесконечно большой?
9. Назовите свойства бесконечно малых функций.
10. Напишите формулы первого и второго замечательных пределов.
11. Какие логарифмы называются натуральными?
12. Дайте определение односторонних пределов функции в точке.
13. Какая функция называется непрерывной в точке? На интервале?
14. Какая точка называется точкой разрыва первого рода? Второго рода?
15. Перечислите основные свойства непрерывных на отрезке функций.
Задания для контрольной работы №1
Задание 1
В задачах 1-20 систему уравнений записать в матричной форме и решить ее помощью обратной матрицы.
1. 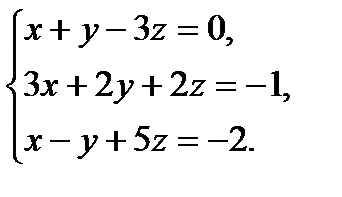 2.
2. 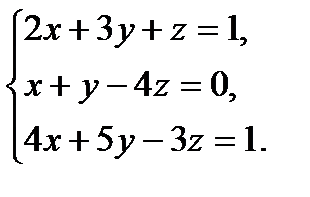
3. 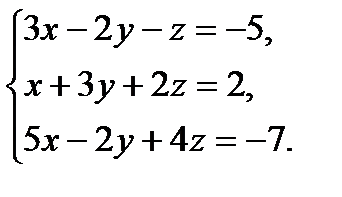 4.
4. 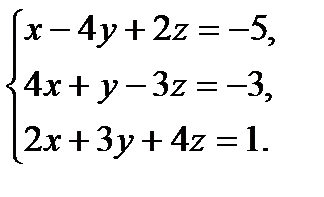
5. 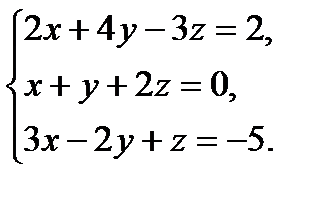 6.
6. 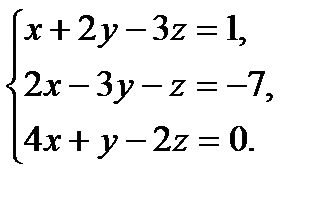
7. 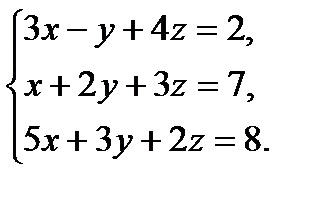 8.
8. 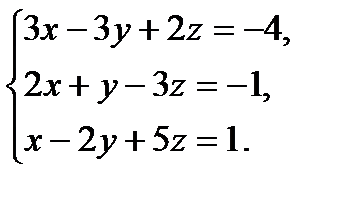
9. 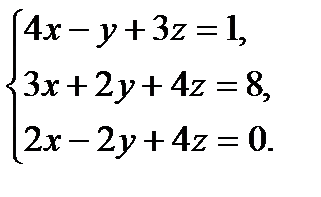 10.
10. 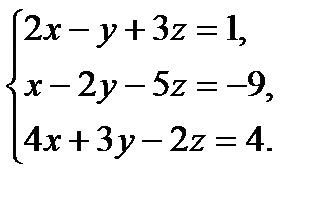
11. 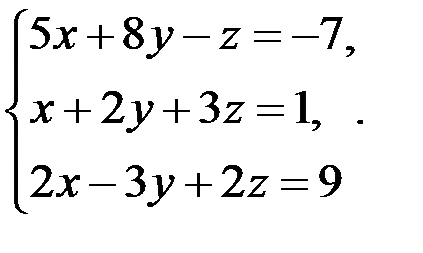 12.
12. 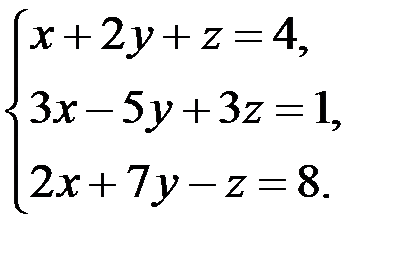
13. 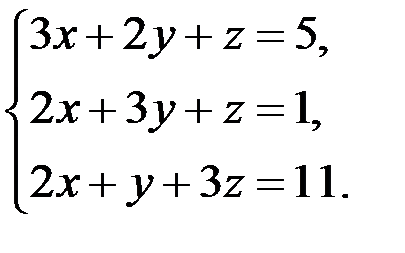 14.
14. 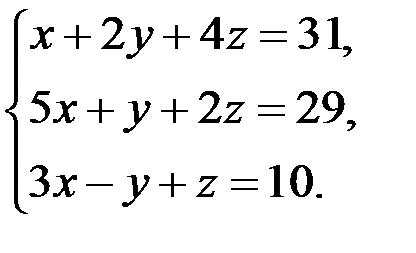
15. 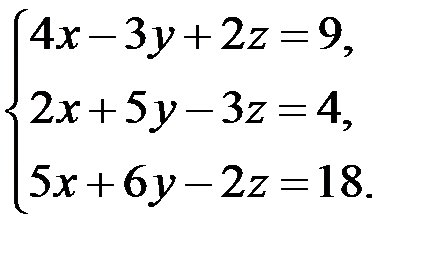 16.
16. 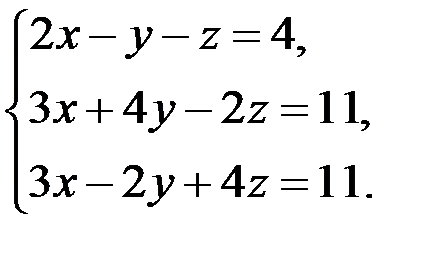
17. 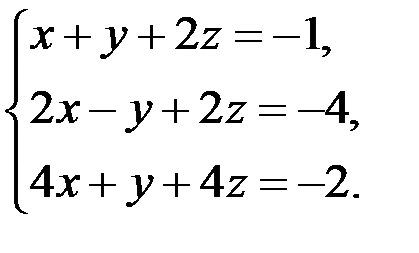 18.
18. 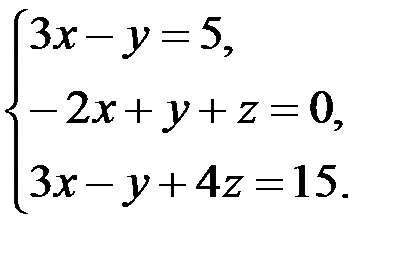
19. 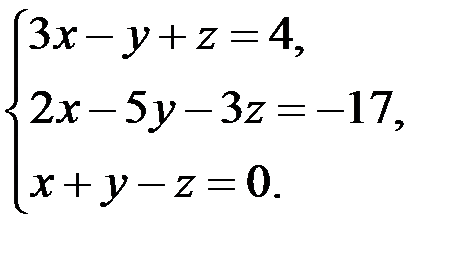 20.
20. 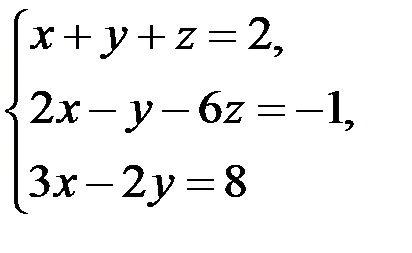
Задание 2
В задачах 1-20 даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А; 4) уравнения высоты СD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник ABC.
1. A (0;-1), B(12;8), C(10;-6). 2. A (-7; 2), B(5; 11), C(3; -3).
3. A (-5;-3), B(7;6), C(5;-8). 4. A (-6;-2), B(6;7), C(4;-7).
5. A (-3;3), B(9;-6), C(7;8). 6. А (-5; 0), B(7; 9), C(5; -5).
7. A (-6;11), B(6;10), C(4;-4). 8. A (-2;-4), B(10;5), C(8;-9).
9. A (-3;0), B(9;9), C(7;-5). 10. A (-9;2), B(3;7), C(1;-7).
11. A (-5;2), B(7;-7), C(5;7). 12. A (-7;5), B(5;-4), C(3;10).
13. A (-7;1), B(5;-8), C(3;6). 14. A (0;3), B(12;-6), C(10;8).
55. A (-8;4), B(4;-5), C(2;9). 16. A (-2;2), B(10;-7), C(8;7).
17. A (1;2), B(13;-7), C(11;7). 18. A (-4;1), B(8;-8), C(6;6).
19. A (-7;-1), B(-5;-10), C(3;4). 20. A (-8;-4), B(4;5), C(2;-9).
Задание 3
В задачах 1-10 составить уравнение линии, для каждой точки которой отношение расстояний до точки А (х1; у1) и до прямой х = а равно числу e. Полученное уравнение привести к простейшему виду и построить кривую.
1. A(4;0), a = 9, ε = 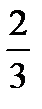 . 2. A(-8;0), a = - 2, ε =2.
. 2. A(-8;0), a = - 2, ε =2.
3. A(4;0), a = 1, ε = 2. 4. A(9;0), a = 4, ε = 1.5.
5. A(-1;0), a = -4, ε = 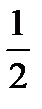 . 6. A(5;0), a =9, ε =
. 6. A(5;0), a =9, ε = 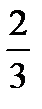 .
.
7. A(-1;0), a = -4, ε = 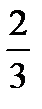 8. A(4;0), a = 7, ε =
8. A(4;0), a = 7, ε = 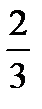
9. A(3;0),a = 8, ε = 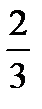 10. A(-4;0),a = -2, ε =3.
10. A(-4;0),a = -2, ε =3.
В задачах 11-20 составить уравнение линии, для каждой точки которой ее расстояние до точки А (х1; у1) равно расстоянию до прямой у = b. Полученное уравнение привести к простейшему виду и построить кривую.
11. А (2;1), b=- 1. 12. A (-2; -2), b= - 4.
13. A (2;-1), b=2. 14. A (2; -1), b=1.
15. A (4; -1), b=1. 16. А (4;1), b=- 1.
17. А (3;1), b=- 1. 18. А (2;1), b=- 2.
19. А (4;1), b=- 2. 20. А (6;1), b=- 1.
Задание 4
В задачах 1-20 даны координаты точек А, В, С. Требуется : 1) записать векторы 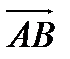 и
и 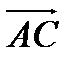 в системе орт и найти модули этих векторов; 2) найти угол между векторами
в системе орт и найти модули этих векторов; 2) найти угол между векторами 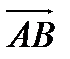 и
и 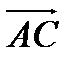 ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору
; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору 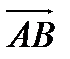 .
.
1. А(7;-4;1), B(12;-3;1), C(10;1;5). 2. А(0;-3;3), B(5;-2;3), C(3;2;7).
3. А(-2;-1;-2), B(3;0;-2), C(1;4;2). 4. А(-6;0;0), B(-1;1;0), C(-3;5;4).
5. А(-2;-3;-8), B(3;-2;-8), C(1;2;-4). 6. А(1;0;-1), B(6;1;-1), C(4;5;3).
7. А(-1;4;1), B(4;5;1), C(2;9;5).  8. А(3;-6;-3), B(8;-5;-3), C(6;-1;1).
8. А(3;-6;-3), B(8;-5;-3), C(6;-1;1).
9. А(1;0;0), B(6;1;0), C(4;5;4). 10.А(2;-8;-2),B(7;-7;-2), C(5;-3;2).
11. А(1;-2;3), B(0;-1;2),C(3;-4;5). 12.А(0;-3;6),B(-12;-3;-3),C(-9;-3;-6).
13. А(3;3;-1), B(5;5;-2), C(4;1;1) 14. А(-1;2;-3), B(3;4;-6), C(1;1;-1).
15. А(-4;-2;0), B(-1;-2;4), C(3;-2;1). 16. А(-3;-7;-5), B(0;-1;-2), C(2;3;0).
17. А(3;3;-1), B(1;5;-2), C(4;1;1). 18. А(0;0;4), B(-3;-6;1), C(-5;-10;-1).
19. А(7;0;2), B(7;1;3), C(8;-1;2). 20. А(0;3;-6), B(9;3;6), C(12;3;7).
Задание 5
Даны координаты вершин пирамиды АВСD. Найти:
1) векторы 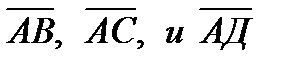 в системе орт и их модули;
в системе орт и их модули;
2) угол между векторами 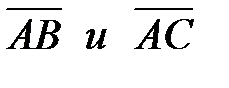 ;
;
3) площадь грани АВС;
4) объем пирамиды АВСD;
5) уравнение ребра АВ;
6) уравнение плоскости АВС;
7) уравнение и длину высоты, опущенной из точки D на плоскость АВС.
1. А(1;2;1), В(-1;5;1), С(-1;2;7), D(1;5;9).
2. А(2;3;2), В(0;6;2), С(0;3;8), D(2;6;10).
3. А(0;3;2), В(-2;6;2), С(-2;3;8), D(0;6;10).
4. А(2;1;2), В(0;4;2), С(0;1;8), D(2;4;10).
5. А(2;3;0), В(0;6;0), С(0;3;6), D(2;6;8).
6. А(2;2;1), В(0;5;1), С(0;2;7), D(2;5;9).
7. А(1;3;1), В(-1;6;1), С(-1;3;7), D(1;6;9).
8. А(1;2;2), В(-1;5;2), С(-1;2;8), D(1;5;10).
9. А(2;3;1), В(0;6;1), С(0;3;7), D(2;6;9).
10. А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10).
11. А(1;3;2), В(-1;6;2), С(-1;3;8), D(1;6;10).
12. А(0;1;2), В(-2;4;2), С(-2;1;8), D(0;4;10).
13. А(0;3;0), В(-2;6;0), С(-2;3;6), D(0;6;8).
14. А(2;1;0), В(0;4;0), С(0;1;6), D(2;4;8).
15. А(0;2;1), В(-2;5;1), С(-2;2;7), D(0;5;9).
16. А(1;1;1), В(-1;4;1), С(-1;1;7), D(1;4;9).
17. А(1;2;0), В(-1;5;0), С(-1;2;6), D(1;5;8).
18. А(0;1;0), В(-2;4;0), С(-2;1;6), D(0;4;8).
19. А(0;1;1), В(-2;4;1), С(-2;1;7), D(0;5;9).
20. А(0;2;0), В(-2;5;0), С(-2;2;6), D(0;5;8).
Задание 6
В задачах 1-20 даны векторы 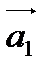 ,
, 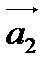 ,
, 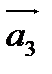 ,
,  . Показать, что векторы
. Показать, что векторы
 ,
,  ,
,  образуют базис трехмерного пространства и найти координаты вектора
образуют базис трехмерного пространства и найти координаты вектора  в этом базисе.
в этом базисе.
1.  (2;1;3),
(2;1;3),  (3;-2;1),
(3;-2;1),  (1;-3;-4),
(1;-3;-4),  (7;0;7).
(7;0;7).
2.  (5;3;1),
(5;3;1),  (-2;-1;2),
(-2;-1;2),  (-2;1;4),
(-2;1;4),  (3;0;1).
(3;0;1).
3.  (1;3;5),
(1;3;5),  (-2;-1;-1),
(-2;-1;-1),  (4;-2;4),
(4;-2;4),  (-7;3;-1).
(-7;3;-1).
4.  (3;1;6),
(3;1;6),  (-2;2;-3),
(-2;2;-3),  (-4;5;-1),
(-4;5;-1),  (3;0;1).
(3;0;1).
5.  (4;1;4),
(4;1;4),  (-2;-1;1),
(-2;-1;1),  (3;1;5),
(3;1;5),  (-3;-2;1).
(-3;-2;1).
6.  (1;2;5),
(1;2;5),  (2;-3;4),
(2;-3;4),  (1;-1;-2),
(1;-1;-2),  (3;0;1).
(3;0;1).
7.  (5;1;2),
(5;1;2),  (3;4;-1),
(3;4;-1),  (-4;2;1),
(-4;2;1),  (-3;5;4).
(-3;5;4).
8.  (2;1;5),
(2;1;5),  (-4;3;5),
(-4;3;5),  (1;-1;-4),
(1;-1;-4),  (4;-1;-3).
(4;-1;-3).
9.  (3;1;4),
(3;1;4),  (-4;2;3),
(-4;2;3),  (2;-1;-2),
(2;-1;-2),  (7;-1;0).
(7;-1;0).
10.  (1;4;2),
(1;4;2),  (5;-2;-3),
(5;-2;-3),  (-2;-1;1),
(-2;-1;1),  (-3;2;4).
(-3;2;4).
11.  (2;1;3),
(2;1;3),  (3;-2;1),
(3;-2;1),  (1;-3;-4),
(1;-3;-4),  (7;0;7).
(7;0;7).
12.  (5;3;1),
(5;3;1),  (-2;-1;2),
(-2;-1;2),  (-2;1;4),
(-2;1;4),  (3;0;1).
(3;0;1).
13.  (1;3;5),
(1;3;5),  (-2;-1;-1),
(-2;-1;-1),  (4;-2;4),
(4;-2;4),  (-7;3;-1).
(-7;3;-1).
14.  (3;1;6),
(3;1;6),  (-2;2;-3),
(-2;2;-3),  (-4;5;-1),
(-4;5;-1),  (3;0;1).
(3;0;1).
15.  (4;1;4),
(4;1;4),  (-2;-1;1),
(-2;-1;1),  (3;1;5),
(3;1;5),  (-3;-2;1).
(-3;-2;1).
16.  (1;2;5),
(1;2;5),  (2;-3;4),
(2;-3;4),  (1;-1;-2),
(1;-1;-2),  (3;0;1).
(3;0;1).
17.  (5;1;2),
(5;1;2),  (3;4;-1),
(3;4;-1),  (-4;2;1),
(-4;2;1),  (-3;5;4).
(-3;5;4).
18.  (2;1;5),
(2;1;5),  (-4;3;5),
(-4;3;5),  (1;-1;-4),
(1;-1;-4),  (4;-1;-3).
(4;-1;-3).
19.  (3;1;4),
(3;1;4),  (-4;2;3),
(-4;2;3),  (2;-1;-2),
(2;-1;-2),  (7;-1;0).
(7;-1;0).
20.  (1;4;2),
(1;4;2),  (5;-2;-3),
(5;-2;-3),  (-2;-1;1),
(-2;-1;1),  (-3;2;4).
(-3;2;4).
Задание 7
В задачах 1 – 20 найти указанные пределы.
1. а) 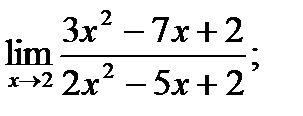 б)
б) 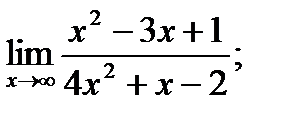
в) 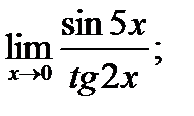 г)
г) 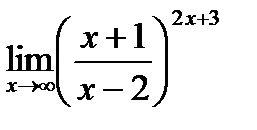
2. а) 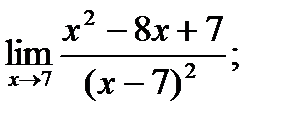 б)
б) 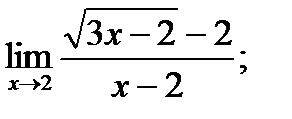
в) 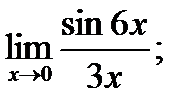 г)
г) 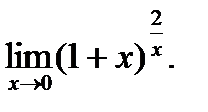
3. а) 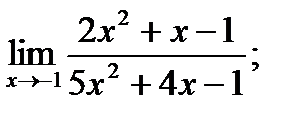 б)
б) 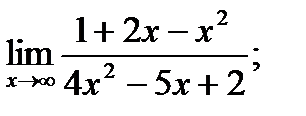
в) 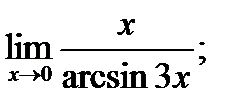 г)
г) 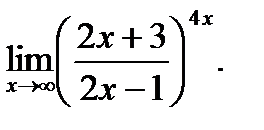
4. а) 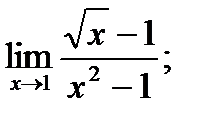 б)
б) 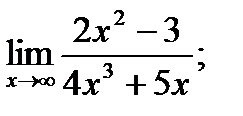
в) 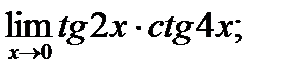 г)
г) 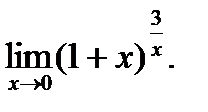
5. а) 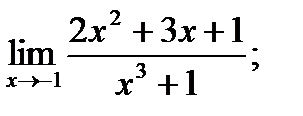 б)
б) 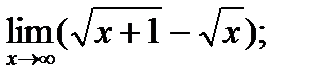
в) 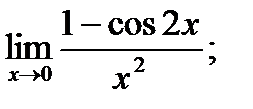 г)
г) 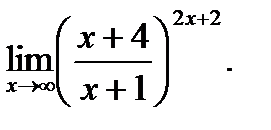
6. а) 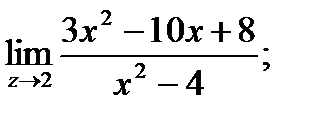 б)
б) 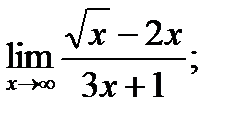
в) 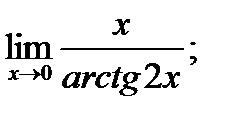 г)
г) 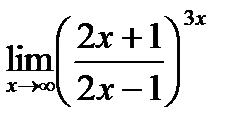 .
.
7. а) 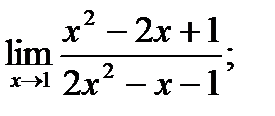 б)
б) 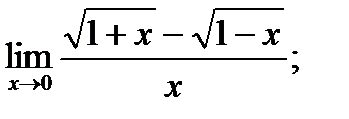
в) 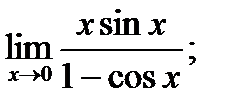 б)
б) 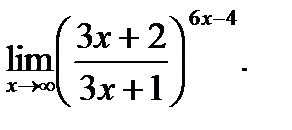
8. а) 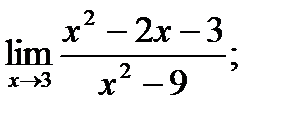 б)
б) 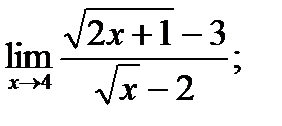
в) 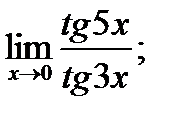 г)
г) 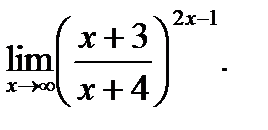
9. a) 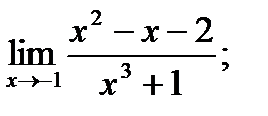 б)
б) 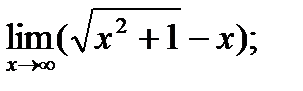
в) 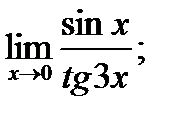 г)
г) 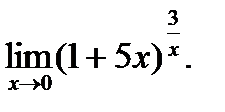
10. а) 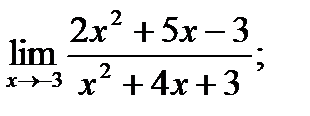 б)
б) 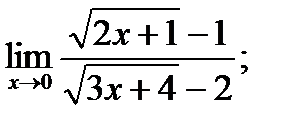
в) 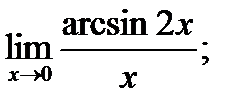 г)
г) 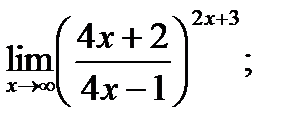
11. а) 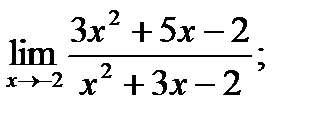 б)
б) 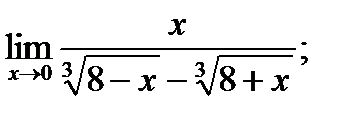
в) 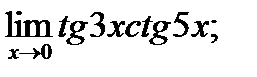 г)
г) 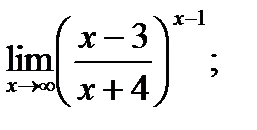
12. а) 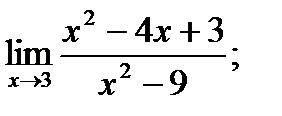 б)
б) 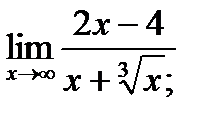
в) 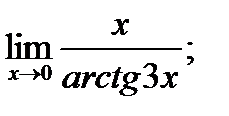 г)
г) 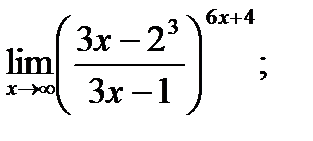
13. а) 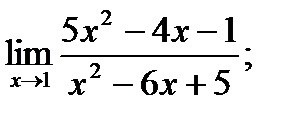 б)
б) 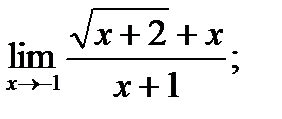
в) 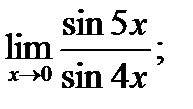 г)
г) 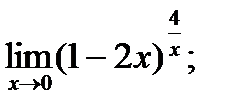
14. а) 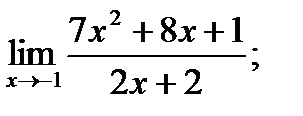 б)
б) 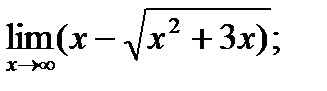
в) 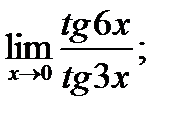 г)
г) 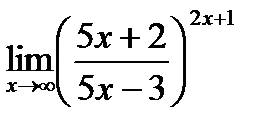
15. а) 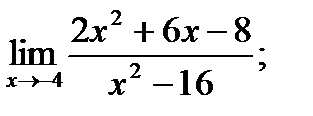 б)
б) 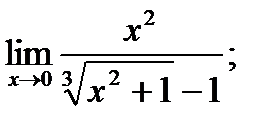
в) 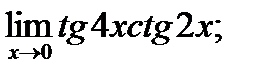 г)
г) 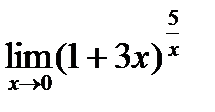
16. а) 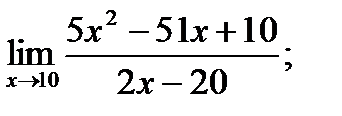 б)
б) 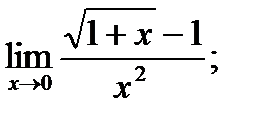
в) 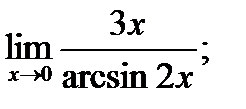 г)
г) 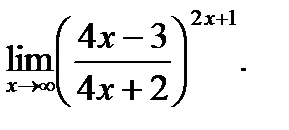
17. а) 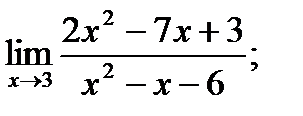 б)
б) 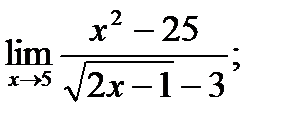
в) 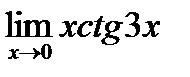 ; г)
; г) 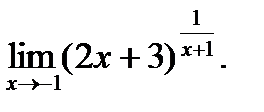
18. а) 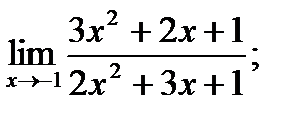 б)
б) 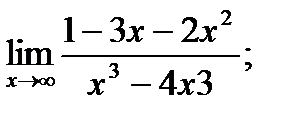
в) 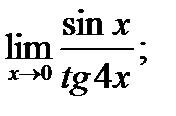 г)
г) 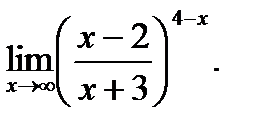
19. а) 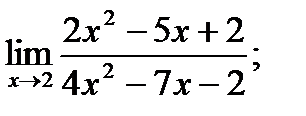 б)
б) 
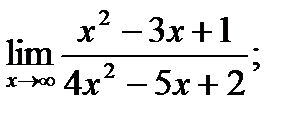
в) 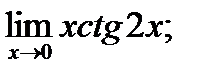 г)
г) 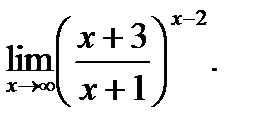
20. а) 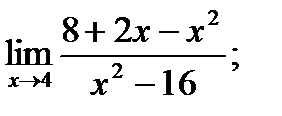 б)
б) 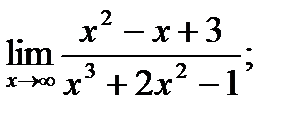
в) 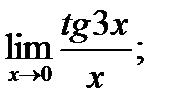 г)
г) 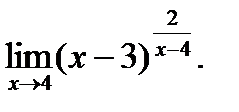
Задание 8
В задачах 1 – 20 найти производные заданных функций:
1. а) 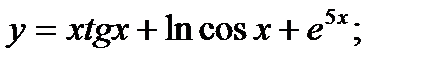 б)
б) 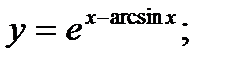 в)
в) 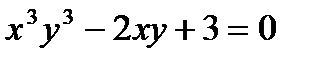 .
.
2. а) 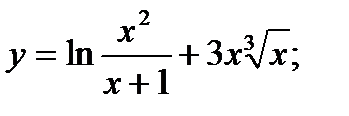 б)
б) 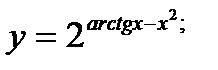 в)
в) 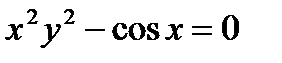 .
.
3. а) 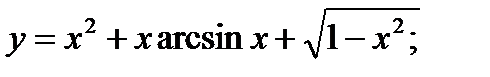 б)
б) 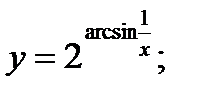 в)
в) 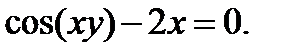
4. а) 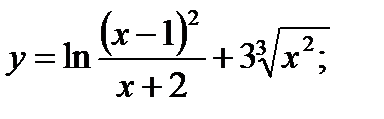 б)
б) 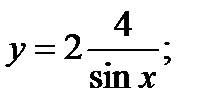 в)
в) 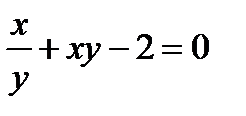 .
.
5. а) 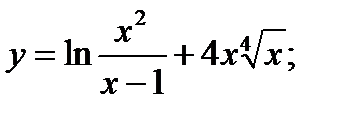 б)
б) 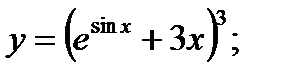 в)
в) 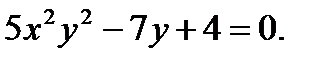
6. а) 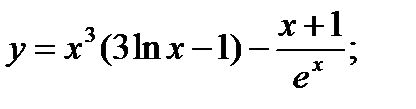 б)
б) 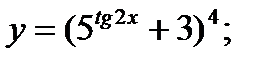 в)
в) 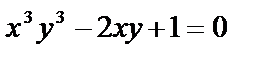 .
.
7. а) 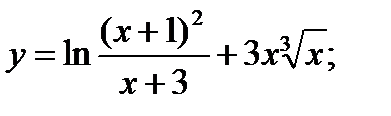 б)
б) 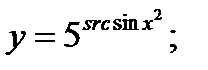 в)
в) 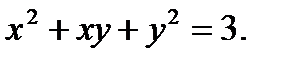
8. а) 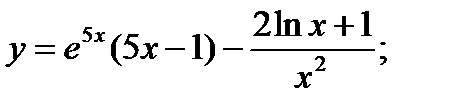 б)
б) 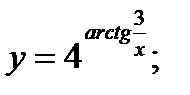 в)
в) 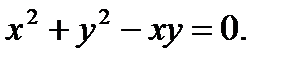
9. а) 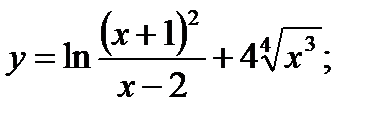 б)
б) 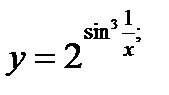 в)
в) 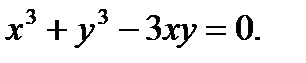
10. а) 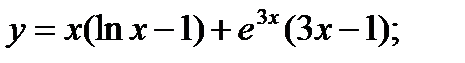 б)
б) 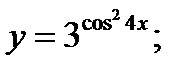 в)
в) 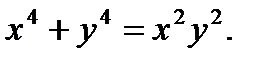
11. а) 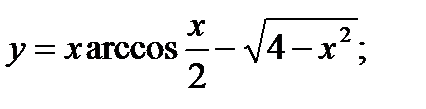 б)
б) 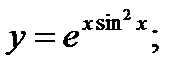 в)
в) 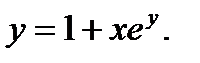
12. а) 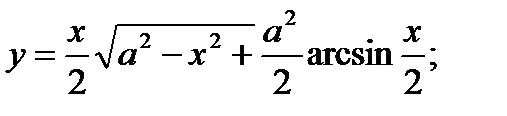 б)
б) 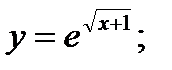 в)
в) 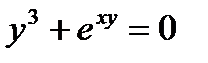 .
.
13. а) 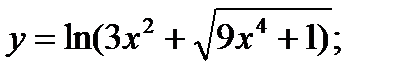 б)
б) 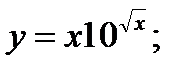 в)
в) 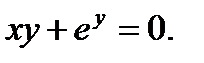
14. а) 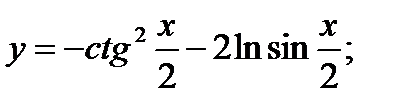 б)
б) 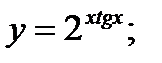 в)
в) 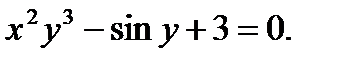
15. а) 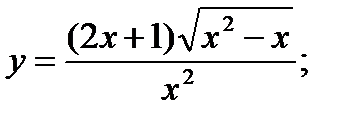 б)
б) 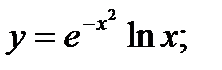 в)
в) 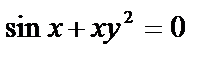
16. а) 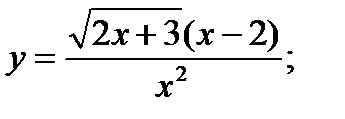 б)
б) 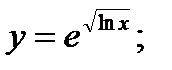 в)
в) 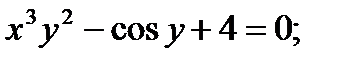
17. а) 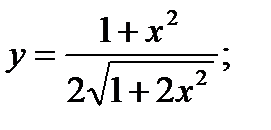 б)
б) 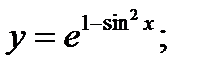 в)
в) 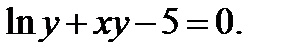
18. а) 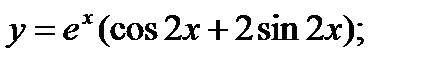 б)
б) 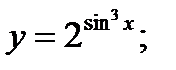 в)
в)
