Решение систем линейных уравнений методами Крамера и Гаусса

Пусть дана система n уравнений с n неизвестными:

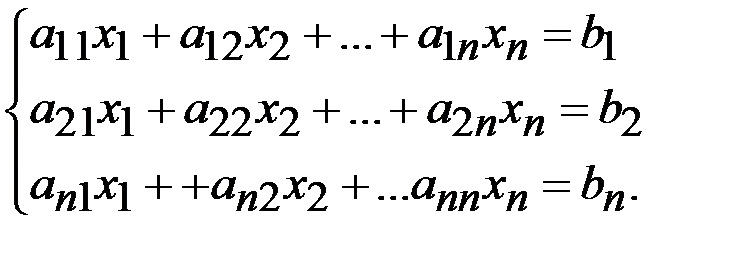
Основная матрица А такой системы квадратная. Определитель этой матрицы

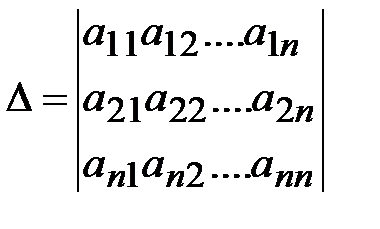
называется определителем системы.

Если определитель системы отличен от нуля, то система называется невырожденной и имеет единственное решение.

В дальнейшем мы будем иметь дело только с такими системами.

Наиболее простым методом для решения таких систем линейных уравнений является метод Крамера.

Формулы Крамера имеют вид:

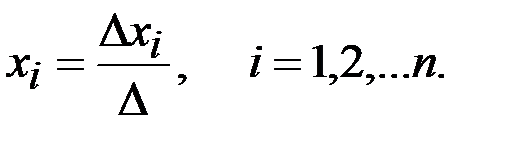
Более универсальным и эффективным является метод Гаусса, состоящий в последовательном исключении неизвестных.

Решение осуществляется в два этапа: 1) система приводится к треугольному виду, 2) последовательно определяют неизвестные .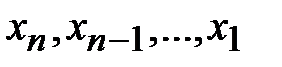

Задача 1.

Решить систему уравнений методами Крамера и Гаусса:

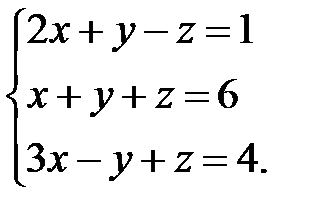
Решение:

а) Метод Крамера.

Найдем определитель системы . Предварительно сложив второй столбец с третьим и разложив определитель по элементам последнего столбца.

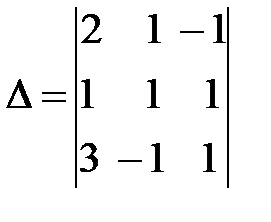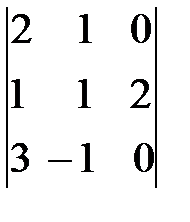= =2(-1)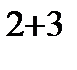 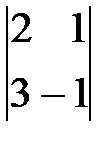=-2(-2-3)=10 .

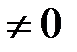Так как 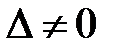, то система имеет единственное решение.

Найдем определител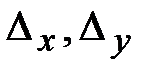и и 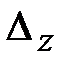, заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов (при вычислении определителя 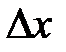выполним преобразования аналогичные предыдущему.)

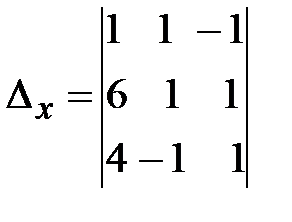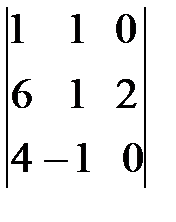= =2(-1)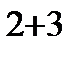 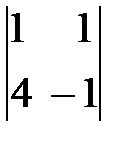-2(-1-4)=10.

При вычислении определителя 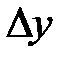последнюю строку складываем с первой и вычитаем из второй строки. Разлагаем по элементам последнего столбца.

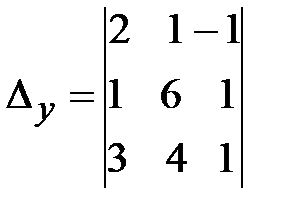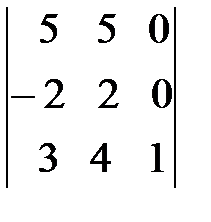= =1(-1)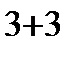 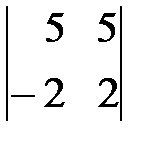=10+10=20.

При вычислении определителя 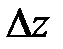последнюю строку складываем с первой и со второй строки и разлагаем получившийся определитель по элементам второго столбца.

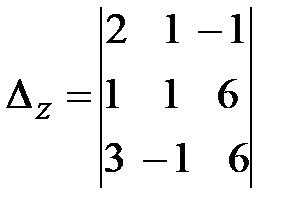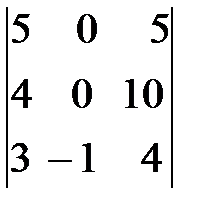= =-1(-1)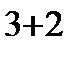 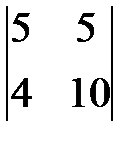=50-20=30.

Подставляя найденные значения в формулы Крамера, получим:

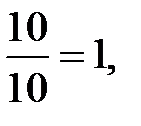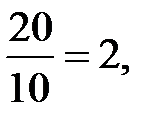Х = у = z =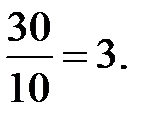

б) Метод Гаусса.

Составим расширенную матрицу системы:

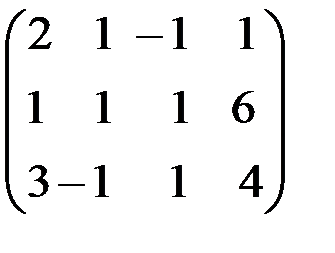
Разрешающим элементом 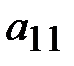удобно иметь единицу, поэтому переставим второе уравнение на место первого.

Получим нули в первом столбце, умножив первое уравнение последовательно на (-2) и (-3) и складывая со вторым и третьим.

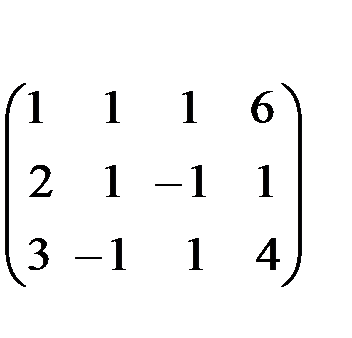(-2) (-3)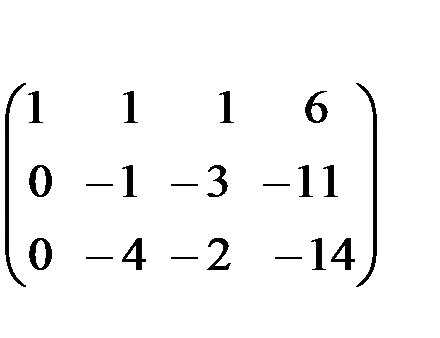

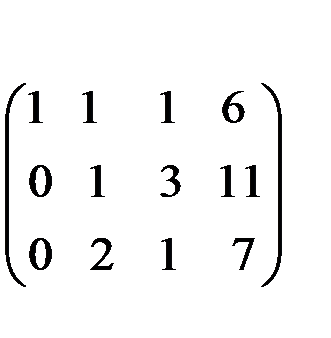
С помощью второго элемента второй строки сделаем нуль во втором столбце третьей строки, для чего умножим вторую строку на (-2) и сложим с третьей.

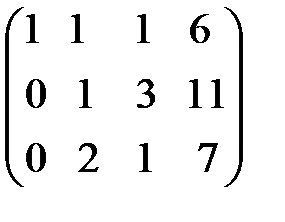(-2) .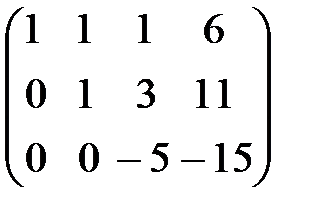

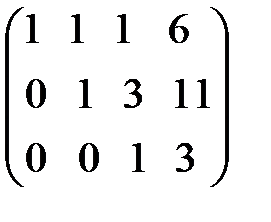Таким образом, свели матрицу к треугольному виду. Запишем полученную систему уравнений:

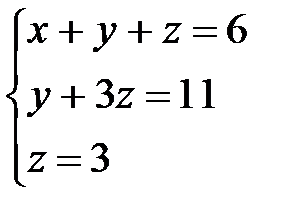
Из последнего уравнения сразу находим значение z=3, подставляя которое во второе уравнение находим у=11-3z=11-9=2. Затем из первого уравнения найдем

х=1, у=2, z=3.

Задача 2. Данную систему уравнений записать в матричной форме и решить ее c помощью обратной матрицы:

x₁— 2х₂+x₃=1,

2x₁+3х₂ — x₃=8

x₁ — х₂+2х₃=- 1

Решение. Обозначим через А матрицу коэффициентов при неизвестных; Х — матрицу-столбец неизвестных Х₁, X₂, X₃; H - матрицу-столбец свободных членов:

1 -2 1 X₁ 1

А= 2 3 -1 , Х= Х₂ H= 8 .

1 -1 2 X₃ -1

С учетом этих обозначений данная система уравнений принимает следующую матричную форму: A× Х=Н (l)

Если матрица А — невырожденная (ее определитель отличен от нуля), то она имеет обратную матрицу А^-1. Умножив обе части уравнения (1) на А^-1 слева получим:

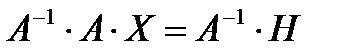
Но 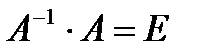(Е — единичная матрица), а ЕХ=Х, Поэтому

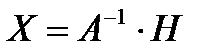(2)

Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А^-1.

Пусть имеем невырожденную матрицу

а₁₁ а₁₂ а₁₃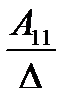

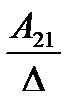
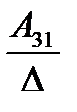
А= а₂₁ а₂₂ а₂₃ . Тогда А^-1=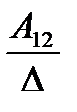

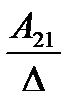
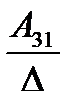
а₃₁ а₃₂ а₃₃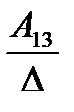

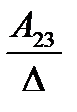
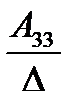
где А_ij (i=1, 2, 3; j=l, 2, 3) — алгебраическое дополнение элемента а_ij в определителе матрицы А, которое является произведением (-l)^i+j на минор (определитель) второго порядка, полученный вычерчиванием i-й строки и j-гo столбца в определителе матрицы А.

Вычислим определитель и алгебраические дополнения А_ij элементов матрицы А.

1 -2 1

= 2 3 -1 =10 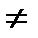0, следовательно, матрица А имеет обратную матрицу А^-1

1 -1 2

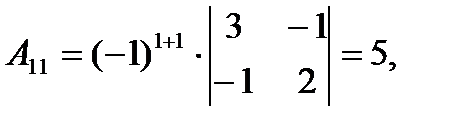
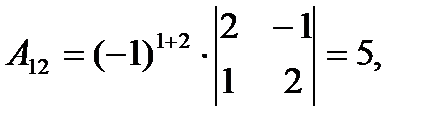
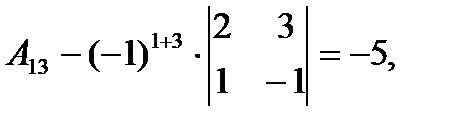
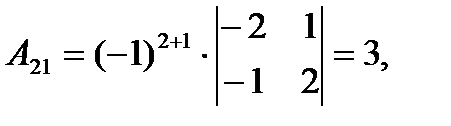
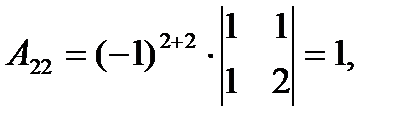
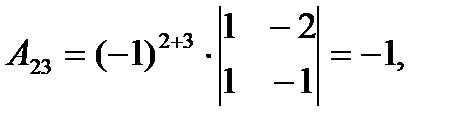
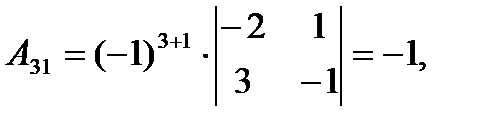
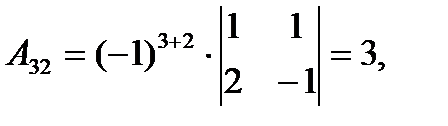
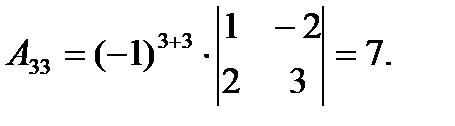
Тогда

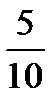
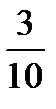
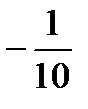5 3 -1

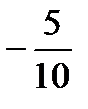
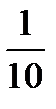
А^-1= 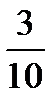= 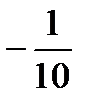-5 1 3

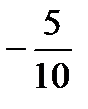
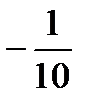
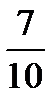-5 -1 7

По формуле (2) находим решение данной системы уравнений в матричной форме:

= ×

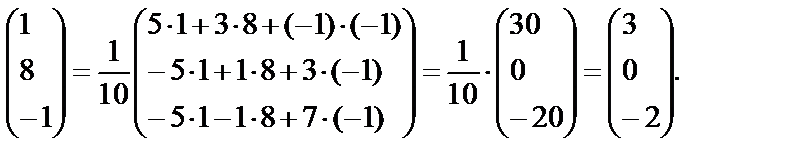
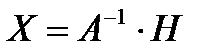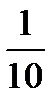
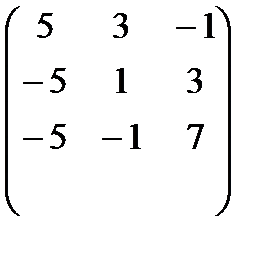Отсюда x₁=3, x₂ =0, x₃=-2