ТЕМА 1. Элементы линейной алгебры
ТЕМА 1. Элементы линейной алгебры
Лекция № 1
Тема: Общие понятия системы линейных уравнений.
Тема: Матрицы и определители
1. Понятие матрицы. Виды Матриц.
2. Действия над матрицами.
3. Виды определителей и правила их вычисления.
4. Минор, алгебраическое дополнение.
Понятие матрицы. Виды Матриц.
Определение.Матрицей размера m  n называется прямоугольная таблица чисел, содержащая mстрок и n столбцов.
n называется прямоугольная таблица чисел, содержащая mстрок и n столбцов.
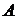 =
= 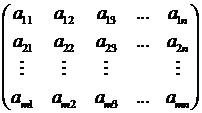 или
или 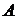 =
= 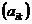 ,
, 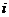 =1,2,…,
=1,2,…, 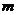 ,
, 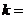 1,2,…,
1,2,…, 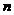 .
.
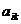 – элемент матрицы, стоящий на пересечении
– элемент матрицы, стоящий на пересечении 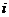 -й строки и
-й строки и 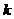 -го столбца.
-го столбца.
Определение. Если 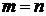 , то матрица называется квадратнойn-го порядка, в противном случае – прямоугольной.
, то матрица называется квадратнойn-го порядка, в противном случае – прямоугольной.
Элементы 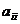 ,
, 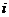 = 1, 2, …, n квадратной матрицыА образуют ее главную диагональ.
= 1, 2, …, n квадратной матрицыА образуют ее главную диагональ.
Матрица размера 1хn называется матрицей-строкой, а матрица размера 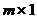 – матрицей-столбцом.
– матрицей-столбцом.
Определение. Две матрицы называются равными, если они имеют одинаковый размер и равны их элементы, стоящие на одинаковых местах.
Определение. Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали, то есть 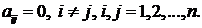
На главной диагонали могут быть любые числа. Если все они равны 1, то диагональная матрица называется единичной и обозначается буквой 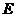 .
.
Определение. Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.

Действия над матрицами
Сложение и вычитание матриц
Складывать и вычитать можно матрицы одного размера в результате получается матрица того же размера.
Определение.Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:
сij = aij + bij
Определение.Вычитание матриц (разность матриц) A - B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц A и B, то есть каждый элемент матрицыC равен:
сij = aij - bij
Примеры задач на сложение и вычитание матриц
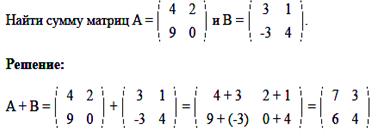
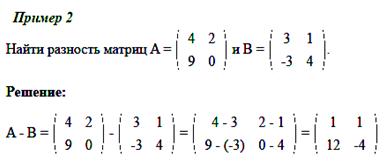
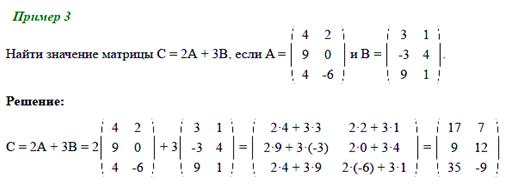
Умножение матриц
Определение.Результатомумножения матрицAm×nиBn×kбудет матрицаCm×kтакая, что элементматрицыC, стоящий вi-той строке иj-том столбце (cij), равен сумме произведений элементов i-той строки матрицыAна соответствующие элементыj-того столбца матрицыB:
 cij = ai1 · b1j + ai2 · b2j + ... + ain · bnj
cij = ai1 · b1j + ai2 · b2j + ... + ain · bnj
Замечание.Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.
Свойства умножения матриц
- (A · B) · C= A · (B · C) - произведение матриц ассоциативно;
- (z · A) · B=z · (A · B), гдеz - число;
- A · (B + C) = A · B + A · C - произведение матриц дистрибутивно;
- En· Anm= Anm· Em= Anm- умножение наединичную матрицу;
- A · B ≠ B · A - в общем случае произведение матриц не коммутативно.
- Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.
Примеры на умножение матриц
Пример 1.
| Найти матрицу C равную произведению матриц A = |  |  | и B = |  | 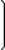 | . | ||||
| -3 |
Решение:
| С = A · B = |  | 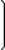 | · |  | 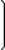 | = |  | 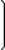 | ||||||
| -3 |
Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 4·3 + 2·(-3) = 12 - 6 = 6
c12 = a11·b12 + a12·b22 = 4·1 + 2·4 = 4 + 8 = 12
c21 = a21·b11 + a22·b21 = 9·3 + 0·(-3) = 27 + 0 = 27
c22 = a21·b12 + a22·b22 = 9·1 + 0·4 = 9 + 0 = 9
Пример 2.
| Найти матрицу C равную произведению матриц A = |
| и B = |
| . |
Решение:
| C = A · B = |
| · |
| = |
|
Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 2·5 + 1·(-3) = 10 - 3 = 7
c12 = a11·b12 + a12·b22 = 2·(-1) + 1·0 = -2 + 0 = -2
c13 = a11·b13 + a12·b23 = 2·6 + 1·7 = 12 + 7 = 19
c21 = a21·b11 + a22·b21 = (-3)·5 + 0·(-3) = -15 + 0 = -15
c22 = a21·b12 + a22·b22 = (-3)·(-1) + 0·0 = 3 + 0 = 3
c23 = a21·b13 + a22·b23 = (-3)·6 + 0·7 = -18 + 0 = -18
c31 = a31·b11 + a32·b21 = 4·5 + (-1)·(-3) = 20 + 3 = 23
c32 = a31·b12 + a32·b22 = (4)·(-1) + (-1)·0 = -4 + 0 = -4
c33 = a31·b13 + a32·b23 = 4·6 + (-1)·7 = 24 - 7 = 17
Определение.Транспонирование матрицы - это операция над матрицей, при которой ее строки и столбцы меняются местами:
(aij) T= aji
Определение. Обратная матрица A−1 - матрица, произведение которой на исходную матрицу A равно единичной матрице E:
A·A-1 = A-1·A = E
Обратная матрица для матрицы 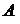
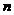 - го порядка имеет вид:
- го порядка имеет вид:
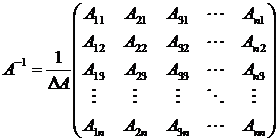 .
.
Замечание.Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.
Теорема. Всякая невырожденная матрица имеет обратную, причем одну.
Определение. Квадратная матрица 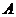 называется невырожденной, если
называется невырожденной, если 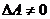 . Если
. Если 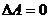 , то
, то 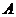 называется вырожденной.
называется вырожденной.
Пример. 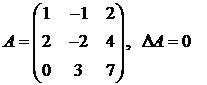 по свойству 6 определителей, то есть
по свойству 6 определителей, то есть 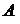 – вырожденная.
– вырожденная.
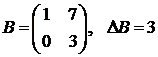 , значит,
, значит, 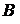 – невырожденная.
– невырожденная.
Пример. Найти матрицу, обратную для 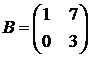 .
.
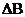 =3
=3 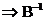 существует.
существует. 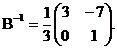

Проверка:
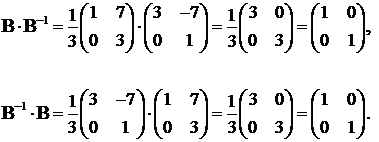
Лекция № 2.
Тема: Решение систем линейных уравнений
План:
1. Формулы Крамера.
2. Метод обратной матрицы.
3. Метод Гаусса.
Формулы Крамера.
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений.
Теорема. Система из n уравнений с n неизвестными
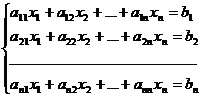
в случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам: xi = 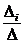 где D = detA, а Di – определитель матрицы, получаемой из матрицы системы заменой столбцаi столбцом свободных членов bi.
где D = detA, а Di – определитель матрицы, получаемой из матрицы системы заменой столбцаi столбцом свободных членов bi.
Di = 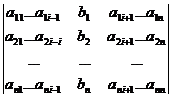
Пример. Найти решение системы уравнений: 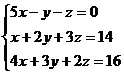
D = 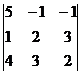 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = 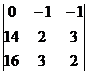 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = 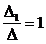
D2 = 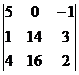 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = 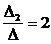
D3 = 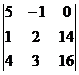 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = 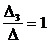
Замечание 1. Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
Замечание 2. При D = 0 система имеет бесконечное множество решений.
Метод обратной матрицы.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Пусть дана система уравнений: 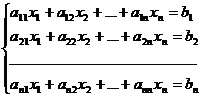 Составим матрицы:
Составим матрицы:
A = 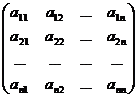 - матрица коэффициентов при переменных или матрица системы;
- матрица коэффициентов при переменных или матрица системы;
B =  - матрица –столбец свободных членов;
- матрица –столбец свободных членов;
X =  - матрица – столбец неизвестных.
- матрица – столбец неизвестных.
Тогда систему уравнений можно записать:A×X = B.Домножим слева обе части равенства на A-1: A-1×A×X = A-1×B, т.к. А-1×А = Е, то Е×Х = А-1×В, то справедлива следующая формула:
Х = А-1×В
Таким образом, для применения данного метода необходимо находить обратную матрицу.
Пример. Решить систему уравнений: 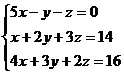
Х = 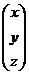 , B =
, B = 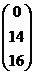 , A =
, A = 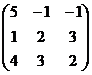
Найдем обратную матрицу А-1.
D = detA = 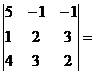 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ обратная матрица существует.
5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ обратная матрица существует.
M11= 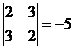 ; M21 =
; M21 = 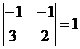 ; M31 =
; M31 = 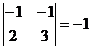 ;
;
M12 = 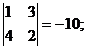 M22 =
M22 = 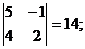 M32 =
M32 = 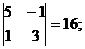
M13 = 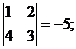 M23 =
M23 = 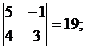 M33 =
M33 = 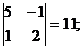
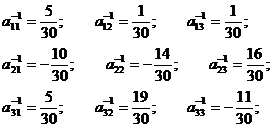
A-1= 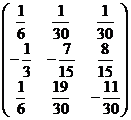 ;
;
Cделаем проверку:
A×A-1 = 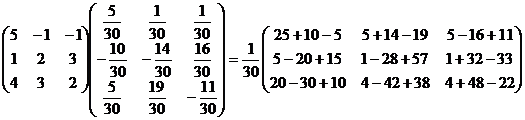 =E.
=E.
Находим матрицу Х.
Х = 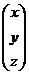 = А-1В =
= А-1В = 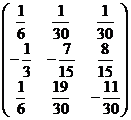 ×
× 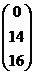 =
= 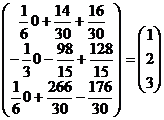 .
.
Получили решения системы: x =1; y = 2; z = 3.
3.Метод Гаусса.
Пусть дана система m линейных уравнений с n неизвестными:
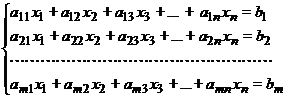
Полагая, что в системе коэффициент a11 отличен от нуля (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x1). Преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x1 с помощью эквивалентных преобразований описанным выше способом.
В полученной системе

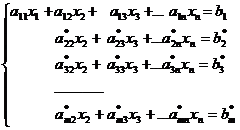 ,
,
считая, что 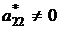 (что всегда можно получить, переставив уравнения или слагаемые внутри уравнений), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x2. Во вновь полученной системе
(что всегда можно получить, переставив уравнения или слагаемые внутри уравнений), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x2. Во вновь полученной системе
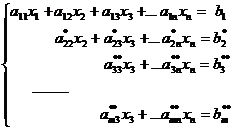
при условии 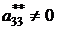 оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x3.
оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x3.
Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:
1)если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;
2)если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;
3)если получается ступенчатая система коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.
Рассмотрим квадратную систему: 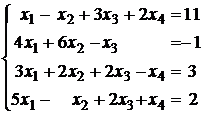 (1)
(1)
У этой системы коэффициент a11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю.
Проведем следующие преобразования системы:
1) поскольку a11¹0, первое уравнение оставим без изменений;
2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;
3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;
4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.
Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x1 (это и являлось целью преобразований 1 – 4): 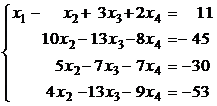 (2)
(2)
Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде матрицы
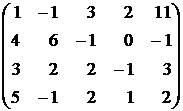 . (3)
. (3)
Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы.
Системе (2) соответствует расширенная матрица
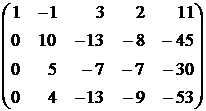 .
.
Преобразуем эту матрицу следующим образом:
1) первые две строки оставим без изменения, поскольку элемент a22 не равен нулю;
2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;
3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.
В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
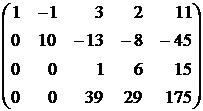 .
.
Теперь исключим неизвестную x3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так:
1) первые три строки оставим без изменения, так как a33¹ 0;
2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой: 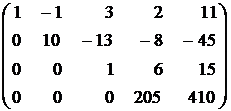 .
.
Полученная матрица соответствует системе
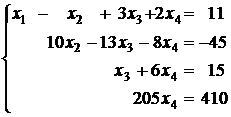 . (4)
. (4)
Из последнего уравнения этой системы получаем x4 = 2. Подставив это значение в третье уравнение, получим x3 = 3. Теперь из второго уравнения следует, что x2 = 1, а из первого — x1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x4, затем x3 и т. д.).
Определение: Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей.
Матрица коэффициентов системы (4) – треугольная матрица.
Лекция № 3.
Тема:Векторы. Скалярное, векторное и смешанное произведение векторов
План:
1. Понятие вектора. Коллинарность, компланарность векторов.
2. Линейные операции над векторами.
3. Скалярное произведение векторов
4. Векторное произведение векторов
5. Смешанное произведение векторов
1. Понятие вектора.Коллинарность, компланарность векторов.
| |
 с начальной точкой А и конечной точкой В.
с начальной точкой А и конечной точкой В. Обозначение:  ,
, 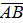 ,
, 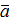
Определение: Длиной или модулем вектора 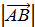 вектора
вектора 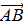 называется число, равное длине отрезка АВ, изображающего вектор.
называется число, равное длине отрезка АВ, изображающего вектор.
Определение: Вектор называется нулевым, если начало и конец вектора совпадают.
Определение: Вектор единичной длины называется единичным.
Определение: Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( 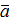 ||
|| 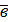 ).
).
Замечание:
1.Коллинеарные векторы могут быть направлены одинаково или противоположно.
2. Нулевой вектор считается коллинеарным любому вектору.
Определение: Два вектора называются равными, если они коллинеарные,
одинаково направлены и имеют одинаковые длины (  =
= 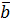 )
)
Определение: Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях
2. Линейные операции над векторами:
Произведением вектора 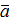 на число λ называется вектор
на число λ называется вектор 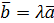 , имеющий длину
, имеющий длину 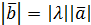 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора 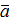 , если λ>0, и противоположно ему, если λ<0
, если λ>0, и противоположно ему, если λ<0
Противоположным вектором –  называется произведение вектора
называется произведение вектора  на число (-1), т. е. –
на число (-1), т. е. –  =(-1)
=(-1) 
Суммой двух векторов  и
и 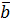 называется вектор
называется вектор 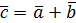 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора 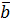 , при условии, что начало вектора
, при условии, что начало вектора 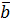 совпадает с концом вектора
совпадает с концом вектора  (правило треугольников)
(правило треугольников)
Сумму двух векторов можно построить также по правилу параллелограмма, где вектор 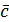 представляет собой диагональ параллелограмма
представляет собой диагональ параллелограмма
Аналогично определяется сумма нескольких векторов.
Например, суммой четырех вектор 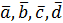 является вектор
является вектор 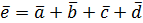 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора 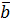 (правило многоугольника)
(правило многоугольника)
Вектор 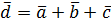 , определяемый таким образом, представляет собой диагональ параллелепипеда, построенного на векторах
, определяемый таким образом, представляет собой диагональ параллелепипеда, построенного на векторах 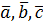 , не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда)
, не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда)
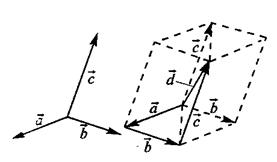
Разностью двух векторов 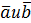 называется сумма вектора
называется сумма вектора  и вектора
и вектора 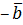 , противоположного
, противоположного 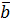 (можно вычитать векторы по правилу
(можно вычитать векторы по правилу 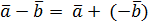 , т. е. вычитание векторов заменить сложением вектора
, т. е. вычитание векторов заменить сложением вектора  с вектором, противоположным вектору
с вектором, противоположным вектору 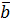 )
)
Замечание: в параллелограмме, построенном на векторах 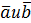 , одна направленная диагональ является суммой этих векторов, а другая – разностью.
, одна направленная диагональ является суммой этих векторов, а другая – разностью.
Определение: Координатами вектора 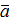 называются координаты его конечной точки.
называются координаты его конечной точки.
|
 (x, y)), а в пространстве Oxyz – три числа x, y, z (
(x, y)), а в пространстве Oxyz – три числа x, y, z (  (x, y, z))
(x, y, z)) | |
Лекция № 4.
Тема:Прямая линия на плоскости
1. Виды уравнений прямой на плоскости.
Общее уравнение прямой
Имеет вид Ax+By+C=0, где А и В – одновременно не равны 0
Определение.Уравнением линии называется такое уравнение, которому удовлетворяют координаты всех точек, лежащих на этой линии, и не удовлетворяют координаты ни одной точки, не лежащей на линии
Обозначение: В общем виде F(x, y)=0 или y=f(x) (если возможно),
где F(x, y), f(x) – некоторые функции
1. Уравнение прямой с угловым коэффициентом
имеет вид y=kx+b,где k-угловой коэффициент прямой, равный k=tgα
Тема:Плоскость и прямая в пространстве
1. Виды уравнений плоскости в пространстве.
Пусть точка Mo(x0,y0,z0) лежит на плоскости и вектор 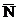 (A,B,C) перпендикулярен к плоскости (рис.1)
(A,B,C) перпендикулярен к плоскости (рис.1)
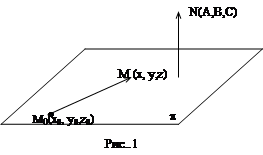 |
Возьмём на плоскости p любую точку M(x,y,z), образуем вектор 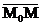 и используем условие перпендикулярности двух векторов
и используем условие перпендикулярности двух векторов 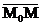 и
и 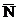 .
.
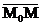 ^
^ 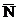 Þ (
Þ ( 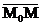 ,
, 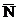 ) = 0
) = 0
Запишем уравнение данное уравнение в координатной форме.
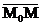 (x0-x, y0-y, z-z0),
(x0-x, y0-y, z-z0), 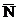 (A, B, C)
(A, B, C)
( 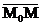 ,
, 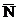 ) = A(x-x0) + B(y0-y) + C(z-z0)
) = A(x-x0) + B(y0-y) + C(z-z0)
Преобразуя последнее выражение, получим Ax+By+Cz+D=0, где
D=-Ax0-By0-Cz0
Уравнение Ax+By+Cz+D=0 называется общим уравнением плоскости в пространстве.
Лекция № 5.
Тема:Функции и их свойства. Предел последовательности и функции.
План:
1. Функции и их свойства.
2. Числовая последовательность.
3. Предел функции в точке.
4. Предел функции на бесконечности.
5. Основные теоремы о пределах.
6. Замечательные пределы.
Функции и их свойства.
Определение: Пусть заданы некоторые числовые множества X, Y.
Если каждому элементу x множества X ставиться в соответствие определенный элемент y множества Y, то говорят, что на множестве X задана функция y=f(x).
Переменная x называется независимой переменной или аргументом, y – зависимой или функцией
Множество X – область допустимых значений независимой переменной x, множество Y- множество значений функции.
Определение: Графиком функции y=f(x) называется множество всех точек плоскости Oxy, для каждой из которых x является значением аргумента, а y соответствующим значением функции.
Способы задания функции:
1. Аналитический способ. При этом способе указывается формула, связывающая зависимую переменную величину с независимой переменной величиной.
2. Табличный способ. При этом способе выписываются в определенном порядке значения аргумента x1, x2, x3…xn и соответствующие значения функции y1, y2, y3…yn
| x | x1 | x2 | … | xn |
| y | y1 | y2 | … | yn |
3. Графический способ. Этот способ удобен, когда задать функцию аналитически довольно трудно. Этот способ состоит в изображении графика функции – т. е. множества точек (x, y) плоскости, абсциссы которых есть значения аргумента x, ординаты – соответствующие им значения функции y=f(x).
4. Словесный способ. Функция описывается правилом составления.
Основные свойства функции:
1. Четность и нечетность функции.
Определение: Функция y=f(x) называется четной, если при всех значениях x из области определения этой функции выполняется условие f(-x)=f(x).
Определение: Функция y=f(x) называется нечетной, если при всех значениях x из области определения этой функции выполняется условие f(-x)=-f(x).
Замечание: Если функция не является не четной и не нечетной, то функция является функцией общего вида.
2. Монотонность функции.
Определение: Функция y=f(x) называется монотонно возрастающей (возрастающей) на множестве X, если большему значению аргумента из этого промежутка соответствует большее значение функции, т. е. для x1, x2ϵX и x2>x1, следовательно, f(x2)>f(x1)
Определение: Функция y=f(x) называется монотонно убывающей (убывающей) на множестве X, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т. е. для x1, x2ϵX и x2>x1, следовательно, f(x2)<f(x1)
Функции возрастающие и убывающие называются монотонными функциями.
3. Ограниченность функции.
Определение: Функция y=f(x) называется ограниченной на промежутке X, если существует такое положительное число М>0, что |f(x)|≤M для любого xϵM. В противном случае, функция называется неограниченной.
4. Периодичностьфункции.
Определение: Функция y=f(x) называется периодической, если существует число Т≠0, такое, что при любых x из области определения функции выполняется условие f(x+T)=f(x). Число Т называется периодом функции.
Предел функции в точке.
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
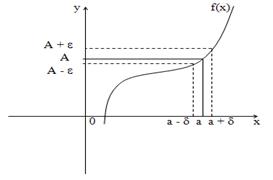
Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число d>0, что для всех х таких, что
0 <ïx - aï<d верно неравенствоïf(x) - Aï<e.
Обозначение: 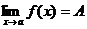
Определение.Если f(x) ®A1 при х ® а только при x<a, то 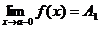 - называется пределом функции f(x) в точке х = а слева, а если f(x) ®A2 при х ® а только при x>a, то
- называется пределом функции f(x) в точке х = а слева, а если f(x) ®A2 при х ® а только при x>a, то 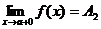 называется пределом функции f(x) в точке х = а справа.
называется пределом функции f(x) в точке х = а справа.
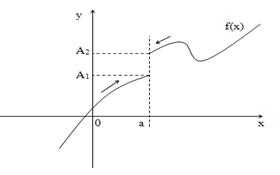
Данное определение справедливо для функции f(x), которая не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.
Пределы А1 и А2 называются односторонними пределами функции f(x) в точке х = а.
Замечательные пределы.
Первый замечательный предел 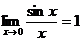
Второй замечательный предел 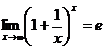
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме, изложенных выше, пределов можно записать следующие полезные на практике соотношения: 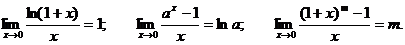
Пример. Найти предел: 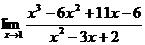 .
.
Решение: если напрямую подставить вместо х предельное значение 1, тогда вверху и внизу получатся 0 – это называется неопределенностью (записывается как 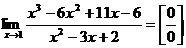 ) и эту неопределенность необходимо раскрыть чтобы решить предел (вычислить, т.е. получить ответ в виде числа). Для раскрытия неопределенностей такого вида сделаем следующее:
) и эту неопределенность необходимо раскрыть чтобы решить предел (вычислить, т.е. получить ответ в виде числа). Для раскрытия неопределенностей такого вида сделаем следующее:
1) Разложим числитель и знаменатель,данной дроби на множители. В знаменателе по правилам нахождения корней квадратного уравнения, т.е.ах2 + bх + с = 0- квадратное уравнение в общем виде, где а,b, с – коэффициенты уравнения (произвольные числа)

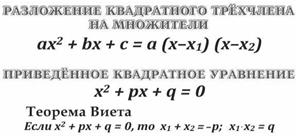 т.е. для
т.е. для 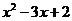 = 0, получим корни х1 = 1, х2 = 2. А в числителе по правилам нахождения корней кубического уравнения:
= 0, получим корни х1 = 1, х2 = 2. А в числителе по правилам нахождения корней кубического уравнения: 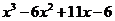 = 0
= 0
2) Запишем предел следующим образом 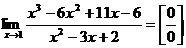 =
= 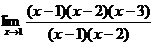
3) сокращаем одинаковые скобки, получаем
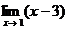
следовательно, неопределенность раскрыта и
4) можно подставить предельное значение на место х, т.е. 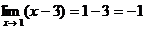 .
.
Пример. Найти предел: 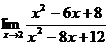 .
.
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби по правилам нахождения корней квадратного уравнения, т.е.
ах2 + bх + с = 0- квадратное уравнение в общем виде, где а,b, с – коэффициенты уравнения (произвольные числа)

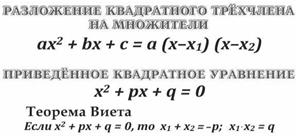
Т.е. 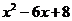 = 0 и находим корни х1 = 2, х2 = 4, следовательно, разложением на множители получим:
= 0 и находим корни х1 = 2, х2 = 4, следовательно, разложением на множители получим: 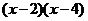 . Аналогично для знаменателя:
. Аналогично для знаменателя: 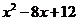 = 0 получим:
= 0 получим: 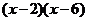 .
.
Тогда 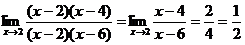 .
.
Пример. Найти предел: 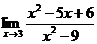 .
.
Решение: 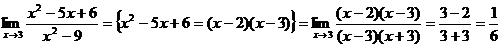
Пределы с неопределенностью вида  и метод их решения
и метод их решения
Рассмотрим группу пределов, когда 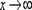 , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример. Найти предел: 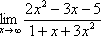
Решение: Согласно нашему правилу попытаемся подставить бесконечность¥ в функцию на место неизвестных, т.е. вместо всех х.Получим неопределенность вида  . Для раскрытия неопределенностей такого типа необходимо в числителе и знаменателе разделить многочлены на х старшей степени, т.е.
. Для раскрытия неопределенностей такого типа необходимо в числителе и знаменателе разделить многочлены на х старшей степени, т.е.
Сначала мы смотрим на числитель и находимхв старшей степени: 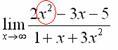 Старшая степень в числителе равна 2.
Старшая степень в числителе равна 2.
Теперь смотрим на знаменатель и тоже находим х в старшей степени: 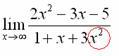 Старшая степень знаменателя равна 2.Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Старшая степень знаменателя равна 2.Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий:для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на х в старшей степени. Разделим числитель и знаменатель нах2:
необходимо разделить числитель и знаменатель на х в старшей степени. Разделим числитель и знаменатель нах2:
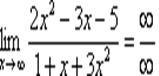
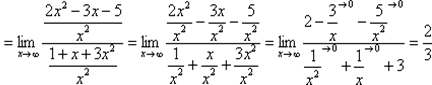
Для пределов такого вида запишем общее правило:
Общий вид предела 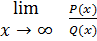
где Р(х) = а0хn + a1xn-1