Собственные векторы и собственные значения матриц и их свойства. Характеристическое уравнение и многочлен матрицы. Приведение матрицы к диагональному виду.
281. Собственные векторы и собственные значения матриц и их свойства.
Пусть 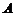 – линейный оператор в
– линейный оператор в 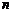 -мерном линейном пространстве
-мерном линейном пространстве 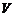 , определяемый матрицей
, определяемый матрицей 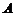 порядка
порядка 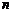 .
.
Собственным вектором данного линейного оператора (матрицы 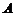 ) называется такой ненулевой вектор
) называется такой ненулевой вектор 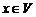 , который удовлетворяет
, который удовлетворяет
условию
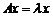 , (1)
, (1)
причем 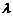 – действительное число, называемое собственным числом или собственным значением оператора
– действительное число, называемое собственным числом или собственным значением оператора 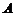 (матрицы
(матрицы 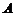 ), а
), а 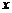 называется собственным вектором.
называется собственным вектором.
Утверждение 1. Собственные векторы и собственные значения удовлетворяют следующим свойствам:
1)Собственный вектор линейного оператора имеет единственное собственное значение 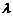 .
.
2)Если 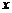 – собственный вектор линейного оператора
– собственный вектор линейного оператора 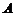 с собственным значением
с собственным значением 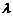 и
и 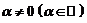 , то
, то 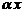 – также собственный вектор оператора
– также собственный вектор оператора 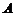 с собственным значением
с собственным значением 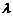 .
.
3)Если 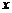 и
и 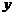 – линейно независимые собственные векторы линейного оператора
– линейно независимые собственные векторы линейного оператора 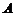 с одним и тем же собственным значением
с одним и тем же собственным значением 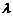 , то
, то 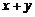 – также собственный вектор этого оператора с собственным значением
– также собственный вектор этого оператора с собственным значением 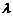 .
.
4)Если 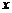 и
и 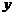 – собственные векторы линейного оператора
– собственные векторы линейного оператора 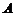 с различными собственными числами
с различными собственными числами 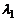 и
и 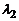 (
( 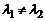 ), то
), то 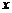 и
и 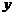 – линейно независимы.
– линейно независимы.
Преобразуем уравнение (1), определяющее собственные векторы и собственные числа линейного оператора А, к однородному уравнению.
Из (1) имеем 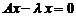 . Поскольку
. Поскольку 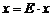 , то отсюда получаем
, то отсюда получаем 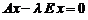 или
или
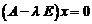 . (1’)
. (1’)
282. Характеристическое уравнение и многочлен матрицы.
Условие при котором система (1’) имеет нетривиальное решение, запишется в виде:
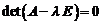 . (2)
. (2)
Уравнение (2) называется характеристическим уравнением матрицы А, многочлен 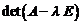 – характеристическим многочленом матрицы А, а его корни – характеристическими числами или собственными значениями матрицы А.
– характеристическим многочленом матрицы А, а его корни – характеристическими числами или собственными значениями матрицы А.
Совокупность всех характеристических чисел матрицы А называется ее спектром, причем каждое характеристическое число входит в спектр столько раз, какова его кратность в уравнении (2).
Если характеристическое уравнение (2) имеет лишь простые корни, то спектр матрицы А называется простым.
283. Приведение матрицы к диагональному виду.
Рассмотрим линейное преобразование линейного пространства V с матрицей А.
Утверждение 1. Матрица А линейного преобразования имеет диагональный вид тогда и только тогда, когда каждый базисный вектор является собственным вектором этой матрицы.
Матрица А называется приводимой к диагональному виду, если существует такая невырожденная матрица Т, что матрица 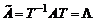 .
.
Матрица Т составляется из собственных векторов матрицы А,записанных по столбцам.
Теорема 1. Матрица А линейного оператора n-мерного линейного пространства приводима к диагональному виду тогда и только тогда, когда существует базис В этого пространства, состоящий из собственных векторов матрицы А.
Очевидно, что для построения матрицы Т достаточно найти собственные векторы матрицы А.
