Решение систем линейных уравнений методом крамера

1)вычисляетсяя опр. Системы. Это опредетельсоств. с коэффицентом при неизвестном

2)вычисл. Определители системы. Вычислопр при неизвестном, кот. Получается из опр. Системы заменой столбца коэф. При этом неизвестном столбцом.

3)х=∆х1\∆

Следствия:

1)если опр. Не равен 0, то система имеет решение, притом единственное(∆не=0)

2)если опр. Сиситемы равен 0, хотя бы один из опр. При неизвест. Равен 0, система несовместна, т.е решений нет

3) если опр. Системы равен 0, и опр. Равен 0,то система имет бесчисленное множество решений

Векторы и линейные операции над ними

Линейные операции

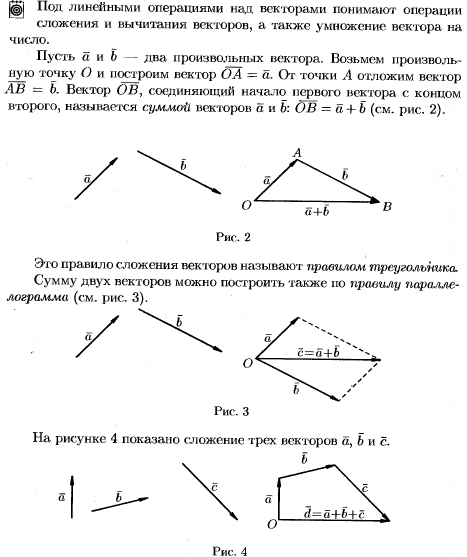
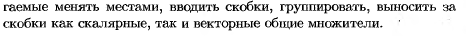
Линейная зависимость векторов

Сиситема векторов Аm называется линейно-зависимой, если один из векторов может быть представлен в виде лин. Комб.

Аn=ƛa1+ƛa2+…+ƛn-1an-1

Если усл.лин.комб. невозможно, то системы векторов наз. Линейно-независимыми

Теорема 1 любые три вектора н плоскости явл. Линейно-зависимыми

Макс.числолин. Независимых векторов на плоск. =2. Условие лин.независимости двух векторов явл.услнеколлианир.

Лин.независимые вектора состав.базис пространства. Число линейно-зависимых векторов опр. Размеренность пространства

9) базис. Декартовый базис

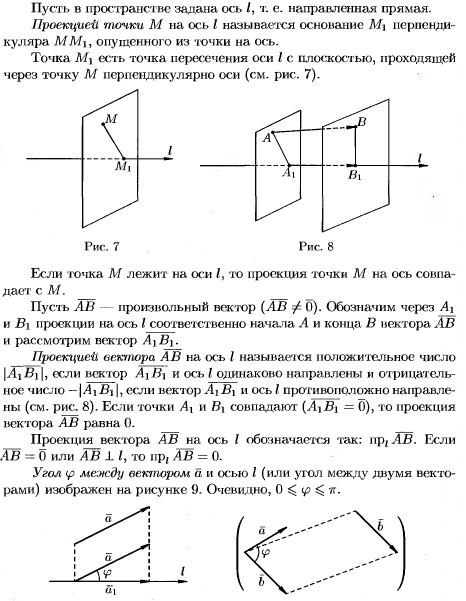
10)проекция вектора на ось

Скалярное произведение векторов и его свойства

Векторное произведение векторов и его свойства

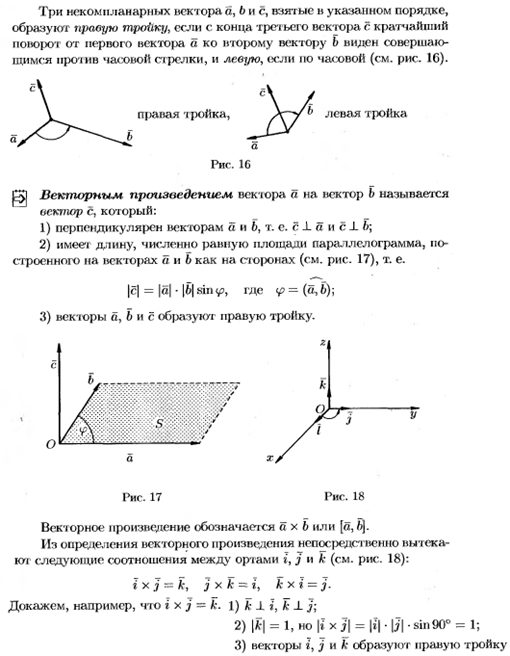
Свойства

Смешанное произведеиеветоров и его свойства

Свойства

14)общее уравнение прямой линии и его исследование

Уравнение прямой с угловым коэффицентом

16)угол м\у двумя прямыми. Условия параллельности и перпендикулярности двух прямых

Расстояние от точки до прямой

Вывод уравнения эллипса. Эксцентриситет эллипса

Гипербола и ее каноническое уравнение

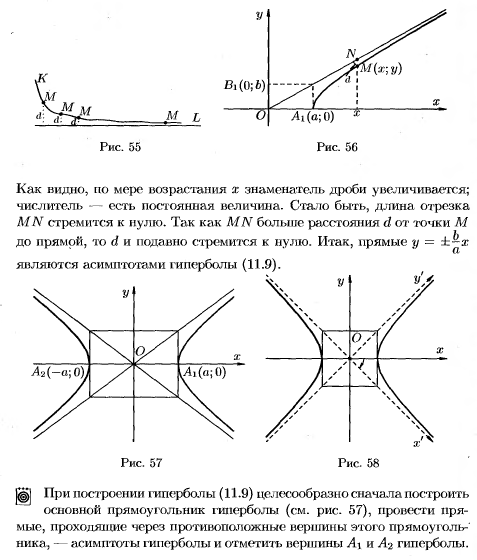
Парабола и вывод ее уравнения

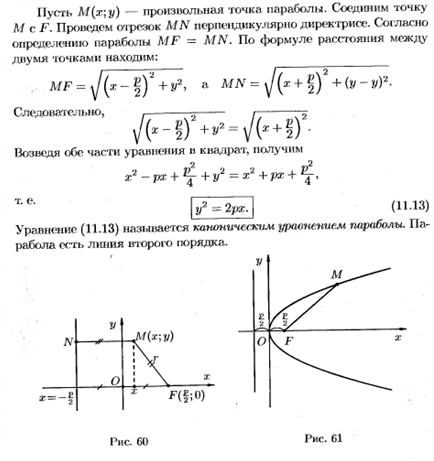
А

21)полярная система координат. Преобразование координат

Понятие об уравнении поверхности. Общее уравнение плоскости и его исследование

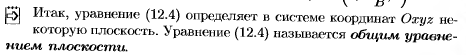
Взаимное расположение плоскостей

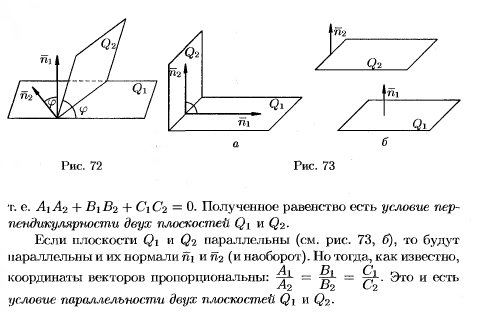
Расстояние от точки до плоскости

Прямая в пространстве. Параметрическое и каноническое уравнение прямой в пространстве

Общим уравнение прямой в пространстве явл. Прямая заданная как(прямая) линия пересечения двух плоскостей

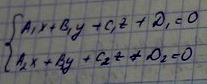
Ур-ие прямой, проходящее через данную точку ||напр.вектору

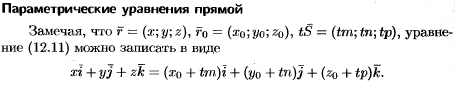
Взаимное расположение прямой и плоскости

27)понятие окрестности точи открытые и замкнутые

28)числовая функция как отображение. Способы задания функции

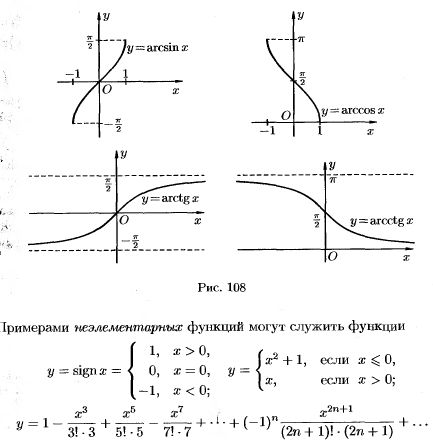
Обратные тригонометрические функции и их графики

Предел переменной величины

Постоянное числоа называется пределом переменной величины х, если для каждого наперед заданного произвольно малого положительного числа е можно указать такое значение переменной х, что все последующие значения переменной будут удовлетворять неравенству

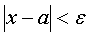
Если число есть предел переменной величины х, то говорят, что х стремится к пределу , и пишут:

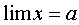
В терминах геометрических определение предела может быть сформулировано следующим образом:

Постоянное числоа есть предел переменной, если для любой наперед заданной как угодно малой окрестности с центром в точкеа и радиусом е найдется такое значение х, что все точки, соответствующие последующим значениям переменной, будут находиться в этой окрестности.