Тема: Решение систем линейных алгебраических уравнений методом Крамера

Цель работы:научиться вычислять корни систем линейных алгебраических уравнений методом Крамера.

Задание:

Решить систему линейных алгебраических уравнений с помощью формул Крамера.

1.	4x1 + 0,24x2 – 0,08x3 = 8; 0,09x1 +3x2 – 0,15x3 = 9; 0,04x1 – 0,08x2 + 4x3 = 20.	2.	2x1 – x2 + x3 = -3; 3x1 + 5x2 – 2x3 = 1; x1 – 4x2 + 10x3 = 0.
3.	10x1 +2x2 + x3 = 35; x1 + 5x2 + x3 = 29; 2x1 + 0,5x2 + 4x3 = 34.	4.	5x1 + x2 + 2x3 = 17; 2x1 + 7x2 – x3 = -7; x1 – 2x2 + 8x3 = 36.
5.	4x1 + x2 + x3 = 24; x1 + 3x2 + 2x3 = – 10; 2x1 + x2 + 7x3 = -28.	6.	5x1 + 2x2 x3 = 19; x1 + 4x2 + 2x3 = 11; 2x1 + 3x2 + 6x3 = 21.
7.	7x1 + 5x2 + 2x3 = 48; 2x1 + 10x2 – x3 = 27; x1 + 2x2 – 3x3 = 18.	8.	2x1 + 0,5x2 + 0,5x3 = 12; x1 + 3x2 + x3 = -4; 3x1 + 2x2 – 8x3 = 68.
9.	10x1 + 2x2 + x3 = 32; x1 + 5x2 + x3 = 47; 2x1 + 0,5x2 + 4x3 = 30.	10.	4x1 – x2 –2x3 = 15; 3x1 + 6x2 – x3 = 19; x1 + 2x2 + 3x3 = 13.

Вопросы для допуска к выполнению лабораторной работы:

1. В чем заключается решение систем уравнений методом Крамера?

2. Для каких матриц существуют обратные матрицы?

3. Суть метода Гаусса.

4. В чем основное отличие метода Жордана-Гаусса от метода Гаусса?

5. Запишите формулы для итерационного процесса поиска решения системы ЛАУ.

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. В каких случаях возможно решение систем уравнений методом Крамера?

2. В каких случаях нельзя пользоваться формулами Крамера?

3. Укажите соотношения для вычисления корней системы линейных уравнений по методу Крамера.

4. С помощью какой функции в Матлаб можно вычислить определитель матрицы?

5. С помощью какой функции в Матлаб можно ввести матрицу?

Лабораторная работа 10

Тема: Решение систем линейных алгебраических уравнений

Цель работы:научиться вычислять корни систме линейных алгебраических уравнений в среде Матлаб.

Задание:

Решить задания к предыдущим 2-м лабораторным работам с помощью системы Матлаб.

Теоретические сведения

Формулы Крамера

Дана система n ЛАУ:

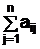x_j = b_i; (i = 1, 2, ...n). (4.1)

Образуем матрицу коэффициентов системы и векторы-колонки (векторы-столбцы) неизвестных и свободных членов:

A = [a_ij ], x = [x_j ], b = [b_i].

Матричная запись (4.1) имеет вид:

Ax = b. (4.2)

Если матрица А – неособенная (detA = D ¹ 0), то существует обратная матрица А^-1. Умножая обе части равенства (4.2) слева на обратнуюматрицу, получим

А^-1А х = А^-1 b или х = А^-1 b. (4.3)

Формула (4.3) дает решение задачи. Для вычисления корней по (4.3) нужно уметь обращать матрицы и производить их умножение.

Выражая обратную матрицу через союзную матрицу А^~ (А^-1 = А^~/ D), преобразуем (4.3) к виду:

x = 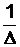A^~ b,

или x_i= D _i / D,

где D _i= 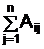A_ji b_j.

A_jI – алгебраическое дополнение элемента a_ji матрицы А.

Дополнительные детерминанты D i получаются из D путем замены i-й колонки колонкой свободных членов.

Получаем известные формулы Крамера:

x₁ = D₁ / D, x₂ = D₂ / D,... , x _n = D _n / D. (4.4)

Метод Гаусса

Пример 4.2.

Решим систему (4.5), используя метод Гаусса.

Выразим х1 из первого уравнения и подставим результат во второе и третье уравнения. Получим после простых преобразований:

2x1 + 3x2 +4x3 =15;

0 - x2/2 + 3x3 = 17/2;

0 - 13x2/2 – 5x3 = – 43/2.

Выразим из второго уравнения последней системы х2 и подставим в третье уравнение. После простых преобразований получим:

2х1 +3х2 +4х3 = 15;

0 – х2/2 +3х3 = 17/2;

0 + 0- 44x3 = – 132.

Из последнего уравнения находим х3 = 3, подставляя этот результат в предыдущее уравнение, найдем х2 =1 и из первого уравнения получим х1 = 0. Результат совпадает с (4.6).

Метод Жордана–Гаусса

Пример 4.3.

В результате описанных преобразований системе (4.5) можно придать вид:

1*x1 + 0*x2 + 0*x3 = 0;

0*x1 + 1*x2 + 0*x3 = 1;

0*x1 + 0*x2 + 1*x3 = 3;

откуда видно, что x1 = 0; x2 = 1; x3 = 3.

Метод итераций

Пример 4.4.

Рассмотрим решение следующей системы ЛАУ:

10x1 + x2 + 2x3 = 7;

x1 + 5x2 +x3 = 8; (4.8)

3x1 – 2x2 +6x3 = 16.

Преобразуем ее к виду:

x1 = 0,7 – 0,1x2 – 0,2x3;

x2 = 1,6 – 0,2x1 – 0,2x2; (4.9)

x3 = 2,67 – 0,5x1 + 0,33x2.

За нулевое приближение корней примем значения:

x1⁽⁰⁾ = 0,7; x2⁽⁰⁾ = 1,6; x3⁽⁰⁾ = 2,67.

Рассчитываем первое приближение для корней, используя в (4.9) предыдущее приближение:

x1⁽¹⁾ = 0,7 – 0,1*1,6 – 0,2*2,67 = 0,006;

x2⁽¹⁾ = 1,6 – 0,2*0,7 -0,2*1,6 = 1,264;

x3⁽¹⁾ = 2,67 – 0,5*0,7 + 0,33*2,67 = 3,20.

Второе и последующие приближения рассчитываются аналогично. Уже первое приближение дает результаты, близкие к точным значениям корней.

Вопросы для допуска к выполнению лабораторной работы:

1. В чем заключается решение систем уравнений методом Крамера?

2. Для каких матриц существуют обратные матрицы?

3. Суть метода Гаусса.

4. В чем основное отличие метода Жордана-Гаусса от метода Гаусса?

5. Запишите формулы для итерационного процесса поиска решения системы ЛАУ.

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. Что значит решить СЛАУ?

2. Какой метод решения СЛАУ Вы выбрали?

3. Почему был выбран именно этот метод решения СЛАУ?

4. В чем основное отличие метода Жордана-Гаусса от метода Гаусса?

5. Запишите формулы для итерационного процесса поиска решения системы Вашей СЛАУ.

Лабораторная работа 11