Конечные и бесконечные множества.
Непустое множество называетсяконечным,если число его элементов выражается целым положительным числом.
Мн-ва могут содержать как конечное число элементов, так и бесконечное.
Например: мн-во цветов в вазе –конечно, мн-во точек прямой – бесконечно.
9. Диаграммы Эйлера и их применение. Способы задания множеств. Понятие подмножества. Основные свойства отношения включения. Число подмножеств конечного множества.
Множество – это одно из основных неопределяемых понятий в современной математике.
Множества обозначаются заглавными латинскими буквами: M, A, B, C и т.д.
Объекты, которые принадлежат мн., называются его элементами. Если элементы множеств буквы, то их обозначают маленькими лат.буквами: a, b, c и т.д.
Если элемент принадлежит множеству, то обозначается так: a ϵ A «a является элементом множества A»
Если нет, то:b не принадлежит (значок) A.
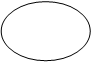 |
это круг Эйлера(диаграмма Эйлера)
∙ a ∙ b
A
aявл. элементом A.
Любой элемент в A может содержаться только 1 раз (не более).
Синонимы: коллекция, совокупность, набор, группа и т.д.
Множество может
Способы задания множества:
Множество можно задать разными способами. При каждом из этих способов множества записываются по-разному.
Перечислением его элементов
Например: мн. A = {b,c,d} задано точным перечислением всех его элементов (так можно задать лишь конечное множество)
Указанием характеристического свойства элементов
Например: Нельзя перечислить все натуральные числа (это бесконечное множество).
Характеристическое свойство множества – множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты.
Например: мн. всех простых чисел N. Этому мн. принадлежат те и только те натуральные числа больше 1, которые делятся на 1 и сами на себя.
Понятие подмножества
Множество называется конечным, если все его элементы можно перечислить.
Например: множество натуральных чисел – бесконечное. Для того, чтобы удобно было представить множество, их принято обозначать кругами Эйлера (см. рисунок).
Мн. A называют частью или подмножеством другого множества B, если каждый элемент из мн. Aявл. элементом множества B.
Например: множество всех прямоугольников включается в множество параллелограммов.
Каждое пустое мн. Aимеет по крайней мере 2 подмножества: пустое мн. и само мн. A. Пустое множества считается подмножеством любого множества.
Множества могут находиться в различных отношениях:
1) множества не имеют общих элементов
A = {a,b,c} B = {m,n}
2) множества имеют некоторые общие элементы
A = {a,b,c,d} B = {m,n,a,d}
3) A подмножество множества B (все элементы мн. A принадлежат мн. B)
A = {a,b,c} B = {a,m,n,b,c,f}
4) все элементы A принадлежат B и все эл. B принадлежат A.
A = {a,b,c} B = {c,a,b}
Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.10. Основные операции над множествами: объединение, пересечение, вычитание, дополнение до универсального (УАО), симметрическое вычитание, декартого умножение. Свойства.
Вычитание множеств.
Определение:
Разностью множеств A и B называется множество A – B, состоящее из тех и только тех элементов множества A, которые не являются элементами множества B.
Например:
Для А = {1,2,3,4,5} и B = {2,4,6}
А – В = {1,3,5}
Например:
Если А – множество всех ромбов, а В – прямоугольников, то А – В = множество всех ромбов, кроме квадратов, а В – А = множество, состоящее из всех прямоугольников, которые не являются квадратами.
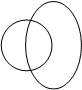 |
А В
А – В (левое ухо)
Теорема о свойствах:
Вычитание – операция для нахождения разности (БАО).
Всегда:
1о. А – Ø = А (Ø – правый нейтральный элемент)
2о. Ø – А = Ø (Ø – левый поглощающий элемент) (см. определение и рисунок)
3о. А – А = Ø
4о. А – В = А – (А пересечение В)
Доказательство:
см. определение и рисунок.
