Перечислением можно задать только конечные множества. Вторым и третьим способами задаются бесконечные множества.

ТЕОРИЯ МНОЖЕСТВ,

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА

ЛЕКЦИИ ПО МАТЕМАТИКЕ. ЧАСТЬ 1.

Ставрополь

ББК 22.1

УДК 514.2, 512.64

С 50

Печатается по решению

редакционно-издательского совета

Ставропольского государственного

университета

Смирнов А.А.

С 50Теория множеств, аналитическая геометрия и линейная алгебра: Лекции по математике. Часть 1: Учебное пособие – Ставрополь: Изд-во СГУ, 2003. – 130 с.

Учебное пособие представляет собой курс лекций, содержащий три раздела: «Теория множеств», «Аналитическая геометрия», «Линейная и векторная алгебра».

Предназначено для студентов I курса биолого-химического факультета по специальности 011600 – Биология, а может быть использовано для специальностей 013400 – Природопользование, 011000 – Химия.

Рецензенты:

кандидат физ.-мат. наук, доцент А.Н. Макоха

кандидат тех. наук, преподаватель ФРВИ РВ М.Э. Солчатов

© Издательство Ставропольского

государственного университета, 2003

Движение точки – прямая. Движение прямой – плоскость. Движение плоскости – пространство. Движение пространства – четвертое измерение.

Предисловие

Пособие составлено в соответствии с авторской программой по математике и Государственным образовательным стандартом высшего профессионального образования для студентов специальности 011600 – Биология, и представляет собою курс лекций, охватывающий три раздела: «Теория множеств», «Аналитическая геометрия», «Линейная и векторная алгебра», являющиеся составной частью курса математики. Традиционно эти разделы читаются в первом семестре.

Пособие содержит основные понятия, определения, теоремы и наиболее важные задачи. План лекции позволит студенту представить структуру всего курса и место каждого вопроса в ней. Предлагаемая литература к лекции даст возможность познакомиться с различными подходами в изучении вопросов и глубже их понять.

В курсе лекций излагаются оригинальные взгляды на некоторые вопросы математики, обобщаются многие теоретически сложные вопросы, что позволяет интегрировать аппарат высшей математики в прикладные вопросы различных специальностей. Приведены примеры из многих прикладных областей. Оригинальность некоторых рисунков упрощает восприятие сложных вопросов. Ряд теорем и формул приведены с доказательством, так как использованные в нем приемы можно применять при решении практических задач.

Вводная часть позволит студенту представить не только структуру конкретной лекции, но и ее роль, и место в курсе высшей математики. В конце лекции сделан акцент на особо важных вопросах, что закрепляет полученные знания. Причем аспекты расставлены таким образом, что заставляют задуматься над, казалось бы, известными ранее вопросами. Кроме того, по ходу лекции на наиболее важных выводах делается особый акцент.

Тот не рожден для теоретических исследований, кто в молодости не восхищался «Началами» Евклида.

А. Энштейн

Развитие математики

(краткая историческая справка)

Последние данные говорят о том, что время зарождения математики имеет срок, равный появлению человека разумного на Земле. Очевидно, как только человек стал разумным, он уже пытался отличать один предмет от двух или от множества. Однако первыми древними цивилизациями, от которых до нас дошли источники, позволяющие судить об их математических познаниях, были вавилонская и египетская цивилизации. В результате раскопок на месте вавилонской цивилизации было найдено около 300 глиняных табличек, имеющих отношение к математике и датируемых с 1900 по 1600 г. до н. э. На этих табличках встречаются ряды чисел, геометрические соотношения и задачи.

Одновременно развивалась математика Древнего Египта, первые свидетельства которой датируются временем расцвета египетской цивилизации, начиная с третьей династии фараонов (около 2500 лет до н. э.). Раскопки позволили узнать об иероглифической и иератической системах письма. Один из самых известных документов – папирус Ринда, хранящийся в Британском музее (около 1650 г. до н. э.).

Отметим вкратце этапы дальнейшего развития математики.

1. Древняя Греция. После окончания периода завоеваний индоевропейцами Средиземноморского побережья на заре XIII в. до н. э. появились первые зачатки греческой цивилизации с главным городом Милет (VI в. до н. э). О зарождении греческой математики судить сложно. К настоящему времени сохранилось только несколько фрагментов александрийских папирусов. После завоевания (334 г. до н. э.) Александром Македонским Египта (Александрии) греческая математика стала интенсивно развиваться.

В этот период жили:

великий математик Евклид (III в до н. э.), - великий труд – «Начала» (13 книг); основоположник современной математики (понятия точки линии и т.д.);

математик, механик и философ Древней Греции Аристотель (384 – 322 гг. до н. э.), - скорость звука меньше скорости света;

математик и механик Древней Греции Архимед (287 – 212 гг. до н. э.); отношение объема цилиндра к объему вписанного в него шара и объему вписанного в шар конуса составляет (3:2:1).

2. Арабская цивилизация (VII - XIII вв. н. э.). Падение Александрии (в 640 г.) ознаменовал закат греческой цивилизации. В эту эпоху начались великие завоевания территорий мусульманским миром. Образовалась огромная мусульманская империя от Индии до Испании, включая Северную Африку и южную Италию. Центром империи стал Дамаск (Сирия). Начался расцвет арабской науки.

Любой труд, чтобы получить вес в науке, должен был быть написан на арабском языке. В силу богатства языка многие математические понятия получили новое толкование. В течение 8 веков арабы стали хранителями мудрости и просветителями. Их достижение – десятичная система счисления с нулем.

В этот период жили:

арабский математик Аль-Хорезми Абу Абдаллах (около 800 – 847 гг. н. э.), - теория квадратных уравнений; теория десятичной системы;

математик и астроном Аль-Каши ( - 1429 г. н. э.), - «Ключ к арифметике», «Трактат об окружности» и др.

Арабская цивилизация стала мостом и хранителем древних знаний, переданных после европейцам.

3. Век великих переводов. Эпоха христианского средневековья продлилась с 476 г. – падение Римской империи – и по 1453 г. взятие турками Константинополя. Она сопровождалась упадком цивилизации и науки. Начиная с XII в. европейцам был открыт доступ к арабской науке. Барьером на ее пути являлся арабский язык. Поэтому XII век стал веком великих переводов.

В этот период жили:

математик и философ Леонардо Пизанский (Фибоначчи) (1170 – 1250 гг. н. э.), - числа Фибоначчи;

итальянский математик, механик и художник Леонардо да Винчи (1452 – 1519 гг.), - один из основоположников правил перспективы.

4. Математизация науки в XVII в. Открытия Коперника и Кеплера способствовали впоследствии бурному развитию математики. Они показали, что явления природы подчиняются точным математическим законам.

В этот период и позже жили:

французский философ, физик, математик Рене Декарт (1596 – 1650), - система координат;

английский физик, механик, астроном и математик Исаак Ньютон (1642 – 1727);

немецкий философ и математик Генрих Лейбниц (1646 – 1716);

математик, механик и физик Леонард Эйлер (1707 – 1783);

кроме того, перечислим наиболее значимые события.

Ферма – Теория чисел, Виет – совершенствование алгебры, Паскаль и Ферма – создание теории вероятностей, Лейбниц и Ньютон – исчисление бесконечно малых. Началась эпоха академий наук. Появились такие ученые-математики, как Лагранж, Ламберт, Бернулли, Даламбер и др.

5. Эпоха расцвета французской математики. Это было время Французской революции, в которой принимали участие и великие математики. В 1794 г. была основана Политехническая школа. В ней преподавали Монж, Лагранж, Ампер, Пуассон, Фурье, Коши и др. Франция как центр науки привлекала к себе многих ученых. В конце этой эпохи жил французский математик Огюстен-Луи Коши (1789 – 1857).

6. Современная эпоха математики. Начиная с XIX в. больше стало возможностей в общении ученых. Стало больше публикаций и росло количество теоретических результатов. Этому способствовало развитие технического прогресса, демократизации и капитализации общества. Стало больше научных центров: Норвегия – Абель, Венгрия – Бойяи, Чехословакия – Больцано и др. Германия становится одним из научных центров.

Немецкий математик К. Ф. Гаусс (1777 – 1855) – «король» математики. Его постулат: «Профессор может обучать всему, чему пожелает».

В Кенигсберге работал Якоби, в Берлине – Дирихле (с 1844 по 1855 гг.), в Геттингене – Риман (с 1854 по 1866 гг.). Далее там работал Гильберт. Славилась и вторая Берлинская школа, возглавляемая с 1860 г. Куммером, Кронекером, Вейерштрассом.

Стали появляться первые математические школы: Лондонское математическое общество (1865), Московское математическое общество (1866), Французское математическое общество (1872), Американское математическое общество(1888), Немецкое математическое общество (1890).

В России в этот период тоже появились великие ученые. Выдающийся математик, академик М.В. Остроградский (1801 – 1862) – основатель петербургской математической школы, Н. И. Лобачевский (1792 – 1856) – создатель неэвклидовой геометрии, П.Л. Чебышев (1821 – 1894) – теория чисел, теория вероятностей и приближений, А.А. Марков (1856 – 1922) – теория случайных процессов, А.М. Ляпунов (1857 – 1918) – теория устойчивости движения, Е. И. Золотарев и др.

Важный вклад в математику сделали советские ученые: А. Д. Александров, П. С. Александров, С. Н. Бернштейн, Н. Н. Боголюбов, И. М. Виноградов, В. М. Глушков, Л. В. Канторович, М. В. Келдыш, А. Н. Колмогоров, Ю. В. Линник, А. И. Мальцев, П. С. Новиков, Л. С. Понтрягин, С. Л. Соболев, А. Н. Тихонов. Благодаря им наша страна выведена на одно из первых мест в мире по развитию математики.

В настоящее время все большую роль начинает играть прикладная математика. Применение математики в таких науках как биология, астрономия, химия и др. открывает новые горизонты не только в решении технических задач, но развивает саму математику. Что стоит открытие генома человека, клонирование, создание нейрокомпьютеров и др. О таких достижениях без применения современной математики нельзя было и мечтать. Этот процесс непрерывен, он продолжается и будет все более охватывать сознание прогрессивного человечества.

В 1890 году Гильберт изложил перед Вторым международным конгрессом список из 23 проблем, которые должны определять ход будущей математики XX в. Многие проблемы до сих пор не решены.

Математика – это тот точный «инструмент», которым пользуются практически все науки для осознания, описания или даже предсказания окружающего нас мира, включая человека как субъекта. С того момента как человек осознал, что два предмета это больше одного ему уже понадобился математический аппарат. Он зарождался в подсознании и помогал развиваться человечеству. Математика это то звено, которое объединяет все науки и позволяет им называться науками.

Лекция 1

Теория множеств

Основные понятия теории множеств

Подмножество

Свойства включений

Цели занятия: изучить основные понятия дискретной математики, научиться рассматривать окружающую природу и события через множества; познакомиться с основными отношениями множеств.

Роль и место лекции

Этой лекцией мы начинаем изучение высшей математики. Неслучайно оно изучение начинается с теории множеств. С этой теории должно начинаться знакомство с математикой вообще. Мы должны определиться, с какими элементами будем оперировать. Дискретная математика стоит на стыке строгих теорий и логических умозаключений, т. е. зачастую позволяет осмыслить строгие математические выражения. Например, в школьном курсе математики было дано понятие функции как зависимости ее значений y от некоторой переменной x. С точки зрения высшей математики функция – это некоторое отношение между множествами, элементами которых, в частности, могут быть и упомянутые переменные, а также люди, звезды и т. д.

Основные понятия теории множеств

Большую часть понятий дискретной математики можно определить с помощью понятия множества. Множество - основополагающее, первичное и неопределяемое понятие математики. Множеством принято называть набор, совокупность некоторых объектов, при этом природа самих объектов, составляющих то или иное множество, не имеет значения. Создатель теории множеств Георг Кантор давал следующее определение множества – "множество есть многое, мыслимое нами как целое".

Понятие множества

Определение 1.

Объекты, из которых состоит то или иное множество, называют элементами этого множества. В математике употребляются следующие синонимы термина множество: система, класс, совокупность.

Как уже говорилось, множества могут быть самой различной природы, например, множество всех деревьев в городе на сегодняшний день. В качестве другого примера множества можно принять следующее определение: множество всех студентов, сидящих сейчас в соседней аудитории. В первом примере элементами множества являются деревья, а во втором – студенты.

В математике рассматриваются более специфические множества, состоящие из чисел, кривых, множеств чисел и т.д.

Замечание!!!

Множества принято обозначать прописными буквами латинского алфавита, а их элементы – строчными буквами с индексом или без него.

Например, множества A, B, ... X, Y, Z и соответственно элементы a, b,... x, y, z. С целью упрощения многих математических записей и придания им наглядности в математике помимо стандартных кванторов общности и существования вводят так называемые сокращения высказывания, например, знакомые вам “>”, “ 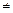” и т. д. Запишем основные сокращения, используемые в высшей математике.

Сокращения

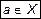– "элемент a принадлежит множеству X ";

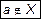– "элемент a не принадлежит множеству X ";

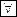– обозначение произвольности, читается " 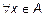- для любого элемента x множества A";

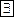– обозначение существования, читается " 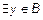- существует (найдется) элемент y из множества B";

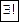– обозначение существования и единственности, " 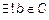существует единственный элемент b из множества C";

: – “такой, что” или “обладающий свойством”. Обычно таким значком дополняется предыдущее сокращение .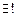

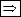– обозначение следования - "если ..., то ...";

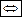– обозначение равносильности - "тогда и только тогда".

Множества могут быть заданы тремя основными способами.

Способы задания множеств

1)Перечислением. Множество можно задать, перечислив все его элементы. Обозначение списка записывается в фигурных скобках.

ПРИМЕР 1.

А={январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь} – множество месяцев года.

2) Порождающей процедурой. Трудно перечислить все натуральные числа от 2 до 2ⁿ. В этом случае множество задается описанием способа получения его элементов. Элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры.

ПРИМЕР 2.

Множество всех чисел, являющихся степенями двойк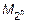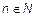и , или 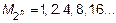, может быть задано порождающей рекурсивной или индуктивной процедурой:

а) 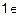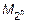или б) если 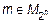, то .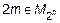

3) Описанием характеристических свойств. Множество можно задать при помощи объявления свойства, определяющего, какие элементы принадлежат, а какие не принадлежат описываемому множеству. В этом случае множество задается в фигурных скобках записью общего элемента и свойства всех элементов.

ПРИМЕР 3.

Множество в предыдущем примере .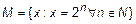

Наиболее часто используемые виды множеств:

A – некоторое множество физических объектов, цен, услуг и т. д.;

N – множество натуральных чисел N= {1, 2, 3,... };

Z – множество целых чисел Z= {0, ±1, ±2, ±3,... };

Q – множество рациональных чисел Q= { : , };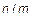

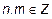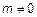R – множество действительных (вещественных) чисел.

Множество может содержать много элементов или лишь несколько, например множество русских букв содержит ровно 33 элемента. Множество натуральных чисел N содержит бесконечно много элементов. Может быть и предельный случай, когда множество вообще не содержит элементов, например множество действительных корней уравнения x⁴+8 = 0.

Определение 2.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается .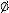

В общем случае множества бывают конечные и бесконечные.

Определение 3.

Конечное множество – это такое множество, для которого существует натуральное число, равное числу его элементов.

Например, множество русских букв – конечное множество, так как существует натуральное число 33, равное числу элементов этого множества.

Определение 4.

Множество, не являющееся конечным, называется бесконечным множеством.

Замечание!!!

Перечислением можно задать только конечные множества. Вторым и третьим способами задаются бесконечные множества.

Уже рассмотренное нами множество натуральных чисел N – бесконечное множество, поскольку нет такого натурального числа, которое равнялось бы числу его элементов.

Определение 5.

Если множество A – конечное множество, то через |A| обозначают число его элементов и называют мощностью множества A. Понятие мощности вводится и для бесконечных множеств.

ПРИМЕР 4.

Пусть множество A состоит из элементов {январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь} – это множество месяцев одного года. Мощность |A| заданного таким образом множества A равна 12. Это число элементов множества A – количество месяцев одного года.

Определение 6.

Два конечных множества A и B называются равными, если они состоят из одних и тех же элементов. Если множества A и B равны, то мы будем писать A = B, в противном случае A 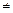B.

Вывод!!!

В равных множествах последовательность элементов не важна. Таким образом, мы получили следующее определение:

Определение 7.

Два конечных множества A и B не равны между собой, если в множестве A есть элемент, не принадлежащий множеству B или наоборот.

Вывод!!!

Согласно такому определению равенства множеств мы, естественно, получаем, что все пустые множества равны между собой или (что то же самое) что существует только одно пустое множество .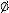

ПРИМЕР 5.

1. Множества {0, 1, 2}={1, 2, 0} равны между собой и поэтому между ними мы можем поставить знак равенства: они конечны и состоят из одних и тех же элементов.

2. Рассмотрим теперь три множества A={0,1}, B={{0,1},2} и C={{{0,1},2},3}. Между этими множествами справедливы следующие соотношения .

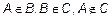Важно!!!