О представлении действительных чисел.

Мы видели, что формирование числовых систем при помощи аксиоматик натуральных, рациональных и действительных чисел связано с выполнением следующих интеллектуальных функций: перечисление объектов (операция счёта), арифметические операции над натуральными числами и, наконец, измерение длин геометрических протяжённостей. Для реализации этих операций надо построить символьную систему, в которой станет возможным выполнение указанных функций нашего интеллекта. Таким образом, наша цель – решение следующей задачи.

Задача 3.

Построить символьную запись действительных чисел, в которой: а) допустимо измерение длины любого отрезка, б) реализуются арифметические операции над действительными числами.

Мы покажем, что запись действительных чисел в десятичной системе является подходящей для этой цели.

Нам потребуется понятие взаимно-однозначного соответствия множеств.

Определение взаимно-однозначного соответствия. Будем говорить, что между элементами хмножества Х и элементами у множества У установлено взаимно-однозначное соответствие у= f(x), если каждому хиз Х соответствует единственный у из У и наоборот, для каждого у из У существует единственный х из Хтакой, что у= f(x).

Для решения задачи а) достаточно установить, что между точками прямой и действительными числами в десятичной записи существует взаимно-однозначное соответствие. Для простоты ограничимся записью чисел x Í [0,1]. Пусть точка М –произвольная точка единичного отрезка прямой. Разобьём этот отрезок на 10 равных частей и пронумеруем эти отрезки цифрами 0, 1, 2, …,9, разместив их с левой стороны отрезков, рис 1.3

0 М 1

0 1 2 … … 8 9

Рис. 1.3.

Если точка М попала в отрезок под номером где одно из чисел0,1,2, 3, …, 9, то этой точке на данном этапе построения сопоставим число х= 0, и разделим этот -отрезок снова на десять равных частей, рис. 1.4. Точка М окажется в каком-то отрезке под номером ,лежащем в предыдущем отрезке, и мы напишем х= 0, ,

a1 М a1+1

0 1 2 … … 8 9

Рис. 1.4.

Продолжая этот процесс, мы можем оказаться в одной из следующих трёх ситуаций.

1) На n-ном этапе этого процесса точка М совпадёт с риской, разделяющей два смежных отрезка. Выберем для нумерации левый отрезок и закончим процесс построения координаты точки М. В этом случае точке М будет соответствовать координата

х = 0, … ,

имеющая конечную десятичную запись и являющаяся рациональным числом.

2) Точка М никогда не совпадёт с риской деления, процесс построения приведёт к бесконечной десятичной записи, в которой с некоторого места возникают периодические блоки вида … . В этом случае точке М ставится в соответствие координата в виде бесконечной периодической десятичной дроби (для простоты мы выписали случай, когда блоки стали повторяться с самого начала)

х = 0, … … … … …

Как мы видели при построении рациональных чисел в п.1.2, эта запись так же представляет рациональное число.

3) Процесс построения приведёт к бесконечной непериодической десятичной записи, в которой нет повторяющихся блоков. Десятичной записью координаты точки М будет запись

х = 0, … …

которую назовём бесконечной непериодической десятичной дробью. В этом случае число х является иррациональным.

Таким образом, мы исчерпали все возможные появления десятичного адреса заданной точки М. Теперь надо проверить, что бесконечная десятичная запись определяет некоторое число. Для периодических дробей мы этот факт установили. Для непериодических дробей существование числа следует из оценки

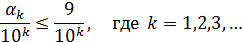
Применяя эту оценку, получим

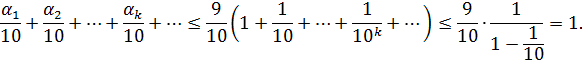
Таким образом, запись вида х = 0, … определяет число, меньшее единицы.

Замечание 2. В построении координат точки М мы воспользовались следующим свойством прямой. Последовательность вложенных друг в друга отрезков прямой при условии уменьшения их длин (на k-том шаге нашего процесса длина промежутка равна 1/10^k) стягиваются к точке и эта точка единственна. Такое свойство прямой мы увидим при формировании аксиоматики геометрии Евклида в следующем параграфе.

Итак, для произвольной точки единичного отрезка мы построили её числовое значение в виде конечной или бесконечной десятичной записи.

Теперь решим обратную задачу. Покажем, что каждой из возможных записей действительного числа в десятичной системе соответствует некоторая точка М на прямой. Для этого десятичную запись рассмотрим как адрес этой точки на прямой. Первый знак в десятичной записи х = 0, … укажет положение точки М с точностью до 1/10, два знака ,определят точкуМ с точностью до 1/100, и так далее. Запись х = 0, … с nзнаками после запятой определят точку М с точностью до 10^-n. Если десятичная дробь конечна, то мы получим точное положение точки М. Если десятичная запись бесконечна, то процесс сужения промежутка нахождения точки теоретически может продолжаться до как угодно малого промежутка. Тогда согласно аксиоме Кантора (16-той в списке аксиом действительных чисел) найдётся общий элемент для всех промежутков и этот элемент является действительным числом.

Теперь обратимся к решению задачи б) о реализации арифметических операций над числами в десятичной записи. Если число является рациональным и имеет конечную десятичную запись, то все арифметические операции выполняются по правилу действия «столбиком» известным из школьного курса. Если число записывается бесконечной дробью, то в случае рационального числа можно вернуться к записи и проделать с ним арифметические операции. Если число иррациональное или рациональное с очень большим периодом, то оно заменяется близким рациональным числом с конечной десятичной записью и над ним совершаются операции по правилу «столбика». Какова будет потеря точности вычислений при замене бесконечной десятичной дроби конечной её частью? Рассмотрим десятичные приближения. Пусть m/n = a₀, a₁…a_k – десятичное приближение с k знаками после запятой числа a = a₀,a₁…a_ka_k+1… . Тогда погрешность этого приближения определяется разностью:

| a – m/n | = a_k+1/10^k+1 + a_k+2/10^k+2 + … < 9/10^k+1(1 + 1/10 +…) =

= 9/10 ^k+1´1/(1–1/10) = 1/10^k

Любые практические измерения и вычисления имеют разумный предел точности, который устанавливается, исходя из реальных потребностей. Поэтому, выбирая достаточно хорошее приближение числа с длинной десятичной записью числом с разумно короткой десятичной записью, мы реализуем арифметические операции с необходимой точностью.

Замечание 3.

Можно поставить следующую задачу: построить такое представление действительных чисел, в котором иррациональные числа приближаются рациональными числами наилучшим образом. Рациональная дробь p/q приближает иррациональное число a наилучшим образом, если для любого рационального числа m/n с n£q выполняется равенство |a–p/q| < |a–m/n|.

Для приближений лучших, чем десятичные приближения используются представление числа цепной дробью, [6]. Если p/q - конечная цепная дробь, приближающая число a, то [2], стр. 46, |a–p/q| < 1/q².

Таким образом, представление числа цепной дробью «более экономично», чем представление десятичной дробью.

Эффективные алгоритмы арифметических операций для представлений чисел в виде цепных дробей до сих пор не найдены, [2], стр. 29-30.