Отрезок. Длина отрезка. Треугольник. Правила
Натуральные числа. Правила
| Для счёта предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: О, 1, 2, 3, 4, 5, 6, 7, 8, 9. Например: триста двадцать восемь - 328 пятьдесят тысяч четыреста двадцать один - 50421 Такую запись чисел называют десятичной. |
| Последовательность всех натуральных чисел называют натуральным рядом: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ... |
| Самое маленькое натуральное число — единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нем нет. |
| Значение цифры зависит от ее места в записи числа. Например 375: цифра 5 означает: 5 единиц, она на последнем месте в записи числа (в разряде единиц), цифра 7 - десятки, она находится на предпоследнем месте (в разряде десятков), цифра 3 - сотни, она стоит на третьем месте от конца (в разряде сотен) и т. д. |
| Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа "нуль". Это число означает "ни одного". Помните! Нуль не относят к натуральным числам. |
| Если запись натурального числа состоит из одного знака — одной цифры, то его называют однозначным. Например, числа 1, 5, 8 — однозначные. Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным. числа 14, 33, 28, 95 — двузначные, числа 386, 555, 951 — трехзначные, числа 1346, 5787, 9999 — четырехзначные и т. д. |
Плоскость. Прямая. Луч. Правила
| Примеры плоскостей мы встречаем в жизни постоянно. Это поверхности окна, парты, школьной доски, но в отличие от этих поверхностей математическая плоскость не ограничена краями. Она простирается бесконечно во все стороны. |
 Нарисуем две точки A и B . Проведем через них по линейке линию как на рисунке. У нас получилась прямая, которую обозначают прямая AB или прямая BA . Через любые две точки проходит одна единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки A и B лежат на прямой. Прямая разделяет плоскость на две части, две полуплоскости. Нарисуем две точки A и B . Проведем через них по линейке линию как на рисунке. У нас получилась прямая, которую обозначают прямая AB или прямая BA . Через любые две точки проходит одна единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки A и B лежат на прямой. Прямая разделяет плоскость на две части, две полуплоскости. |
 Если прямую AB разделить точкой O, то мы получим два луча, которые будут называться луч OB и луч OA . Переставлять буквы в их названиях нельзя, потому что точка O является началом этих лучей, и названия начинаются именно с нее. В отличие от прямой луч бесконечен только в одну сторону. Если прямую AB разделить точкой O, то мы получим два луча, которые будут называться луч OB и луч OA . Переставлять буквы в их названиях нельзя, потому что точка O является началом этих лучей, и названия начинаются именно с нее. В отличие от прямой луч бесконечен только в одну сторону. |
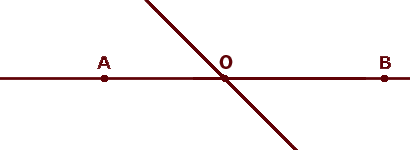 Если две прямые имеют общую точку, например O , как на рисунке, то говорят, что они пересекаются в этой точке. Точка O — точка пересечения прямых. Если две прямые имеют общую точку, например O , как на рисунке, то говорят, что они пересекаются в этой точке. Точка O — точка пересечения прямых. |
Шкалы и координаты. Правила
  Длины измеряют разными измерительными приборами. Один из них — линейка (рис. сверху). Деления, нанесенные на линейку, разбивают ее на равные части. Расстояние между мелкими рисками равно 1 миллиметр, а между крупными 1 сантиметр. Шкалы могут быть и на других измерительных приборах, например термометр (рис. слева). Данный термометр имеет цену деления равную 1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).Наведите курсор на рисунок и подождите. Длины измеряют разными измерительными приборами. Один из них — линейка (рис. сверху). Деления, нанесенные на линейку, разбивают ее на равные части. Расстояние между мелкими рисками равно 1 миллиметр, а между крупными 1 сантиметр. Шкалы могут быть и на других измерительных приборах, например термометр (рис. слева). Данный термометр имеет цену деления равную 1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).Наведите курсор на рисунок и подождите. |
На рисунке внизу изображен луч ОХ. Отметим на этом луче точку F . Под началом луча, точка O , напишем число 0 , а под точкой F — число 1. Отрезок OF называется единичным отрезком. Нанесем на луч точку D , так чтобы расстояние OF было равно расстоянию FD и под точкой D напишем число 2 . Затем на этом же луче отложим отрезок DE , равный единичному отрезку, и под точкой E напишем число 3 . Повторяя эти действия, мы получим бесконечную шкалу. Ее называют координатным лучом. Числа 0, 1, 2, 3, ... , соответствующие точкам O, F, D, E ... , называют координатами этих точек. Пишут: О(0), F(1), D(2), E(3) и т. д.  |
 На рисунке выше изображены кухонные весы, которые используются для измерения массы. Вы видите две шкалы, наведите мышку на рисунок. На первой цена большого деления равна 500 грамм , а меньшего — 100 грамм. На втором рисунке цена большого деления 200 г. , меньшего — 100 г. , а самого маленького 25 г. По подписям делений хорошо видно что, 1000 грамм равны 1 килограмму. 1000 г = 1 кг (килограмм); 1 г = 1000 мг (миллиграмм); 100 кг = 1 ц (центнер); 1000 кг = 1 т (тонна). На рисунке выше изображены кухонные весы, которые используются для измерения массы. Вы видите две шкалы, наведите мышку на рисунок. На первой цена большого деления равна 500 грамм , а меньшего — 100 грамм. На втором рисунке цена большого деления 200 г. , меньшего — 100 г. , а самого маленького 25 г. По подписям делений хорошо видно что, 1000 грамм равны 1 килограмму. 1000 г = 1 кг (килограмм); 1 г = 1000 мг (миллиграмм); 100 кг = 1 ц (центнер); 1000 кг = 1 т (тонна). |
Сравнение чисел. Правила
При счете натуральные числа называют по порядку: 1, 2, 3, 4, ... . Число, которое при счете называют раньше, меньше того, которое при счете называют позже. Число 1 меньше, чем 3, а число 4 больше, чем 3. Единица — самое маленькое натуральное число. Точка с меньшей координатой лежит на координатном луче левее точки с большей координатой. 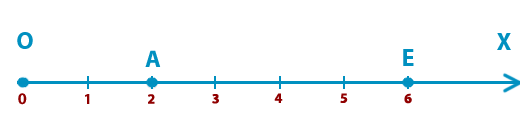 Например, точка A(2) (см. рисунок) лежит левее точки E(6). Нуль меньше любого натурального числа. Например, точка A(2) (см. рисунок) лежит левее точки E(6). Нуль меньше любого натурального числа. |
| Результат сравнения двух чисел записывают в виде неравенства, применяя знаки < (меньше) и > (больше) . Например: 1 < 3 ; 4 > 3 ; 5 < 7 . Число 3 меньше, чем 4, и больше, чем 1. Это записывают в виде двойного неравенства: 1 < 3 < 4 . Так как нуль меньше, чем единица, то записывают: 0 < 1 . |
| Многозначные числа сравнивают так. Число 1007 больше, чем 929, потому что 1007 — четырехзначное число, а 929 — трехзначное. 1007 > 929. Числа 3221 и 1723 — четырехзначные, но 3221 > 1723, потому что в первом числе больше тысяч, чем во втором. В четырехзначных числах 7505 и 7287 поровну тысяч, но сотен в первом числе больше, и потому 7505 > 7287 . |
Знаками < и > обозначают также результат сравнения отрезков.  Если отрезок OA короче отрезка AE, то пишут: OA < AE. Если отрезок OA короче отрезка AE, то пишут: OA < AE. |
 Если же отрезок OA длинее отрезка AE, то пишут: OA > AE . Если же отрезок OA длинее отрезка AE, то пишут: OA > AE . |
| Легкий способ запоминания, когда использовать < , а когда > , для сравнения чисел. Меньшее число должно находиться с острого (маленького) конца знака, а большее с широкого (большого) конца знака: 1 < 3 ; 3 > 1. |
| Сложение и вычитание натуральных чисел |
 6. Сложение натуральных чисел и его свойства 6. Сложение натуральных чисел и его свойства |
 7. Вычитание натуральных чисел и его свойства 7. Вычитание натуральных чисел и его свойства |
 8. Уравнение 8. Уравнение |
Уравнение. Правила
| Если в равенство входит буква, то равенство называется уравнением. Уравнение может быть верным при одних значениях этой буквы и неверным при других ее значениях. Например, уравнение x + 6 = 7 верно при x = 1 и неверно при x = 2 . Значение буквы, при котором уравнение — верно, называют корнем уравнения. Например, корнем уравнения x + 2 = 5 является число 3 . Решить уравнение — значит найти все его корни или убедиться, что оно не имеет решения. |
| Пример 1. Решим уравнение x + 28 = 42 . Решение: С помощью вычитания, найдем неизвестное слагаемое. x = 42 – 28, то есть x = 14 . Число 14 является корнем уравнения x + 28 = 42 , потому что 14 + 28 = 42 . Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. |
| Пример 2. Решим уравнение y – 17 = 88 . Решение: y = 17 + 88 , то есть y = 105 . Число 105 является корнем уравнения y – 17 = 88 , так как верно равенство 105 – 17 = 88 . Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность. |
| Пример 3. Решим уравнение 44 – z = 27 . Решение: z = 44 – 27 , то есть z = 17 . Число 17 является корнем уравнения 44 – z = 27 , так как верно равенство 44 – 17 = 27 . Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность. |
| Задача. Два арбуза весят 14 кг, причем масса одного из них равна 8 кг. Какова масса второго арбуза? Решение: Обозначим массу второго арбуза буквой х . Так как масса двух арбузов равна 14 кг, получаем: х + 8 = 14 . Найдем такое значение x , при котором это равенство будет верно. Нам надо найти слагаемое по сумме и второму слагаемому. х = 14 – 8 ; х = 6 . О т в е т: Масса второго арбуза равна 6 кг. |
| Умножение и деление натуральных чисел |
 9. Умножение натуральных чисел и его свойства 9. Умножение натуральных чисел и его свойства |
 10. Деление натуральных чисел и его свойства 10. Деление натуральных чисел и его свойства |
 11. Деление с остатком 11. Деление с остатком |
 12. Порядок выполнения действий 12. Порядок выполнения действий |
 13. Упрощение выражений 13. Упрощение выражений |
 14. Степень числа. Квадрат и куб числа 14. Степень числа. Квадрат и куб числа |
Деление с остатком. Правила
Не всегда одно натуральное число делится нацело на другое натуральное число. Например: У нас есть 85 конфет. Как нам разделить их на семь человек? В данном случае: 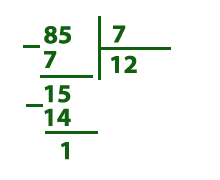 85 — делимое. 7 — делитель. 12 — неполное частное. 1 — остаток. Каждому достанется по двенадцать штук иодна конфета останется. 85 — делимое. 7 — делитель. 12 — неполное частное. 1 — остаток. Каждому достанется по двенадцать штук иодна конфета останется. |
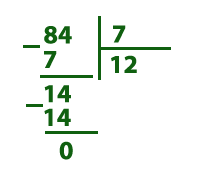 Остаток обязательно должен быть меньше делителя. Если в остатке нуль, то делимое делится на делитель нацело (без остатка). Остаток обязательно должен быть меньше делителя. Если в остатке нуль, то делимое делится на делитель нацело (без остатка). |
| Если нам надо найти делимое, зная делитель, неполное частное и остаток. Надо перемножить делитель и неполное частное и прибавить остаток. Если делитель = 7 , неполное частное = 12 , а остаток = 1 , то делимое = 7 • 12 + 1 = 85 . |
Окружность и круг. Правила
| Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R . Центр окружности обозначают буквой O. Окружность разделяет плоскость на две части, внутреннюю и внешнюю. Внутренняя часть, включающая саму окружность, называется кругом.(Наведите курсор на рисунок.) Точка O — это центр и круга и окружности. |
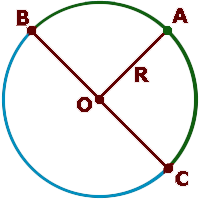 Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет круг на два полукруга, а окружность на две полуокружности. Диаметр равен двум радиусам, это хорошо видно на рисунке. BC = OC + OB , так как BC = D а OC = OB = R , то D = 2R . Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет круг на два полукруга, а окружность на две полуокружности. Диаметр равен двум радиусам, это хорошо видно на рисунке. BC = OC + OB , так как BC = D а OC = OB = R , то D = 2R . |
Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг. Дуга окружности — это часть окружности ограниченная двумя точками. На рисунке точки B и C разделили окружность на две дуги, голубую изеленую. Записать их названия мы можем так:  BC (дуга BC) — в данном случае речь может идти как о голубой так и о зеленой; BC (дуга BC) — в данном случае речь может идти как о голубой так и о зеленой;  BAC (дуга BAC) — в данном случае речь идет именно о зеленой дуге. BAC (дуга BAC) — в данном случае речь идет именно о зеленой дуге. |
Единичного отрезка ОЕ .
Совпадает с единицей.
Сравнение дробей. Правила
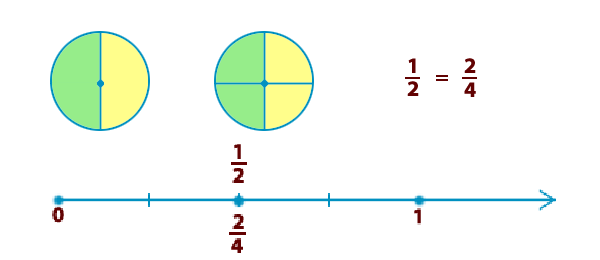 На рисунке вы видите круг, разделенный на четыре части. Две части вместе, например желтые, составляют половину круга. Делаем вывод, что На рисунке вы видите круг, разделенный на четыре части. Две части вместе, например желтые, составляют половину круга. Делаем вывод, что = . | ||||
При сравнении дробей надо руководствоваться следующими правилами. 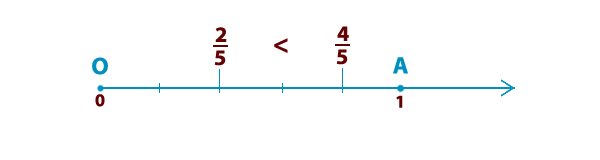 Если у дробей одинаковые знаменатели, большей дробью будет та, у которой числитель больше. Если у дробей одинаковые знаменатели, большей дробью будет та, у которой числитель больше. | ||||
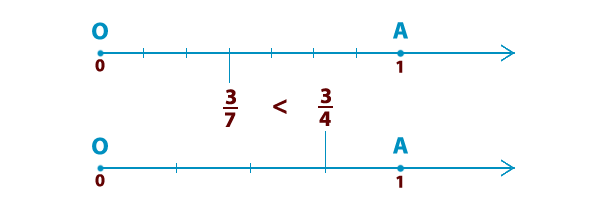 Если у дробей одинаковые числители, то большей дробью будет та, у которой знаменатель меньше. На координатном луче меньшая дробь находится левее, а большая правее. Если у дробей одинаковые числители, то большей дробью будет та, у которой знаменатель меньше. На координатном луче меньшая дробь находится левее, а большая правее. |
Круга.
+
=
;
+
=
.
В буквенном виде выражение сложения дробей выглядит так:
| a |
| c |
+
| b |
| c |
=
| a+b |
| c |
.
–
=
;
–
=
.
В буквенном виде вычитание дробей записывают так:
| a |
| c |
–
| b |
| c |
=
| a−b |
| c |
.
Деление и дроби. Правила
Математическую операцию деление вы уже знаете хорошо. До сих пор мы делили большее число на меньшее, а можно ли меньшее число разделить на большее. Рассмотрим пример из жизни. 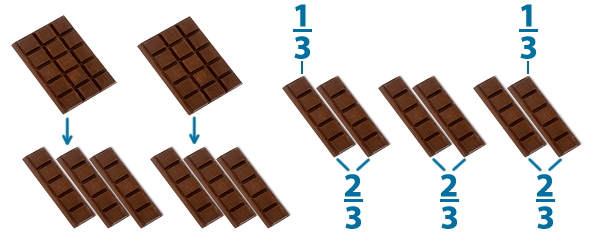 У нас есть две плитки шоколада, а желающих ими полакомиться трое. Разломим каждую плитку на три части и получим 6 частей. Каждая часть — это У нас есть две плитки шоколада, а желающих ими полакомиться трое. Разломим каждую плитку на три части и получим 6 частей. Каждая часть — это |
Смешанные числа. Правила
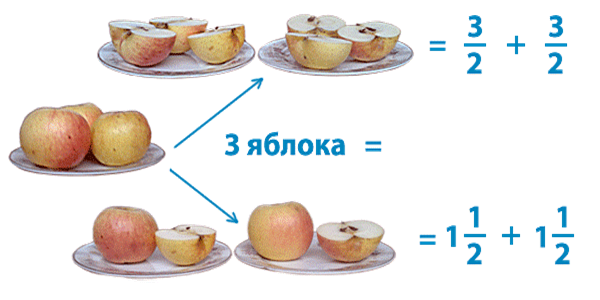
| Предположим, нам надо разделить три яблока поровну между двумя детьми. Мы можем сделать это двумя способами. Во-первых, можно разрезать каждое яблоко пополам и разделить полученные 6 половинок на 2 (половина —– это яблока), + + = . = 1 . является смешанным числом и равняется сумме ) . = 2 + . | ||||||||||||||||||||||||||||
| Научимся переводить неправильную дробь в смешанное число. Например, возьмем дробь . Разделим 7 на 3 . В целую часть, . = 2 ; = 1 ; = 4 . | ||||||||||||||||||||||||||||
| Чтобы выделить целую часть в смешанном числе, поступают следующим образом: 6 = 6 + 1 = 7 . | ||||||||||||||||||||||||||||
| При сложении смешанных чисел целые части складывают отдельно, а дробные отдельно. Не забудьте выделить целую часть, если дробь при сложении получилась неправильная. 2 + 3 = 2 + 3 + + = 5 + = 5 + 1 = 6 . – 1 = 2 – 1 = (2 – 1) + ( – ) = 1 . |
| Десятичные дроби. Сложение и вычитание десятичных дробей |
 25. Десятичная запись дробных чисел 25. Десятичная запись дробных чисел |
 26. Сравнение десятичных дробей 26. Сравнение десятичных дробей |
 27. Сложение и вычитание десятичных дробей 27. Сложение и вычитание десятичных дробей |
 28. Приближенные значения чисел. Округление чисел 28. Приближенные значения чисел. Округление чисел |
Проценты. Правила
| Одна сотая часть любой величины или числа называется процентом. 1% (один процент) = = 0,01 ; = 0,05 ; = = 0,2 ; = 0,33 . | ||||||||||
| Найдем 20% от 300 : 1-ый способ: 20% от 300 = 300 : 100 • 20 = 60 ; 2-ой способ: 20% от 300 = 0,20 • 300 = 60 . | ||||||||||
| Задача №1: В классе 25 учеников, 40% (сорок процентов) из них девочки. Сколько девочек в классе? Решение: 25 : 100 • 40 = 10 девочек ; или 25 • 0,40 = 10 девочек ; О т в е т : в классе 10 девочек. | ||||||||||
| Задача №2: В саду растет 5 кустов желтых роз. Это составляет 25% от всех роз в саду. Сколько кустов роз в саду? Решение: 5 : 25 • 100 = 20 кустов роз; или 5 : 0,25 = 20 кустов роз; О т в е т : в саду растет 20 кустов роз. | ||||||||||
| Задача №3: На стоянке стоит 40 машин, 8 из них фирмы Рено. Какой процент машин фирмы Рено от всех стоящих на стоянке? Решение: 8 : 40 • 100 = 20 % . О т в е т : на стоянке 20% машин фирмы Рено. |
Натуральные числа. Правила
| Для счёта предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: О, 1, 2, 3, 4, 5, 6, 7, 8, 9. Например: триста двадцать восемь - 328 пятьдесят тысяч четыреста двадцать один - 50421 Такую запись чисел называют десятичной. |
| Последовательность всех натуральных чисел называют натуральным рядом: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ... |
| Самое маленькое натуральное число — единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нем нет. |
| Значение цифры зависит от ее места в записи числа. Например 375: цифра 5 означает: 5 единиц, она на последнем месте в записи числа (в разряде единиц), цифра 7 - десятки, она находится на предпоследнем месте (в разряде десятков), цифра 3 - сотни, она стоит на третьем месте от конца (в разряде сотен) и т. д. |
| Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа "нуль". Это число означает "ни одного". Помните! Нуль не относят к натуральным числам. |
| Если запись натурального числа состоит из одного знака — одной цифры, то его называют однозначным. Например, числа 1, 5, 8 — однозначные. Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным. числа 14, 33, 28, 95 — двузначные, числа 386, 555, 951 — трехзначные, числа 1346, 5787, 9999 — четырехзначные и т. д. |
Отрезок. Длина отрезка. Треугольник. Правила
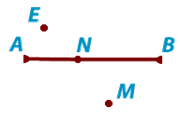 Две точки A и B соединенные прямой линией называются отрезком АВ. Тот же отрезок можно обозначить ВА. Точки А и В называют концами отрезка AB. Любые две точки можно соединить только одним отрезком. На рисунке изображен отрезок АВ. Точка N лежит на этом отрезке между точками A и B, а точки E и M на нем не лежат. Точка N разделяет отрезок AB на два отрезка AN и NB. Их также можно назвать NA и BN. Две точки A и B соединенные прямой линией называются отрезком АВ. Тот же отрезок можно обозначить ВА. Точки А и В называют концами отрезка AB. Любые две точки можно соединить только одним отрезком. На рисунке изображен отрезок АВ. Точка N лежит на этом отрезке между точками A и B, а точки E и M на нем не лежат. Точка N разделяет отрезок AB на два отрезка AN и NB. Их также можно назвать NA и BN. |
| Математическая запись принадлежности точек выглядит так: N ∈ AB — N принадлежит отрезку AB ; A ∈ AB — A принадлежит отрезку AB ; E ∉ AB — E не принадлежит отрезку AB . |
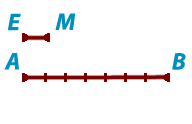 На рисунке изображен отрезок ЕM длиной 1 см. Если отрезок AВ на том же рисунке состоит из семи частей, равных отрезку EM, то длина отрезка АВ равна 7 см. Пишут: АВ = 7 см Длину отрезка AB называют также расстоянием между точками А и В. На рисунке изображен отрезок ЕM длиной 1 см. Если отрезок AВ на том же рисунке состоит из семи частей, равных отрезку EM, то длина отрезка АВ равна 7 см. Пишут: АВ = 7 см Длину отрезка AB называют также расстоянием между точками А и В. |
| Для измерения длин кроме сантиметра применяют и другие единицы длины. Десять сантиметров называют дециметром: 10 см = 1 дм Сто сантиметров называют метром: 100 см = 1 м Один сантиметр равен десяти миллиметрам: 1 см = 10 мм Большие расстояния измеряют в километрах. Один километр равен одной тысяче метров: 1 км = 1000 м |
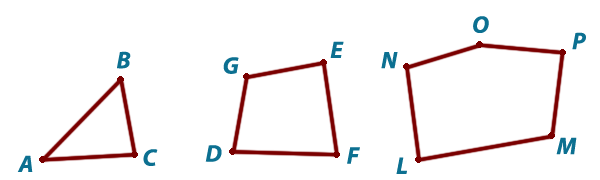 Отрезки АВ, ВС и АС на рисунке вместе составляют треугольник ABC и называются его сторонами, а точки А, В и С — вершинами треугольника ABC. На этом же рисунке изображены четырехугольник DGEF и пятиугольник LNOPM. Вершинами четырехугольника являются точки D, G, E и F, а его сторонами — отрезки DG, GЕ, EF и FD. Такие фигуры, как треугольник, четырехугольник и т. д., называют многоугольниками. Отрезки АВ, ВС и АС на рисунке вместе составляют треугольник ABC и называются его сторонами, а точки А, В и С — вершинами треугольника ABC. На этом же рисунке изображены четырехугольник DGEF и пятиугольник LNOPM. Вершинами четырехугольника являются точки D, G, E и F, а его сторонами — отрезки DG, GЕ, EF и FD. Такие фигуры, как треугольник, четырехугольник и т. д., называют многоугольниками. |