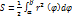Алгоритм нахождения наиб и наим значения функции на отрезке.
1. Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a; b].
2. Определяем все стационарные точки, попадающие в отрезок [a; b]. Для этого, находим производную функции, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни.
3. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
4. Вычисляем значения функции в отобранных стационарных точках (если таковые имеются), а также при x = a и x = b.
5. Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми.
10) Достаточное условие выпуклости (вогнутости). Если вторая производная дважды дифференцируемой функции положительна (отрицательна) на множестве X, то функция выпукла вниз (вверх) на этом множестве.
11) Необходимое условие точек перегиба. Вторая производная f''(x) дважды непрерывно дифференцируемой функции в точке перегиба x0 равна нулю, т.е. f''(x0) = 0.
12) Достаточное условие точек перегиба.Если вторая производная дважды дифференцируемой функции при переходе через точку x0, в которой f''(x0) = 0 меняет свой знак, то x0 есть точка перегиба ее графика.
6.Дифференциальное исчисление функций нескольких переменных.
Частными производными функцииz = f(x,у) называются пределы отношения приращений функции z = z(х,у) к приращению соответствующего аргумента по направлениям ох или оу при Δх → 0 и Δу → 0 соответственно:
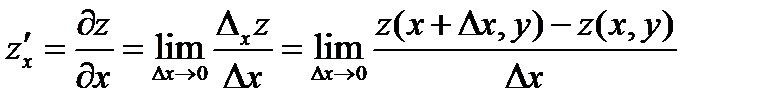 Частная производная по х:
Частная производная по х:
при вычислении считают у = const.
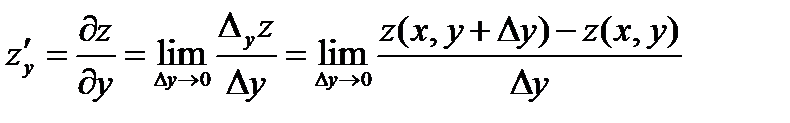 Частная производная по у:
Частная производная по у:
при вычислении считают x = const.
Множество G всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.
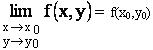 Функция z = f(x,y) называется непрерывной в точке M0(x0,y0), если она определена в этой точке и ее окрестности и выполняется
Функция z = f(x,y) называется непрерывной в точке M0(x0,y0), если она определена в этой точке и ее окрестности и выполняется
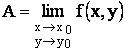
Число A называется пределом функции z = f(x,y) в точке M0(x0,y0):

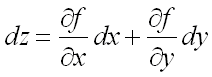 Линейная (относительно дельта икс и дельта игрик) часть полного приращения функции называется полным дифференциаломи обозначается dz:
Линейная (относительно дельта икс и дельта игрик) часть полного приращения функции называется полным дифференциаломи обозначается dz:
где дэикс и дэигрик – дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям
Точка (х0; у0) называется точкой максимума функции z=f(x; y), если всюду в окрестности точки (х0; у0) для
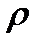 =
= 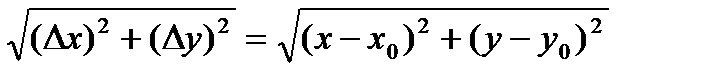 <δ
<δ 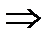 f(x; y)≤ f(х0; у0).
f(x; y)≤ f(х0; у0).
Точка (х0; у0) называется точкой минимума функции z = f(x; y), если всюду в окрестности точки (х0; у0) для
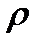 =
= 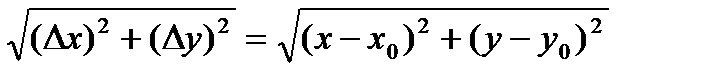 <δ
<δ 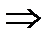 f(x; y) ≥ f(х0; у0).
f(x; y) ≥ f(х0; у0).
Пусть имеется поверхность, заданная уравнением 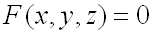 . Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку
. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку 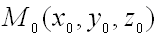 , называется касательной плоскостью к поверхности в точке М0.
, называется касательной плоскостью к поверхности в точке М0.
Прямая, проведенная через точку 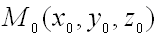 поверхности
поверхности 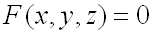 , перпендикулярно к касательной плоскости называется нормалью к поверхности.
, перпендикулярно к касательной плоскости называется нормалью к поверхности.
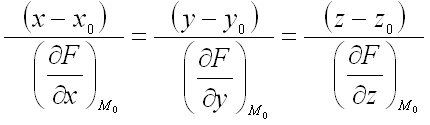 Если поверхность задана уравнением
Если поверхность задана уравнением 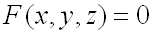 , то уравнение касательной плоскости к этой поверхности в точке
, то уравнение касательной плоскости к этой поверхности в точке 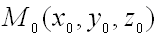 записывается в виде:
записывается в виде: 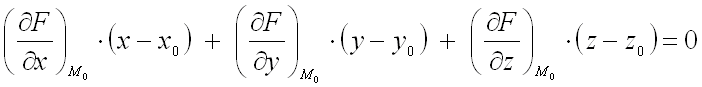 , а уравнение нормали к поверхности в этой же точке – в виде:
, а уравнение нормали к поверхности в этой же точке – в виде:
Необходимые условия дифференцируемости:если функция f дифференцируема в точке х0,то у неё в этой точке существуют частные производные по всем переменным.если функция f дифференцируема в точке х0 ,то она непрерывна в этой точке.
Достаточное условия дифференцируемости: Пусть функция f() определена в некоторой окрестности точки х0. Пусть у функции в этой окрестности существуют непрерывные частыне производные по всем переменным, тогда функция f дифференцируема в этой точке.
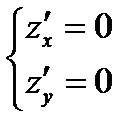 Необходимые условия существования экстремума: или хотя бы одна частная производная не существует.
Необходимые условия существования экстремума: или хотя бы одна частная производная не существует.
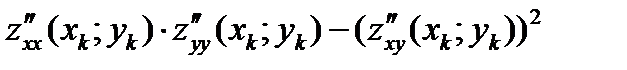
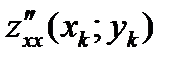 Достаточные условия существования экстремума функции двух переменных: Если> 0
Достаточные условия существования экстремума функции двух переменных: Если> 0
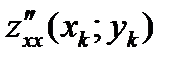 то при а) > 0 функция имеет минимум (min)
то при а) > 0 функция имеет минимум (min)
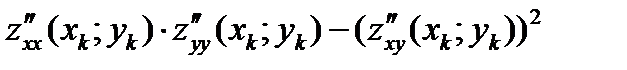 в) < 0 функция имеет максимум (max)
в) < 0 функция имеет максимум (max)
Если<0то экстремума нет.
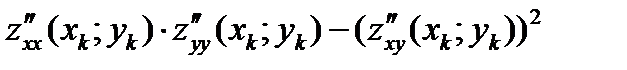
Если= 0, то необходимо дополнительное исследование с помощью производных более высоких порядков.
Комплексныечисла
Определения:
1) Комплексное число - расширение множества вещественных чисел, обычно обозначается 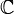 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма 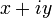 , где
, где 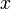 и
и 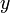 — вещественные числа,
— вещественные числа, 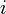 — мнимая единица.
— мнимая единица.
2) Запись комплексного числа 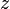 в виде
в виде 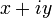 ,
, 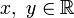 , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.
3) Угол 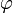 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу 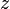 , называется аргументом числа
, называется аргументом числа 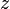 и обозначается
и обозначается 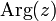 .
.
4) Модулем комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа 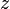 обозначается
обозначается 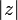 и определяется выражением
и определяется выражением 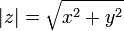 . Часто обозначается буквами
. Часто обозначается буквами  или
или 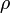 . Если
. Если 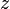 является вещественным числом, то
является вещественным числом, то 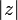 совпадает с абсолютной величиной этого вещественного числа.
совпадает с абсолютной величиной этого вещественного числа.
5) Если комплексное число 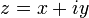 , то число
, то число 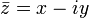 называется сопряжённым (или комплексно сопряжённым) к
называется сопряжённым (или комплексно сопряжённым) к 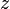 (обозначается также
(обозначается также 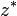 ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
6) Если вещественную 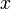 и мнимую
и мнимую 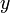 части комплексного числа выразить через модуль
части комплексного числа выразить через модуль 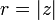 и аргумент
и аргумент 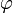 (
( 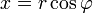 ,
, 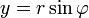 ), то всякое комплексное число
), то всякое комплексное число 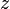 , кроме нуля, можно записать в тригонометрической форме
, кроме нуля, можно записать в тригонометрической форме
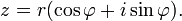
7) Опреденеиепроизведения комплексных чисел устанавливается с таким расчетом, чтобы числа a + b·i и a′ + b′·i можно было перемножать как алгебраические двухчлены, и чтобы число i обладало свойством i2=−1.
8) Пусть 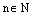 – произвольное натуральное число. Корнем n-ой степени из комплексного числа z называется комплексное число
– произвольное натуральное число. Корнем n-ой степени из комплексного числа z называется комплексное число 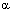 , такое, что
, такое, что 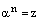 .
.
9) Показательнаяформа записи комплексных чисел
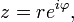 где
где 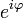 — расширение экспоненты для случая комплексного показателя степени.
— расширение экспоненты для случая комплексного показателя степени.
Свойства и теоремы:
1) Произведением двух комплексных чисел в алгебраической форме называется такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент – сумме аргументов сомножителей.
2) Для того, чтобы перемножить два комплексных числа в тригонометрической формезаписи нужно перемножить их модули, а аргументы сложить. Пусть 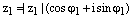 , где
, где 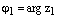 и
и 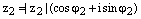 , где
, где 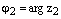 – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда 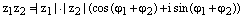 .
.
3) Формула Муавра для комплексных чисел 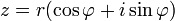 утверждает, что
утверждает, что 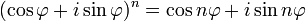 для любого
для любого 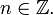
4) Для того, чтобы разделить комплексное число (a1 + b1i ) на другое комплексное число (a2 + b2i ), то есть найти 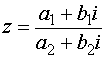 , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
, нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
5) 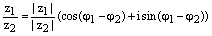
6) 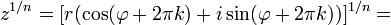
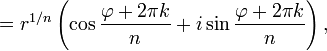
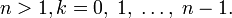
8.Интегральное исчисление функций одной переменной.
1) Первообразная
Функция F(x), дифференцируема на некотором интервале (а,b) называется первообразной для функции f(x) на этом интервале, если для каждого x 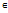 (a,b) справедливо равенство
(a,b) справедливо равенство
F´(x)=f(x)
2) Неопределенный интеграл
Если F(x) является первообразной для функции f(x) на некотором интервале, то выражение F(x)+C называется неопределенным интегралом от функции f(x) и обозначается 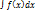
3) Определенный интеграл
Под определенным интегралом 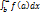 от данной функции f(x) на данном отрезке [a,b] понимается соответствующее приращение ее первообразной, т.е
от данной функции f(x) на данном отрезке [a,b] понимается соответствующее приращение ее первообразной, т.е
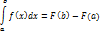
4) Несобственный интеграл от разрывной функции
Пусть функция f(x) непрерывна a ≤x≤b и имеет точку разрыва при x=b. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой
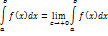
и называется сходящимся или расходящимся в зависимости от того, существует или не существует предел правой части равенства
5) Несобственный интеграл с бесконечным промежутком интегрирования
Пусть функция f(x) непрерывна при a≤x≤b+∞. Тогда по определению
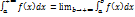 Если предел существует, то интеграл стоящий в левой части равенства, называется сходящимся и его значение определяется формулой; в противном случае равенство теряет смысл, интеграл стоящий слева, называется расходящимся и ему не приписывается никакого числового значения
Если предел существует, то интеграл стоящий в левой части равенства, называется сходящимся и его значение определяется формулой; в противном случае равенство теряет смысл, интеграл стоящий слева, называется расходящимся и ему не приписывается никакого числового значения
Свойства и теоремы
6) Формула интегрирования по частям в неопределенном интеграле
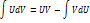
7) Сформулировать правила интегрирования дробно-рациональных функций
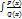 dx
dx
1. Делим числитель на знаменатель
2. Q(x) =(x- 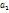 )(x-
)(x- 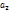 )…
)…
3. Раскладываем дробь на сумму простых дробей 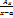 ;
; 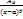 ;
; 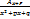 ;
; 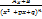 ;
;
1 2 3 4
Интеграл от дробей 1 и 2 типа вычисляется внесением функции под знак дифференциала, 3 и 4 сначала в знаменателе выделяется полный квадрат.
8) Сформулируйте правило интегрирования тригонометрических функций
1. 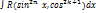
2. t=tg  dx=
dx= 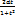
cosx = 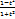 sinx=
sinx= 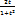
9) С формулировать свойства определенного интеграла
1. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е 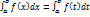
2. Определенный интеграл с одинаковыми пределами равен нулю 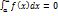
3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный 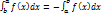
4. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутку [a,b] , равен сумме определенных интегралов, взятых по всем его частичным промежуткам 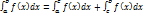
5. Постоянный множитель можно выносить за знак определенного интеграла 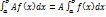
6. Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций 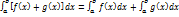
10) Формула Ньютона-Лейбница
Если f непрерывна на отрезке [a,b] и F- ее любая первообразная на этом отрезке, то имеет место равенство 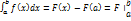
11) Формула интегрирования по частям в определенном интеграле
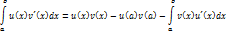
Для краткости употребляется обозначение 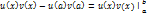
2) Сформулировать свойства неопределенного интеграла
1. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции
2. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого
3. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла
4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от этих функций
5) Замена переменной в неопределенном интеграле
Пусть требуется найти интеграл 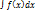 . Введем новую переменную t, положив x=
. Введем новую переменную t, положив x=  (t), где
(t), где  (t)- непрерывная функция с непрерывной производной, имеющая обратную функцию t=Ψ(t). Тогда
(t)- непрерывная функция с непрерывной производной, имеющая обратную функцию t=Ψ(t). Тогда 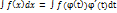 причем в правой части после интегрирования следует сделать подстановку t=Ψ(x)
причем в правой части после интегрирования следует сделать подстановку t=Ψ(x)
3) Таблица интегралов
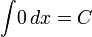
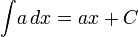
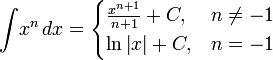
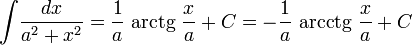
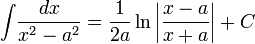
Логарифмы
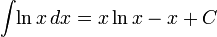
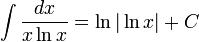
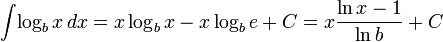
Экспоненциальные функции
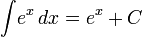
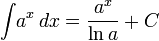
Иррациональные функции
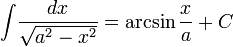
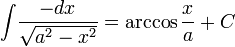
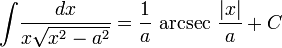
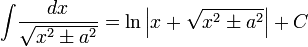
Тригонометрические функции
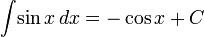
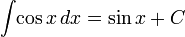
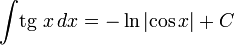
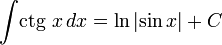
12) Замена переменной в определенном интеграле
Функция f(x) непрерывна на отрезке [a,b], функция x=  (t) имеет на отрезке [
(t) имеет на отрезке [ 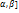 непрерывную производную, при этом a≤
непрерывную производную, при этом a≤ 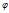 (t)≤b и
(t)≤b и 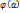 =а,
=а, 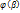 =b
=b
Тогда 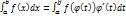
13) Вычисление площади плоской фигуры
Пусть функция f(x) непрерывна на отрезке [a,b]. Если при этом f(x)≥0 на [a,b], то площадь криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:
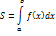
Если же f(x)≤0 на [a,b], то –f(x)≥0 на [a,b]. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле
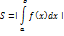
В полярных координатах