Невырожденные системы. Матричный метод решения невырожденных систем. Правило Крамера.

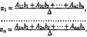
Пустьдана система n линейных уравнений с n неизвестными.

или в матричной форме А*Х=В.Основная матрица А такой системы квадратная. Определитель этой матрицы

называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.

Найдем решение данной системы уравнений в случае D¹0

Умножив обе части уравнения А*Х=В слева на матрицу A^-1, получим

A^-1*A*X=A^-1*BПоскольку. A^-1*A=E и Е*Х=Х , то

X=A^-1*B (4.1)

Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов

Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.

Матричное равенство (4.1) запишем в виде

то есть

Отсюда следует, что

Но 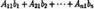есть разложение определителя

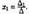по элементам первого столбца. Определитель D получается из определителяD путем замены первого столбца коэффициентов столбцом из свободных членов. Итак, Аналогично: , где D₂ получен из D путем замены второго столбца коэффициентов столбцом из свободных членов: ,...,

Формулы 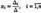называются формулами Крамера.

Итак,невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом, либо по формулам Крамера

Правило Крамера.Если в системе 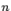линейных уравнений с 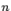неизвестными 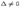, то система имеет решение и притом единственное. Это решение задается формулами

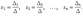
Доказательство. По теореме 14.1 обратная матрица находится по формуле

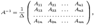
где 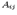-- алгебраические дополнения. Тогда из (15.3) следует, что

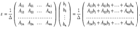Заметим, что по формуле (14.13) разложение определителя по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя 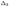по второму столбцу дает второй элемент матрицы-столбца и т.д.

Поэтому

,

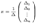откуда и следует утверждение теоремы.

Определение вектора

Вектор АВ^-> – направленный отрезок прямой (АВ) с нач.в т.А и концом в т.В. При умнож.вектора на число «У» получается коллинеарный в-р.

Длина в-ров |АВ|= кв.корень х²+у²

В-ры,лежащие на одной прямой наз-ся коллинеарными. В-ры,лежащие в одной плоскости или ||-ных плоскостях наз-ся компланарными. Если нач.и конец вектора совп.,то в-р наз-ют нулевым. Длина нул.вект.=0.

Вектором,противоп-м в-ру а^->,наз-ся произвед.в-ра а^->на ч-ло (-1),т.е. - а^->=(-1)а^->.

Координатами в-ра а^-> наз-ся корд-ты его конечной точки. На плоскости Oxy два ч-ла - (х;у), в пространстве Oxyz три ч-ла - (х;у;z).

В-р а^-> = (x;y;z) мож.б.записан в виде а^-> = хi^-> +yj^->+zk^->. i^->,j^->,k^-> – единичные в-ры(орты),совпадающие с направл.соотв.осей Ох,Оу,Оz. хi^->,уj^->,zk^-> - компоненты в-ра.

Операции над в-ми:

1) Суммой двух в-ров а^-> и b^-> наз-ся в-р с^->=а^->+ b^->,нач.кот.совп-т с нач.в-ра а^->, а конец – с концом в-ра b^->при усл.,что нач.в-ра b^-> совп.с концом в-ра а^->.

Правило треугольника. Для слож.2-х в-ров а^->и b^-> по правилу треуг-ка оба эти в-ра переносятся ||-но самим себе так,чтобы нач.одного из них совп.с концом другого. Тогда в-р суммы задаётся 3-ей стороной образовавшегося треуг-ка, причём его нач.совп.с нач.первого в-ра.

2)умнож.в-ра на ч-ло:при умнож.в-ра на ч-ло Y пол-ся коллинеарный в-р. (Произвед.в-ра а^-> на ч-ло У наз-ся в-р b^->=Уа^->,имеющий длину |b^->|=|У||а^->|,направление кот.совп.с направл.в-ра а^->, если У<0.) Если b^->= а^->Y,то а^->|| b^->. И наоб.,если а^->|| b^->( а^->не=0),то b^->= а^->Y.

3) Разностью 2-х в-ров а^->и b^-> наз-ся сумма в-ра а^-> и в-ра -b^->,противоположного b^->.

||Скалярным произведением 2-х в-ров наз-ся ч-ло,равное произведению длин этих в-ров на косинус угла между ними: а^-> * b^-> *cosф, где ф-угол между в-рами а^-> и b^->. В-ры явл-ся ||-ми тогда и только тогда, когда их скал.произвед.=0.

||n-мерным в-ром наз-ся упорядоченная совокуп.n действительных чисел,записываемых в виде х=(х₁,х₂,..,х_n),где числа х₁,х₂,х₃,..х_n компоненты в-ра.

Равенство в-ров.Векторы х и y равны тогда и только тогда, когда равны их соотв.компоненты,т.е. х=у,если х_i=у_j, i=1,2,…,n.

Суммой 2-х в-ров одинак.размерности n наз-ся в-р z=x+y,компоненты кот.равны сумме соотв.компонент слагаемых в-ров,т.е.z_i=x_i+y_i,i=1,2,...,n.

Произв-м в-ра на действит.ч-ло Y наз-ся в-р u=Yx,комп-ты кот.равны произв-ю Y на соотв.комп-ты в-ра х,т.е. u_i = Yx_i, i=1,2,...,n.

Линейные оп-ции над люб.в-рами удовлет.след.св-вам: 1)х+у=у+х – коммутативное, 2)(х+у)+z=х+(у+z) – ассоциативное(сочетательное), 3)альфа(бета*х)=(альфа*бета)х, 4)альфа(х+у)=альфа*х+альфа*у, 5)(альфа*бета)х=альфа*х+бета*х, 6)сущ-т нул.в-р 0=(0,0,…,0)такой,что х+0=х для люб.в-ра х., 7)для люб.в-ра сущ-т противоп.в-р (-х) такой,что х+(-х)=0., 8)1*х=х для люб.в-ра х.

Базис

Базис — это линейно независимая совокупность векторов, которая порождает всё пространство. В конечномерном пространстве существует конечный базис, и тогда любой вектор пространства может быть единственным образом представлен в виде разложения вида

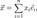где — это базис, а — координаты вектора в заданном базисе.