Решение невырожденных линейных систем. Формулы Крамера
Как известно решение матричного уравнения записывается в виде: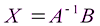 
.
Согласно правилу умножения матриц имеем
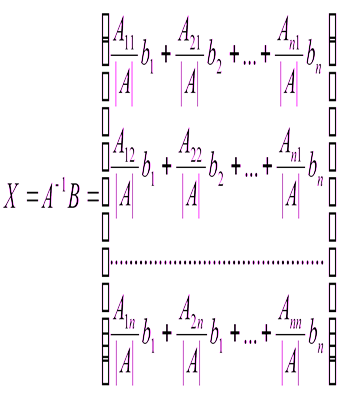
Отсюда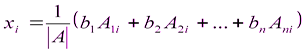 
, i = 1, 2, …, n.
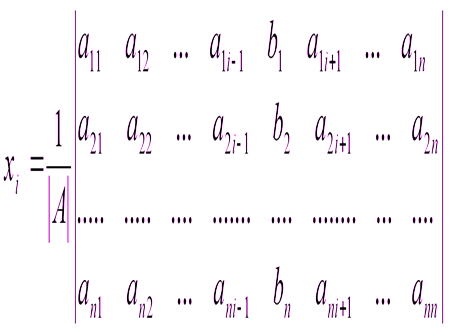
Запишем короче:
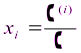, i = 1, 2, …, n,
где 
– определитель системы; 
– определитель 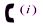матрицы, получаемой из основной матрицы системы заменой её i-го столбца столбцом свободных членов.
Из самого способа решения ясно, что система имеет единственное решение.
Пример.
Система 
имеет определитель 
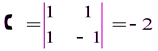отличный от нуля, поэтому имеет единственное решение, которое можно найти по формулам:
, 
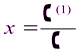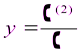, где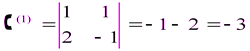 
, 
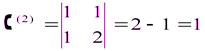, т.е.
, 
.
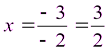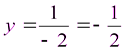10 билет
Если матрица А системы линейных уравнений невырожденная, т.е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A-1B называют матричным способом решения системы, или решением по методу обратной матрицы.
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с 
неизвестными (над произвольным полем):
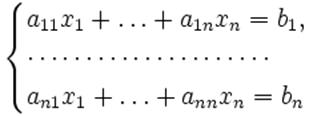
Тогда её можно переписать в матричной форме:
, где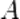 
— основная матрица системы, 
и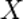 
— столбцы свободных членов и решений системы соответственно:
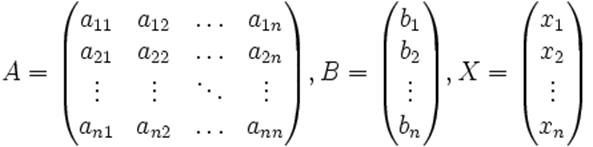
Умножим это матричное уравнение слева на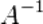 
— матрицу, обратную к матрице : 
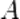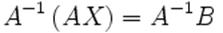
Так как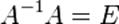 
, получаем 
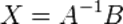. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
.
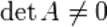Для однородной системы линейных уравнений, то есть когда вектор 
, действительно обратное правило: система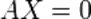 
имеет нетривиальное (то есть ненулевое) решение только если 
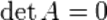. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
11 билет
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].
Описание метода
Пусть исходная система выглядит следующим образом
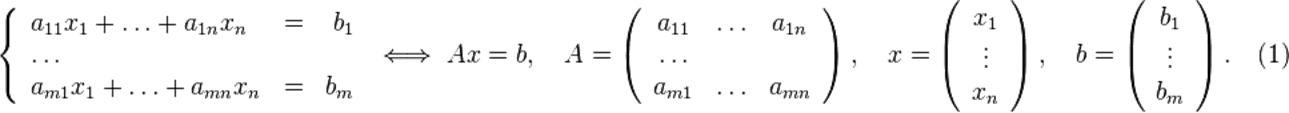
Матрица 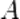называется основной матрицей системы, 
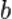— столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):
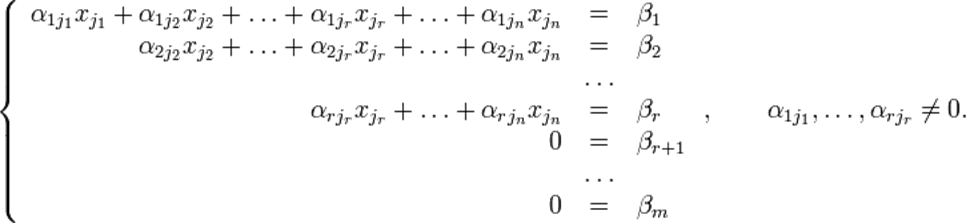
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных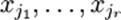 
[3].
Тогда переменные 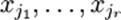называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число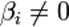 
, где 
, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть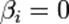 
для любых .
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 
( 
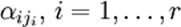, где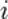 
— номер строки):
,
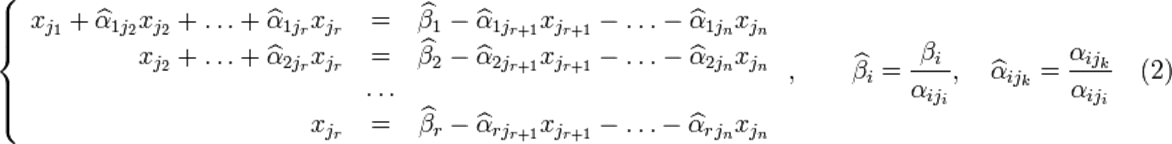где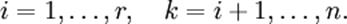 
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
12 билет