Геометрический смысл полного дифференциала.

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х₀, у₀) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х₀, у₀) к точке (х₀+Dх, у₀+Dу).

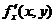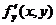Частные производные высших порядков. :Если функция f(x, y) определена в некоторой области D, то ее частные производные и тоже будут определены в той же области или ее части. Будем называть эти производные частными производными первого порядка.

Производные этих функций будут частными производными второго порядка.

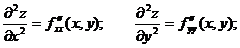Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков. Определение. Частные производные вида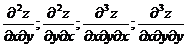 и т.д. называются смешанными производными. Теорема Шварца:

Если частные производные высших порядков ф.м.п. непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования = между собой.

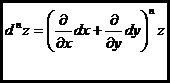Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего с скобках выражения.

14. Уравнение касательной плоскости и нормали к поверхности!

Пусть N и N₀ – точки данной поверхности. Проведем прямую NN₀. Плоскость, которая проходит через точку N₀, называется касательной плоскостью к поверхности, если угол между секущей NN₀ и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN₀.

Определение. Нормальюк поверхности в точке N₀ называется прямая, проходящая через точку N₀ перпендикулярно касательной плоскости к этой поверхности.

В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.

Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М₀(х₀, у₀),касательная плоскость в точке N₀(x₀,y_0,(x₀,y₀)) существует и имеет уравнение:

.

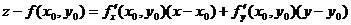Уравнение нормали к поверхности в этой точке:

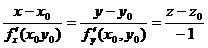
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х₀, у₀) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х₀, у₀) к точке (х₀+Dх, у₀+Dу).

Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.

16. Скалярное поле и его характеристики.Линии ур-ня, производые по направлению,градиент скалярного поля.

Если каждой точке 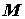пространства ставится в соответствие скалярная величина 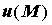, то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также 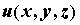или 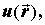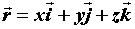Поле может быть плоским, если 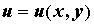центральным 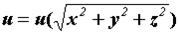(сферическим), если 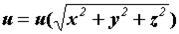цилиндрическим, если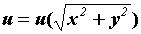

Поверхности и линии уровня: Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых 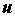принимает постоянное значение. Их уравнение: 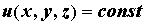. В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение: 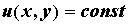В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые.

Производная по направлению и градиент скалярного поля:

Пусть 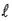единичный вектор с координатами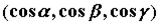 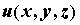- скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле 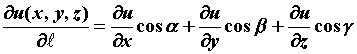Производная по направлению представляет собой скалярное произведение вектора 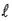и вектора с координатами 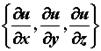, который называется градиентом функции 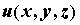и обозначается 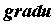.Поскольку 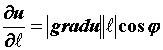, где 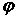угол между 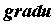и 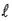, то вектор 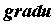указывает направление скорейшего возрастания поля 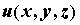а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента:

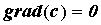
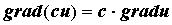
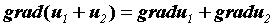
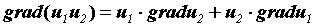
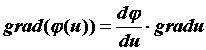
17. Экстремумы ф.м.п.Локальный экстремум ф.м.п., необходимые и достаточные условия его существования . Наибольшее и наименьшее значение ф.м.п. в огран. замкнутой области.

Пусть функция z = ƒ(х;у) определена в некоторой области D, точка N(x0;y0)

Точка (х0;у0) называется точкой максимума функции z=ƒ(х;у), если существует такая d-окрестность точки (х0;у0), что для каждой точки (х;у), отличной от (хо;уо), из этой окрестности выполняется неравенство ƒ(х;у)<ƒ(хо;уо). Аналогично определяется точка минимума функции: для всех точек (х; у), отличных от (х0;у0), из d-окрестности точки (хо;уо) выполняется неравенство: ƒ(х;у)>ƒ(х0;у0). Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами. Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (х0;у0) сравнивается с ее значениями в точках, достаточно близких к (х0; у0). В области D функция может иметь несколько экстремумов или не иметь ни одного.

Необходимые(1) и достаточное(2) условия существования:

(1) Если в точке N(x0;y0) дифференцируемая функция z=ƒ(х;у) имеет экстремум, то ее частные производные в этой точке равны нулю: ƒ'x(х0;у0)=0, ƒ'y(х0;у0)=0. Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Точка, в которой частные производные первого порядка функции z ≈ ƒ(х; у) равны нулю, т. е. f'x=0, f'y=0, называется стационарной точкой функ ции z.

Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками

(2)Пусть в стационарной точке (хо;уо) и некоторой ее окрестности функция ƒ(х;у) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х0;у0) значения A=f''xx(x0;y0), В=ƒ''xy(х0;у0), С=ƒ''уy(х0;у0). Обозначим 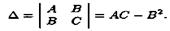Тогда:

1. если Δ > 0, то функция ƒ(х;у) в точке (х0;у0) имеет экстремум: максимум, если А < 0; минимум, если А > 0;

2. если Δ < 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.

3.В случае Δ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования.