Лекция 13. Дифференциальные уравнения первого порядка.

Определение дифференциального уравнения. Основные понятия.

Дифференциальные уравнения первого порядка. Основные понятия. Теорема существования и единственности решения.

Дифференциальные уравнения первого порядка с разделяющимися переменными.

Линейные дифференциальные уравнения первого порядка.

Однородные дифференциальные уравнения первого порядка.

Определение дифференциального уравнения. Основные понятия.

Определение. Уравнение, связывающее независимую переменную x с

неизвестной функцией 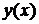и ее производными до некоторого порядка n включительно, называется дифференциальным уравнением 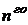порядка.

Общий вид дифференциального уравнения 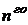порядка: .

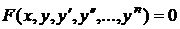Определение. Решением дифференциального уравнения называется функция 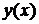, имеющая производные до 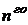порядка включительно и такая, что ее подстановка в уравнение обращает его в тождество.

Определение. Функция, являющаяся решением дифференциального уравнения и зависящая от произвольных постоянных, число которых равно порядку дифференциального уравнения называется общим решением дифференциального уравнения.

Например, для уравнения 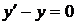функция 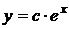является общим решением.

Определение. Решение дифференциального уравнения, полученное из общего, путем придания конкретных значений постоянным, входящим в общее решение, называется частным решением.

Процесс нахождения решения дифференциального уравнения принято называть интегрированием этого уравнения, график решения - интегральной кривой данного уравнения.

Дифференциальные уравнения первого порядка. Основные понятия. Теорема существования и единственности решения.

Определение. Дифференциальным уравнением первого порядка называется уравнение вида 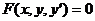(1) или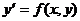

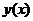Уравнение называется разрешенным относительно производной. Здесь x - независимая переменная, - неизвестная искомая функция, 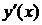- ее производная.

Если при решении дифференциального уравнения получается выражение вида 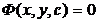, то оно называется общим интегралом уравнения (1) и неявно определяет общее решение дифференциального уравнения (1). Аналогично выражение неявно определяет частное решение уравнения (1).

Начальными условиями для дифференциального уравнения (1) называется пара чисел 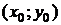, которые записываются так: 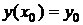. Решить задачу Коши значит найти частные решения дифференциального уравнения, удовлетворяющие заданным начальным условиям.

Теорема Коши.

Если в некоторой окрестности точки 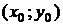функция 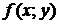определена, непрерывна и имеет непрерывную частную производную , то существует такая окрестность точки 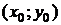, в которой задача Коши имеет решение и притом единственное.

Геометрический смысл решения дифференциального уравнения первого порядка состоит в том, что:

1) общее решение определяет семейство интегральных кривых сплошь заполняющих область существования и единственности решения; 2) частное решение определяет интегральную кривую, выделенную из семейства при конкретном значении 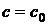; 3) решение задачи Коши с начальными условиями 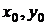- частное решение, проходящее через точку .