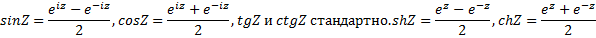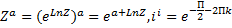Векторные линии векторного поля. Его трубки тока.
Силовая линия – это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой точке. Применяется для визуализации векторного поля, которое сложно изобразить другим способом. Различные виды реальных физических полей имеют свои особенности, которые проявляются в изображении интегральных кривых.
Силовые линии векторного поля, примененные для описания мгновенного поля скоростей жидкости или газа, называют линиями тока. Они изображают картину течения в данный момент времени. Для стационарного течения они совпадают с траекториями частиц. Линии тока, выходящие из замкнутой кривой (не лежащей ни одной своей частью вдоль любой линии тока), образуют трубку тока.
Соленоидальное (трубчатое) поле, векторный потенциал: случай объемно односвязной области.
Пусть Ω – некоторая область пространства 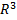 , а=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k – векторное поле, заданное в этой области. Векторное поле а называется соленоидальным (трубчатым), если дивергенция вектора а по области Ω равна нулю: diva=0.
, а=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k – векторное поле, заданное в этой области. Векторное поле а называется соленоидальным (трубчатым), если дивергенция вектора а по области Ω равна нулю: diva=0.
Трехмерная область Ω называется объемно-односвязной, если любая замкнутая кусочно-гладкая самонепересекающаяся ориентированная поверхность S, лежащая в Ω, является границей некоторой области, лежащей в Ω.
Теорема: непрерывно дифференцируемое векторное поле а является соленоидальным в объемно-односвязной области Ω тогда и только тогда, когда потом этого вектора через любую замкнутую кусочно-гладкую самонепересекающуюся ориентированную поверхность S, расположенную в Ω, равен нулю:
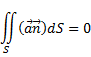
Свойство соленоидального поля: поток соленоидального вектора через поперечные сечения векторной трубки сохраняет постоянную величину. Ее называют интенсивностью векторной трубки.
Дифференциальные операции с оператором «набла».
Вектор с координатами ( 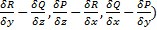 называется ротором или вихрем векторного поля и обозначается символом rota. Введя символический вектор
называется ротором или вихрем векторного поля и обозначается символом rota. Введя символический вектор 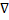 («набла») =
(«набла») = 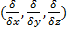 , который называется оператором Гамильтона, ротор векторного поля а можно определить так:
, который называется оператором Гамильтона, ротор векторного поля а можно определить так:
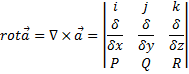
Действия с комплексными числами. Элементарные ФКП.
Комплексные числа – это упорядоченная пара действительных чисел (x,y) – это векторная форма. X=ReZ, y=ImZ
Действия:
1) Сложение: (x1,y1)+(x2,y2)=(x1+x2,y1+y2)
2) Умножение: (x1,y1)*(x2,y2)=(x1x2-y1y2,x1y2+x2y1)
Отождествление: z=(x,0) соотносится с x.
Мнимая единица I; 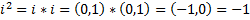
Сложение и умножение комплексных и действительных числе: m+z=(x+m,y), m*z=(mx,my).
Число z представляется в виду x+iy – алгебраическая форма.
Тригонометрическая форма: z=ρ(cosϕ+isinϕ)
Сложение и умножение в алгебраической форме:
Сложение – x1+iy1+x2+iy2=(x1+x2)+i(y1+y2)
Умножение – (x1+iy1)*(x2+iy2)=(x1x2-y1y2)+i(x1y2+x2y1)
ϕ=argZ, ρ=|Z|= 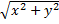 , x=ρcosϕ, y=ρsinϕ
, x=ρcosϕ, y=ρsinϕ
Сопряженная 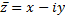 - точка симметричная оси Х.
- точка симметричная оси Х.
Обратное число 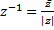
Корень: 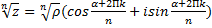
Элементарные функции комплексной переменной:
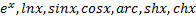
Свойства:
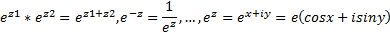
LnZ=ln|Z|+i(argZ+2Пk)