Отклонение относительной частоты от постоянной вероятности

Определение 2. Отношение числа испытаний в которых со­бытие А появилось, к общему числу фактически проведенных испытаний, называют относительной частотой события

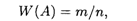
где m — число появлений события A, n — общее число испы­таний.

Разница между вероятностью и относительной частотой состоит в том, что первая вычисляется до опыта, а вторая — после него. Одной из важных характеристик независимых ис­пытаний с постоянной вероятностью появления события А в каждом испытании (0 < р < 1) является отклонение относи тельной частоты от вероятности р. Вероятность того, что это отклонение не превышает по модулю заданного числа ε:

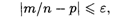
определяется формулой

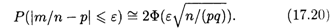
Пример 7. Вероятность получения нестандартной детали р = 0,1. Найти вероятность того, что среди случайно взятых 200 деталей относительная частота появления нестандартной детали отклонится от вероятности р по абсолютной величине не более чем на 0,03.

Решение. В данном случае п = 200, q = 0,9, ε = 0,03. По формуле (17.20) имеем

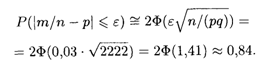
Смысл полученного результата состоит в том, что при доста­точно большом числе проб, каждая из которых содержит 200 случайно выбранных деталей, в 84% случаев отклонение от­носительной частоты от постоянной вероятности р = 0,1 по абсолютной величине не превысит 0,03.

УПРАЖНЕНИЯ

17.1. Найти число способов извлечения из 36 игральных карт двух тузов и двух королей.

17.2. Во взводе служат 32 солдата. Ежедневно для несе­ния караула выделяются по два человека. Можно ли соста­вить расписание караульной службы так, чтобы никакая па­ра военнослужащих этого взвода не несла караульную службу дважды?

17.3. Два букиниста обмениваются друг с другом парами книг. Найти число способов обмена, если первый букинист обмени­вает 6 книг, а второй — 8 книг.

17.4. Абонент забыл две промежуточные цифры номера теле­фона и набрал их наугад. Найти вероятность того, что номер набран правильно в случаях: а) две разные цифры располо­жены в номере рядом; б) обе цифры расположены в разных местах, за исключением первой позиции.

17.5. В урне находится 10 шаров, 7 из которых белые. Найти вероятность того, что из 6 взятых наугад шаров будет 4 белых.

17.6. В ящике имеется 15 деталей, из которых 10 стандартных. Сборщик наугад берет 3 детали. Найти вероятность того, что все взятые детали будут стандартными.

17.7. В урне 40 шаров: 15 белых, 15 красных и 10 синих. Найти вероятность появления цветного шара.

17.8. Абонент забыл первую цифру телефонного номера. Най­ти вероятность того, что при наборе номера наудачу он набе­рет его верно не более чем с трех попыток.

17.9. В лотерее разыгрывается 200 вещевых и 50 денежных вы­игрышей на каждые 10 тыс. билетов. Чему равна вероятность выигрыша вообще?

17.10. В условиях примера 17.7 из урны извлекают один шар, не возвращая его обратно, затем извлекают второй. Найти ве­роятность извлечения из урны во второй раз цветного шара.

17.11. В читальном зале имеется 6 учебников, из которых три нового выпуска. Читатель последовательно, один за другим, взял 2 учебника. Найти вероятность того, что обе взятые книги нового выпуска.

17.12. Три автомашины направлены на перевозку груза. Ве­роятность исправного состояния первой из них составляет 0,7, второй — 0,8 и третьей — 0,5. Найти вероятность того, что все три автомашины находятся в эксплуатации.

17.13. В автохозяйстве имеются две автоцистерны. Вероят­ность технической исправности этих машин составляет соот­ветственно 0,9 и 0,8. Найти вероятность исполнения работы второй автоцистерной заказчику, сделавшему накануне заказ на автоцистерну.

17.14. Инвестор решил вложить поровну средства в три предприятия при условии возврата ему через определенный срок 150% от вложенной суммы каждым предприятием. Вероят­ность банкротства каждого из предприятий 0,2. Найти веро­ятность того, что по истечении срока кредитования инвестор получит обратно по крайней мере вложенную сумму.

Указание. См. формулу (17.11) и пример 1 из п. 17.4.

17.15. При проверке изделия на соответствие стандарту веро­ятность того, что оно пройдет через первого контролера, рав­на 0,55, а через второго — 0,45. Вероятность признания без­дефектного изделия стандартным у первого контролера равна 0,9, а у второго — 0,98. Бездефектное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие прошло через второго контролера.

17.16. В одном из ящиков находится 7 деталей, из которых 3 нестандартные; в другом — 5 деталей, из них 2 нестандарт­ные. Из первого ящика наугад перекладывают деталь во вто­рой ящик, потом из него берут деталь. Найти вероятность то­го, что извлеченная деталь окажется нестандартной.

17.17. Три стрелка выстрелили залпом по цели, и две пули поразили ее. Найти вероятность того, что первый стрелок по­разил цель, если вероятности попадания в цель стрелками со­ответственно равны 0,4, 0,3 и 0,5.

17.18. Определить, что вероятнее для соперников равной силы при игре в шахматы: выиграть одну партию из двух или две партии из четырех.

17.19. Монету бросают пять раз. Найти вероятность выпаде­ния одной из сторон: а) менее двух раз; б) не менее двух раз.

17.20. Вероятность выпуска стандартной детали равна 0,8. Найти вероятность того, что среди 100 деталей будет ровно 75 стандартных.

17.21. Вероятность рождения девочки равна 0,51. Найти ве­роятность того, что среди 100 новорожденных будет ровно 50 девочек.

17.22. Вероятность появления события равна 0,7 в каждом из 2100 независимых испытаний. Найти вероятность появления события: а) не менее 1470 раз; б) не менее 1470 и не более 1500 раз; в) не более 1469 раз.

17.23. Вероятность обращения в поликлинику каждого взрос­лого человека в период эпидемии гриппа равна 0,8. Найти, сре­ди какого числа взрослых человек можно ожидать, что в по­ликлинику будет не менее 75 обращений.

17.24. В банке, осуществляющем кредитование населения, 1000 клиентов. Каждому из клиентов выдается кредит 500 тыс. р. при условии возврата 110% от этой суммы. Ве­роятность невозврата кредита каждым из клиентов в среднем составляет р = 0,01. Какая прибыль гарантирована банку с вероятностью:а) 0,8;б) 0,995?

17.25. Вероятность появления события в каждом из 900 неза­висимых испытаний равна 0,5. Найти вероятность отклонения относительной частоты появления события от его вероятности не более чем на 0,02 по абсолютной величине.