Выпуск оборудования при постоянном темпе роста

Производство оборудования некоторого вида характеризу­ется темпом роста его выпуска

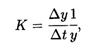
где Δу — прирост выпуска этого оборудования за промежу­ток времени Δt, а у — уровень его производства за единицу времени на момент времени t. Найти общее количество обо­рудования, произведенного к моменту времени t, полагая, что К — известная постоянная величина, единицей времени явля­ется год, а в начальный момент времени t = 0 уровень ежегод­ного производства оборудования составлял у₀.

Решение. Перейдем к пределу при Δt → 0, полагая, что он существует. Будем также полагать, что у является непре­рывной функцией от времени t. Согласно определению произ­водной функции

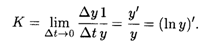
Интегрируя это равенство в пределах от 0 до t, получаем

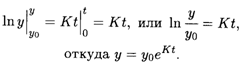
Суммарное количество оборудования, выпущенного за проме­жуток времени t, дается определенным интегралом

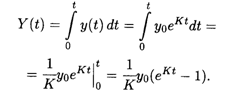
Например, при К = 0,05 (5% ежегодного темпа роста) об­щее количество оборудования, выпущенного за 10 лет, соста­вит

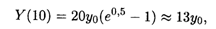
причем уровень производства за указанный период времени увеличится почти на 65%.

Несобственные интегралы

При рассмотрении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция, во-первых, задана на конечном отрезке и, во-вторых, ограничена. Данное выше определение определенного интегра­ла не имеет смысла при невыполнении хотя бы одного из этих условий. Нельзя разбить бесконечный интервал на конечное число отрезков конечной длины; при неограниченной функции интегральная сумма не имеет предела. Тем не менее возможно обобщить понятие определенного интеграла и на эти случаи, с чем и связано понятие несобственного интеграла.

Определение. Пусть функция f(x) определена на промежутке [а, + ) и интегрируема на любом отрезке [a, R], R > 0, так что интеграл

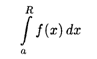
имеет смысл. Предел этого интеграла при R 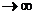называется несобственным интегралом с бесконечным пределом интег­рирования:

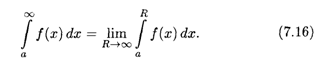
Если этот предел конечен, говорят, что несобственный ин­теграл (7.16) сходится, а функцию f(x) называют интегри­руемой на бесконечном промежутке [а, ); если же предел в (7.16) бесконечен или не существует, то говорят, что несобст­венный интеграл расходится.

Аналогичным образом вводится понятие несобственного интеграла по промежутку (- , b]:

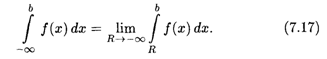
Наконец, несобственный интеграл с двумя бесконечными пре­делами можно определить как сумму несобственных интегра­лов (7.16) и (7.17):

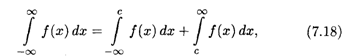
где с — любое число.

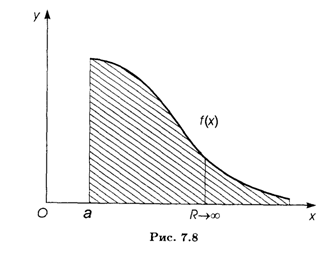
Геометрический смысл несобственного интеграла первого рода заключается в следующем: это площадь бесконечной об­ласти (рис. 7.8), ограниченной сверху неотрицательной функ­цией f(x), снизу — осью Оx, слева — прямой х = а.

Рассмотрим несколько примеров несобственных интегра­лов.

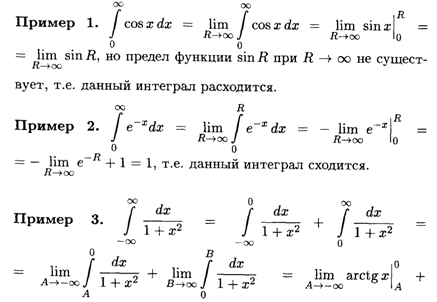
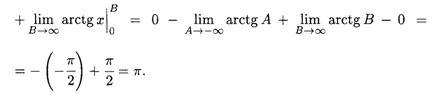
Здесь пришлось разделить исходный интеграл на два и к каж­дому из них применить определение несобственного инте­грала.

Пример 4. 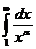, где α — некоторое положительное число.

Решение. Рассмотрим разные случаи для числа α.

1. При α = 1 для любого R > 0 имеем

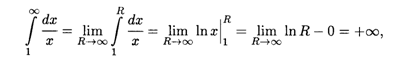
т.е. конечного предела не существует и несобственный интег­рал расходится.

2. При α ≠ 1 для любого R > 0 получаем

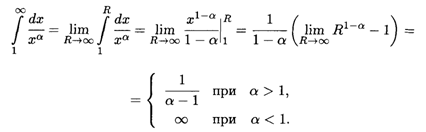
Следовательно, данный интеграл сходится при α > 1 и рас­ходится при α ≤ 1.

В приведенных выше примерах сначала с помощью пер­вообразной вычислялся интеграл по конечному промежутку, а затем осуществлялся переход к пределу. Между тем если для функции f(x) существует первообразная F(x) на всем проме­жутке интегрирования [а, ), то по формуле Ньютона-Лейб­ница

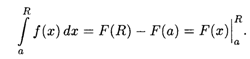
Отсюда следует, что несобственный интеграл существует (схо­дится) в том и только в том случае, когда существует конеч­ный предел

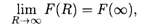
и тогда можно записать:

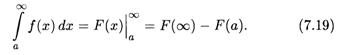
Аналогичный вывод справедлив и для несобственных интегра­лов вида (7.17) и (7.18):

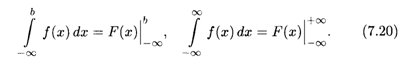
Иными словами, формула Ньютона-Лейбница (основная фор­мула интегрального исчисления) применима и в случае, когда пределы интегрирования бесконечны.

УПРАЖНЕНИЯ

Вычислить определенные интегралы.

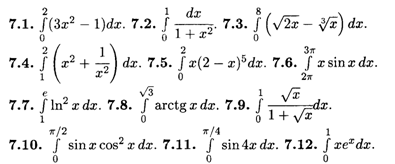
Найти площади фигур, ограниченных следующими линиями.

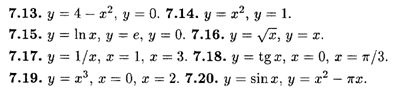
Найти объемы тел, образованных вращением вокруг оси Ох фигуры, ограниченной следующими линиями.

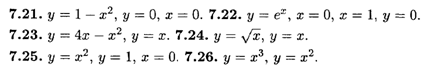
Вычислить несобственные интегралы в случае их сходимости.

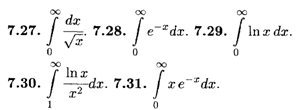
7.32. Найти площадь, заключенную между кривой у = 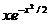и ее асимптотой при х ≥ 0.

7.33. Найти объем тела, образованного вращением вокруг оси Ох дуги кривой у = e^-x от х = 0 до х = + .

Решить задачи с экономическим содержанием.

7.34. Найти стоимость перевозки М т груза по железной доро­ге на расстояние 1 км при условии, что тариф у перевозки одной тонны убывает на а р. на каждом последующем километре.

7.35. Мощность у потребляемой городом электроэнергии вы­ражается формулой

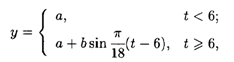
где t — текущее время суток. Найти суточное потребление электроэнергии при а = 15000 кВт, b = 12000 кВт.