Числовые последовательности

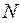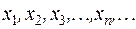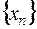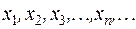Бесконечной числовой последовательностью называется числовая функция натурального аргумента, т.е. функция, определенная на множестве . Она записывается или сокращенно , где – элементы или члены числовой последовательности;

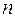– номер члена последовательности;

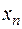– общий или 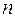-ый член последовательности.

Последовательность считается заданной, если известна формула для .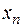

Например,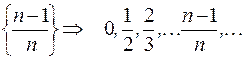

Последовательность 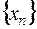называется ограниченной, если существует такое число 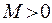, что для любого 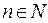выполняется неравенство 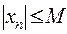, т.е. .

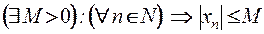Например, 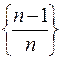– ограничена, так как ;

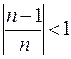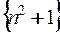– неограничена.

Можно заметить, что члены последовательност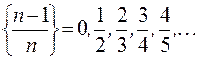и при 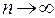, неограниченно приближаются к .

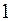В этом случае говорят, что число 1 называется пределом данной последовательности.

Определение. Число 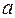называется пределом последовательност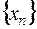и при 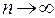, если для любого сколь угодно малого положительного числа 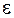найдется такое натуральное число 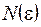(зависящее от 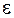), что для всех членов последовательности с номерами 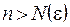выполняется неравенство 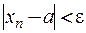. При этом пишут: 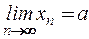и говорят, что последовательность 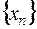сходится к числу .

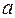Определение можно записать с помощью логических символов:

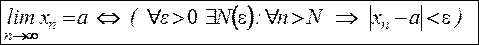
Геометрический смысл предела последовательности.

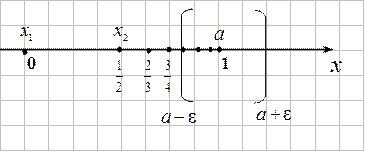Неравенство 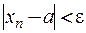равносильно неравенству 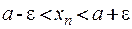, которое показывает, что 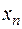принадлежит 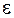– окрестности точки .

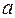Геометрически определение предела последовательности можно сформулировать так:число 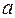называется пределом последовательности 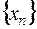, если для любой 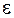– окрестности точки 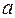найдется такое число 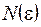, что все значения 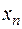, для которых 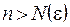, попадут в 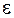– окрестность точки .

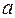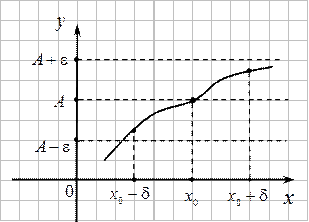
Из рисунка видно, что в 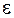– окрестности точки 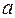находится бесконечное число членов последовательности, а вне ее - конечное число.

Отсюда следует, что сходящаяся последовательность имеет только один предел.

Не всякая последовательность имеет предел. Последовательность, не имеющая предела, называется расходящейся (обозначается ).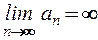

Сформулируем признак существования предела последовательности.

ТеоремаВейерштрасса.Всякая монотонная ограниченная последовательность имеет предел.

Например:

1) Последовательность 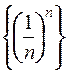– монотонно убывает и ограничена, следовательно, .

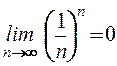2) Последовательность 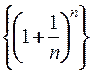– монотонно возрастает и ограничена, следовательно, .

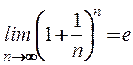Можно показать, что число 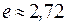, является основанием натурального логарифма .

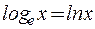Предел функции

Предел функции в точке

Пусть функция 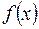определена в некоторой окрестности точки 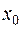, причем в самой точке 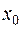функция может быть и не определена.

Определение. Число 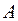называется пределом функции 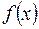в точке 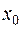( или при 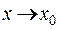), если для любого положительного числа 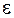найдется такое положительное число 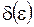, что для всех 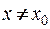, удовлетворяющих неравенству 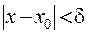, выполняется неравенство 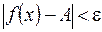. Записывают .

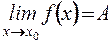Коротко можно записать так:

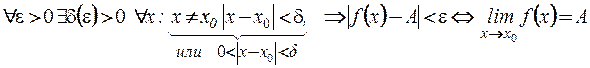
Геометрический смысл:

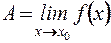, если для любой 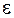– окрестности точки 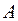найдется такая 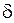– окрестность точки 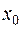, что для всех 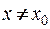из этой 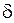–окрестности соответствующие значения функции 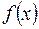лежат в 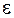– окрестности точки 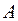. Т.е. точки графика лежат внутри полосы шириной 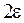, ограниченной линиям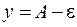и и 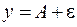. Очевидно, что величина 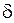зависит от 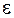. Поэтому пишут .

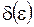Пример 1. Доказать, что .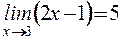

¦ Возьмем произвольное число 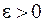. Найдем по этому 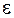такое значение 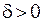, при котором из неравенства 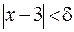следовало бы неравенство 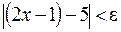. Преобразуя последнее неравенство, получаем 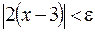или 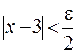. Отсюда видно, что если взять 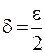, то для всех 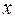, удовлетворяющих 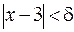, выполняется неравенство 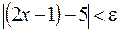. Это и означает, что . ¢

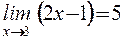Пример 2.Доказать, что .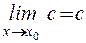

¦ Для любого 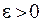можно взять любое 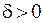. Тогда при 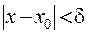, 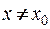имеем . ¢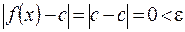

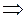
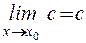6.2. Предел функции при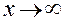

Пусть функция определена на .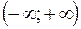

Определение. Число 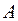называется пределом функци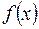и при 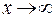, если для любого положительного числа 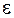существует такое число 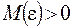, что при всех 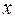, удовлетворяющих неравенству 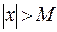, выполняется неравенство 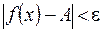. Коротко можно записать так:

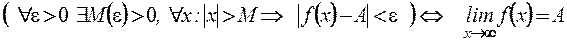
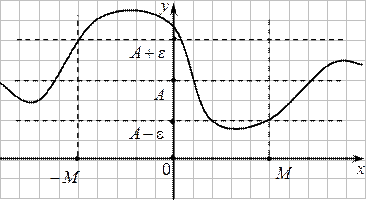Геометрический смыслэтого определения таков: 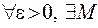, что при 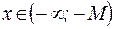или при 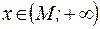соответствующие значения функции 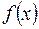попадают в 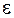– окрестность точки 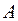, т.е. точки графика лежат в полосе шириной 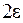, ограниченной прямым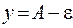и и .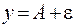

Сформулируем теперь понятие предела функции при .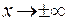

Определение. Число 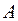называется пределом функции при 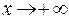(соответственно при 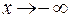), если для любого положительного числа 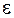существует такое число 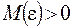, что при всех 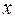, удовлетворяющих неравенству 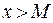(соответственно 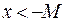), выполняется неравенство .

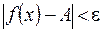Если 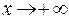, то пишут .

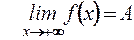Если 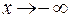, то пишут .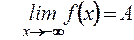