Числовая прямая (числовая ось) и множества на ней

Здесь нам понадобится понятие о соответствии множеств, позже мы еще раз обратимся к нему в разделе о функциональ­ной зависимости. Будем говорить, что между множествами Х и Y установлено соответствие, если по какому-либо закону или правилу каждому элементу х 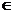Х соответствует элемент у 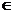Y. Соответствие называется взаимно однозначным, если любому х 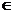Х соответствует только один элемент из Y и, наоборот, любому у 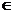Y соответствует только один элемент .

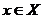Оказывается, что между множеством вещественных чисел и множеством точек на прямой может быть установлено вза­имно однозначное соответствие. Это дает возможность нагляд­но геометрически изобразить вещественные числа на числовой оси. На прямой выберем точку О начала отсчета, укажем на­правление отсчета (обычно слева направо, рис. 1.2) и единицу измерения или масштаб.

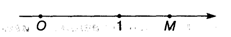
Рис. 1.2

Эти три действия полностью определяют нам числовую (ко­ординатную) ось. На ней вещественные числа изображаются в виде точек. Пусть М — произвольная точка на этой оси. По­ставим ей в соответствие число x, равное по величине длине отрезка ОМ, со знаком +, если точка М находится справа от начала отсчета, или со знаком —, если М расположена слева от точки О. Тогда число х называется координатой точки х. Справедливо и обратное утверждение: каждому вещественно­му числу х соответствует определенная точка на координатной оси, координата которой равна х.

Пусть а и b — два числа, причем а < b. Укажемнекоторыенаиболее употребительные числовые множества:

1) множество всех чисел, удовлетворяющих неравенству а ≤ х ≤ b, называется отрезком (сегментом) и обозначается [а, b];.

2) множество всех чисел, удовлетворяющих строгому неравен­ству а < х < b, называется интервалом и обозначается (а,b);

3) множество всех вещественных (действительных) чисел бу­дем обозначать

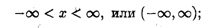
4) аналогично пп. 1-3 можно определить числовые множества типа (a,b], [а, b), (а, + ), (- ,b), [а, + ) и (- , b].

Все эти множества называются промежутками; промежут­ки типа 1 и 2 и первые два из п. 4 называются конечными, а числа а и b — их концами; остальные промежутки называются бесконечными. Промежутки первых двух типов из п. 4 называются полуинтервалами.

Числовым промежуткам соответствуют промежутки на координатной оси. Сегмент [а, b] изображается отрезком М₁М₂, таким, что точка M₁ имеет координату а, точка M₂ — координату b. Вся координатная прямая является изображени­ем множества всех вещественных чисел, и потому множество (- , ) называется числовой прямой (осью), а любое число называется точкой этой прямой.

Грани числовых множеств

Будем говорить, что множество Х ограничено сверху (снизу), если существует число d, такое, что для любого х 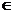Х выполняется неравенство х ≤ d (х ≥ d). Число d тогда называется верхней (нижней) гранью множества X. Множест­ва, ограниченные снизу и сверху, называются ограниченными. Любой конечный промежуток ограничен. Интервалы (а, + ) и (- , b) представляют собой множества, ограниченные соот­ветственно снизу (сверху), но не ограниченные сверху (снизу). Вся числовая прямая не ограничена ни снизу, ни сверху.

Любое ограниченное сверху (снизу) множество имеет бесконечное число верхних (нижних) граней. Действительно, если число d является верхней гранью множества X, то и любое чис­ло d₁ > d, согласно определению верхней грани, также будет верхней гранью этого множества. Наименьшая верхняя грань множества X, ограниченного сверху, называется точной верх­ней гранью этого множества; она обозначается символом supX. Наибольшая нижняя грань ограниченного снизу множества Х называется точной нижней гранью этого множества и обозна­чается символом infX. Эти символы заимствованы из латин­ского языка:supremum — наивысший иinfimum — наиниз­ший.

Приведем некоторые примеры. Пусть Х = (а, b). В таком cлучае числа а и b являются точными нижней и верхней граня­ми множества X, т.е. а = inf X, b = sup X. Пусть X = (- , b). Тогда нижних граней (в том числе и точной нижней грани) множество Х не имеет, а число b является его точной верхней гранью: b = sup X.

Известна следующая теорема о существовании точной верх­ней (нижней) грани числового множества, которую мы приво­дим ниже без доказательства.

ТЕОРЕМА 1. Если непустое числовое множество ограниче­но сверху (снизу), то оно имеет точную верхнюю (нижнюю) грань.

Абсолютная величина числа

Приведем определение абсолютной величины вещественно­го числа х (модуля числа):

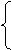х, если х ≥ 0;

|x| =

-х, если х < 0.

Из этого определения следует ряд свойств абсолютной величи­ны, который мы приводим ниже без доказательств.

1. |х| ≥ 0.

2. |х| = | - x|.

3. -|х| ≤ х ≤ |x| .

4. Пусть а — положительное число. Тогда неравенства |х| ≤ а и -а ≤ х ≤ а равносильны.

5. Для любых двух действительных чисел х и у справед­ливо неравенство

|x + y| ≤ |x| + |y|.

В это свойство можно включить также и неравенство

|х – у| ≤ |х| + |у|.

6. Для любых двух действительных чисел х и y справед­ливо неравенство

|х – y| ≥ |х| -|у|.

УПРАЖНЕНИЯ

Определить множества значений x, удовлетворяющих следую­щим условиям.

1.1.|х|<2.1.2. x² ≤ 9.1.3. х² > 25. 1.4. |x – 3| <1.1.5. (x² + l) ≤ 17. 1.6 (x² - 3)≥1.1.7. х - х² > 0.

1.8. x² – 2x + 7 > 0.1.9.x² – 2x + 5 < 0.