Числовая последовательность

Если каждому натуральному n из множества натуральных чисел по некоторому правилу поставить в соответствие действительное число x_n, то множество пронумерованных чисел

x₁, x₂, x₃, …, x_n, … (1)

называется числовой последовательностью.

При этом числа x_i (i = 1, 2, 3, …, n, …) называются членами последовательности, символ x_n — общим членом, а число n является его номером.

Например, общий член x_n задается некоторой формулой x_n = n². Полагая поочередно n = 1, 2, 3, …, получим числовую последовательность 1, 4, 9, … .

Предел и непрерывность функции

Пусть X и Y — некоторые множества, и пусть каждому 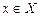поставлен в соответствие по определенному правилу f единственный элемент 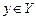. Тогда говорят, что на множестве X задана функция одной переменной со значениями в множестве Y. Обозначение: y = f(x). В этом случае X — область определения функции. Обозначение: D(f).

Всякий интервал, содержащий точку x₀, называется окрестностью точки x₀.

Пусть 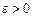. Интервал (x₀ – 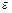; x₀ + 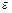) называется 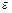-окрестностью точки x₀.

Определение предела функции по Коши. Пусть функция y = f(x) определена в 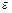-окрестности точки x₀ за исключением, быть может, точки x₀. Тогда, если для любого 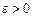, сколь угодно малым бы оно ни было, существует такое 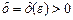, что для всех 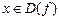, удовлетворяющих неравенству 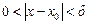, выполняется неравенство 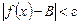, то число B называется пределом функции в точке x₀. Обозначение: .

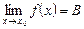Число В называется пределом функции f(x) в бесконечности, если для любого даже сколь угодно малого положительного числа 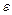найдется такое 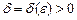, что для всех 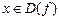, удовлетворяющих неравенству 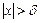, выполняется неравенство 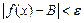. Обозначение: .

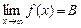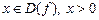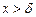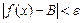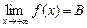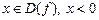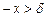Если для всех и выполняется неравенство , то . Если для всех и выполняется неравенств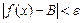о , то .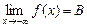

Рассмотрим 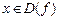, 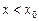( 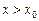). Если существует предел функции при х, стремящемся к х₀, то он называется левым (правым) пределом функции в точке х₀. Обозначение: .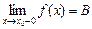

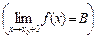Факт существования в точке х₀ предела функции у = f(x) равносилен факту существования в этой точке равных между собой односторонних пределов .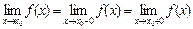

Функция y = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению 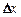аргумента в этой точке соответствует бесконечно малое приращение 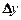функции (рис. 10).

Рис. 10

Функция y = f(x) называется непрерывной в точке х₀, если предел функции в точке х₀ равен значению функции в этой точке, т. е. .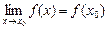

Функция f(x) называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Точки, в которых функция не является непрерывной, называются точками разрыва функции.

Элементарные функции

Основными элементарными функциями называют следующие функции:

1. Постоянную функцию у = с, с — const.

2. Степенную функцию у = х 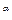, 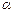— любое действительное число.

3. Показательную функцию у = а^х (0 < a 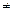1).

4. Логарифмическую функцию .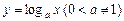

5. Тригонометрические функции y = sin x, y = cos x, y = tg x,
y = ctg x.

6. Обратные тригонометрические функции y = arcsin x, y = arccos x,
y = arctg x, y = arcctg x.

Функцию, аналитическое выражение которой можно получить при помощи конечного числа арифметических операций над основными элементарными функциями, а также при помощи операции взятия функции от функции, назовем элементарной функцией.

Пример.

Функции f(x) = arcsin(log₅(x² + 1)), f(x) = 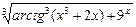, f(x) = 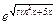являются элементарными.

Областью определения D(y) функции y = f(x) называется множество значений аргумента х, для каждого из которых существует вполне определенное числовое значение функции.

Теорема. Если 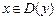элементарной функции y = f(x), то 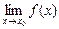= f(x₀).

Например, .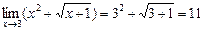

Теоремы о пределах

1. Функция y = f(x) в точке х₀ не может иметь более одного предела.

2. Предел постоянной величины равен самой этой величине, т. е. .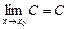

3. Пусть f₁(x) и f₂(x) — функции, для которых существуют пределы при : , .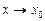

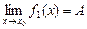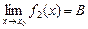Тогда:

3.1. Существует и предел алгебраической суммы этих функций, причем предел этой алгебраической суммы равен алгебраической сумме пределов, т. е.

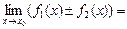
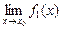
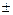
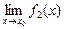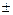= А В.

3.2. Существует и предел произведения этих функций, причем предел этого произведения равен произведению этих пределов:

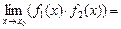
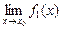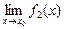· = А·В.

3.3. Если В 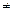0, то существует и предел частного этих функций, причем предел этого частного равен частному пределов, т. е.

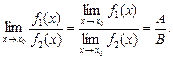
Формулировка для случая, когда 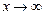, аналогична.

Функция g(x) называется бесконечно малой функцией при 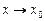( 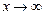), если

.

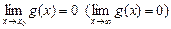Функция f(x) называется бесконечно большой функцией при 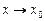( 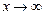), если для любого Р > 0 найдется положительное число 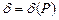, что для всех 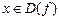, удовлетворяющих условию 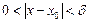( 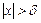), выполняется неравенство 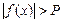. Обозначение: ( ).

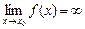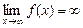Если f(x) 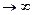при 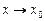и f(x) принимает только положительные (отрицательные) значения, то пишут

.

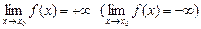Теорема (о связи между бесконечно малыми и бесконечно большими функциями)

Если g(x) — бесконечно малая функция при 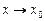( 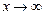), то 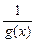— бесконечно большая функция при ( ).

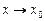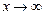Если f(x) — бесконечно большая функция при 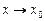( 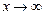), то 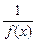— бесконечно малая функция при ( ).

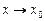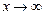Замечательные пределы

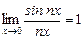— первый замечательный предел.

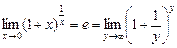— второй замечательный предел ( ).

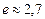Вычисление пределов вида 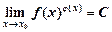(2)

Для вычисления пределов вида (2) вычисляем пределы 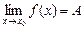, 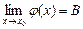. Могут встретиться следующие ситуации:

1. Если А, В — конечные числа, тогда С = А^В.

2. Если А = 1, В = 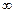, тогда для вычисления предела (2) применяют второй замечательный предел.

Во всех остальных случаях задачу вычисления предела (2) решают непосредственно.