Уравнение Д.Бернулли для элементарной струйки

Реальной жидкости. График уравнения Д.Бернулли

В отличие от идеальной жидкости, в которой работа внешних сил, действующих на жидкость, полностью идет на изменение ее кинетической энергии, благодаря чему происходит преобразование кинетической энергии в потенциальную или наоборот, в реальной жидкости, обладающей вязкостью, часть работы сил, действующих на жидкость, затрачивается на преобразование механической энергии в тепловую.

Если преобразование одной формы механической энергии в другую форму механической энергии является процессом обратимым, то преобразование механической энергии в тепловую, происходящее вследствие сил трения, является процессом необратимым.

Это явление, называемое диссипацией энергии, в гидравлике рассматривается как гидравлическое сопротивление, а величина диссипируемой энергии называется гидравлическими потерями. расчетная форма уравнения баланса энергии имеет вид

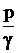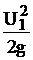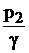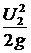z₁+ + = z₁+ + +h_п, (4.6)

где h_п – гидравлические потери.

Уравнение (4.6) представим графически (рис.4.10).

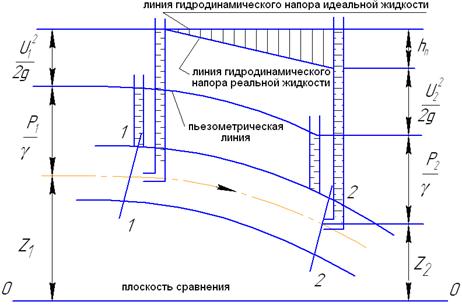
Рис.4.10

Уравнение Д.Бернулли для потока реальной жидкости

Так как поток представлен совокупностью элементарных струек, то его энергия должна быть равна сумме энергий этих струек.

Удельная энергия элементарной струйки

е =z+ 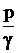+ 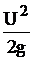, м.

Допустим, что через живое сечение струйки протекает весовой расход 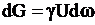Н/с, тогда мощность ее, т.е. энергия в единицу времени будет иметь вид

,

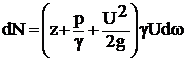Мощность потока

.

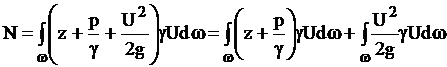Мощность потока от потенциальной энергии можно определить только для плавноизменяющихся потоков, для которых в каждом живом сечении z+ 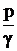= idem, т.е. подчиняется закону гидростатики. В этом случае

.

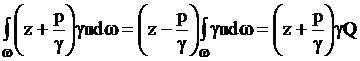Мощность потока от кинетической энергии можно определить, если известен закон распределения скоростей по живому сечению потока, что является сложной задачей, поэтому эту мощность определяют по средней скорости – одинаковой по всему сечению:

.

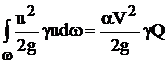Действительная мощность от кинетической энергии несколько больше, чем вычисленная по средней скорости, поэтому для компенсации этого неравенства введен коэффициент Кориолиса α. Численное значение этого коэффициента зависит от режима движения жидкости. Для ламинарного режима α = 2, для турбулентного α=1,05…1,1~1,0.

Тогда расчетная форма уравнения Д.Бернулли для потока реальной жидкости, написанная для единицы веса жидкости, будет иметь вид

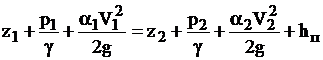. (4.7)

Определение гидравлических потерь

Классификация потерь напора

При движении реальной жидкости неизбежно происходят потери ее энергии, именуемые гидравлическими потерями.

Они вызываются сопротивлениями двух видов:

- сопротивлениями по длине, обусловленными силами трения;

- местными сопротивлениями, обусловленными изменениями скорости потока по величине и направлению (повороты, регулирующая арматура, фильтры и т.п.)

Таким образом, гидравлические потери бывают двух видов: линейные и местные. Формулы для их определения носят эмпирический характер.

Определение гидравлических потерь является одним из важнейших вопросов почти любого гидравлического расчета. Без знания величины гидравлических потерь нельзя определить один из важнейший параметров насоса – напор (давление), следовательно, и мощность энергетического оборудования.