Занятие 5. Системы случайных величин

Законом распределения дискретной двумерной случайной величины (Х,Y) называют перечень возможных значений этой величины, т. е. пар чисел (x_i,y_i) и их вероятностей P_ij. Закон распределения обычно задают в виде таблицы с двойным входом:

X	x1	x2	x3	…	xn
Y
y1	p11	p12	p13	…	p1n
Y2	p21	p22	p23	…	p2n
…	…	…	…	…	…
ym	pm1	pm2	pm3	…	pmn

События ( 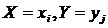) при ( 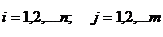) образуют полную группу, поэтому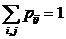

По заданному закону распределения двумерной дискретной величины можно найти законы распределения составляющих. Для того, чтобы найти вероятность события 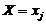или Y=y_i, надо использовать теорему сложения и суммировать вероятности i-го столбца или j-ой строки соответственно

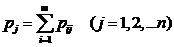и .

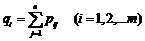X	x1	x2	…	xn
p	p1	p2	…	pn

Y	y1	y2	…	ym
q	q1	q2	…	qm

Функция распределения является универсальным способом задания двумерной случайной величины, пригодным как для дискретных систем, так и для непрерывных.

Функцией распределения системы двух случайных величин (X,Y) называется вероятность совместного выполнения неравенств: X<x и Y<y, т.е.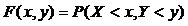

Двумерная случайная величина называется непрерывной, если F(x,y) непрерывна на всей плоскости и существуют частные производные

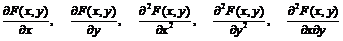непрерывные на всей плоскости, за исключением отдельных точек и линий.

Плотностью совместного распределения вероятностей f(x,y) двумерной непрерывной случайной величины (X,Y) называется вторая смешанная частная производная от функции распределения:

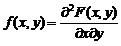
Пример 5.1. Двумерная непрерывная случайная величина (X,Y) задана функцией распределения

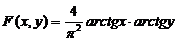
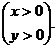Найти плотность совместного распределения .

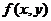Решение. Найдем производные

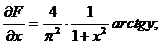
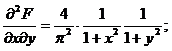
следовательно,

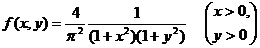
Функция распределения F(x,y) выражается через плотность распределения f(x,y) следующим образом:

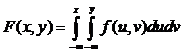
Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:

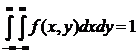
Вероятность попадания случайной точки (X,Y) в область D определяется равенством

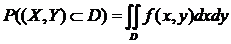
Пример 5.2. Двумерная непрерывная случайная величина (X,Y) задана плотностью распределения вероятнотей

.

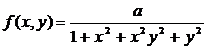Найти: a, 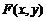и вероятность попадания случайной точки в прямоугольник с вершинами .

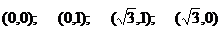Решение.

1. Из условия 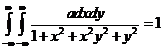найдем параметр a

=

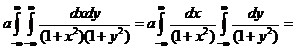
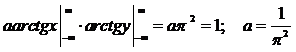
2.

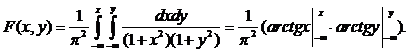
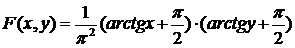
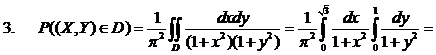
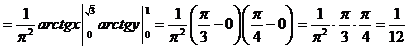
Чтобы найти плотность распределения случайной величины Х, входящей в систему (Х,Y), надо проинтегрировать двумерную плотность f(x,y) по всем возможным значениям случайной величины Y .

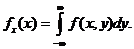Аналогично получается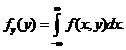

Обратно: по известным плотностям f_х (x) и f_у(y) найти плотность распределения f(x,y) системы в общем случае нельзя. Для решения этой задачи надо еще знать зависимость между этими величинами.

Случайные величины X и Y называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина, т.е. плотность распределения f(x,y) распадается на два множителя, один из которых зависит только от х, а другой только от у. В противном случае величины называются зависимыми.

Пример 5.3. Двумерная случайная величина (X,Y) задана плотностью распределения вероятностей

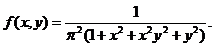. Являются ли случайные величины Х и Y зависимыми?

Решение.Преобразуемf(x,y) , разложив знаменатель на множител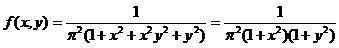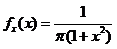и

;

и 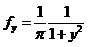, т.е. случайные величины X и Y независимы.

Пример 5.4. Двумерная случайная величина (X,Y) равномерно распределена внутри круга радиуса R с центром в начале координат, т.е. в области D: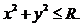

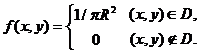
Проверить, будут ли величины X и Y независимы?

Решение.Найдем плотности распределения f_х(x) и f_у(y):

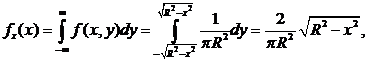
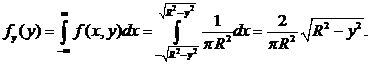
Теперь очевидно, что 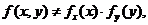т.е величины X и Y зависимы.

Задачи для самостоятельного решения

1. Двумерная случайная величина задана таблицей

Y	Х
0,5	0,1	0,3	0,25
1,5	0,15	0,15	0,05

Найти законы распределения составляющих.

2. Задана функция распределения двумерной случайной величины

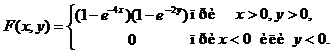
Найти двумерную плотность вероятностей системы.