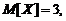Занятие 4. Числовые характеристики непрерывных случайных величин. Равномерное и нормальное распределения непрерывных случайных величин
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл
М(х)= 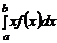 .
.
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения Х принадлежат отрезку [a,b], то
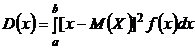 =
= 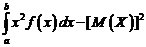 .
.
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной
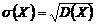 .
.
Пример 4.1. Случайная величина задана плотностью распределения. Найти математическое ожидание и дисперсию.
f(x) = 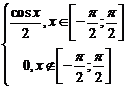
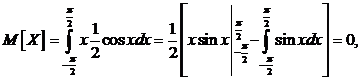
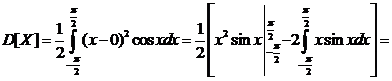
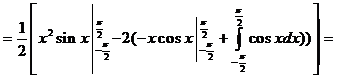
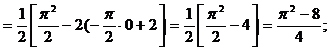
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a,b] , если плотность распределения на этом отрезке постоянна, а вне его равна нулю


 f(x)=
f(x)= 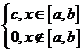

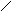


 Из условия
Из условия 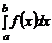 =1 следует
=1 следует
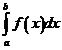 =
= 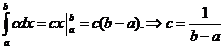

Рис. 5
Вероятность попадания равномерно распределенной случайной величины на интервал (α,β) 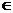 [a,b]:
[a,b]:
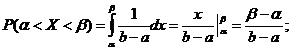
Пример 4.2: Интервал движения автобуса №14 – 15 минут. Случайная величина Х – время ожидания автобуса. Найти вероятность того, что Х 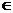 [9,12]
[9,12]
Решение.Найдем искомую вероятность
Р(9 <Х< 12) = 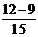
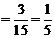 .
.
Построим функцию распределения для закона равномерной плотности. Воспользуемся свойством: F(x)= 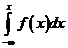 .
.
Тогда: F(x)= 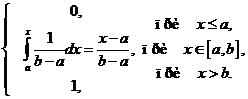
Математическое ожидание и дисперсия равномерного распределения
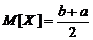 ;
; 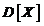
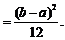
Непрерывная случайная величина Х распределена по показательному закону, если ее плотность вероятности имеет вид:
f(x)= 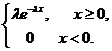
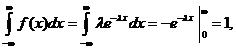
 т.е. условие нормировки выполнено. Найдем математическое ожидание и дисперсию.
т.е. условие нормировки выполнено. Найдем математическое ожидание и дисперсию.
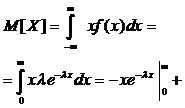
|
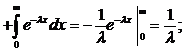
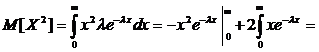
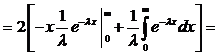
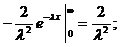
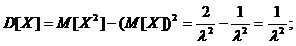
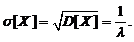
т. о., математическое ожидание и среднеквадратическое отклонение у показательного распределения одинаково.
Пример 4.3. Случайная величина Т – время работы радиолампы имеет показательное распределение. Определить вероятность того, что время работы радиолампы будет не менее 1000 часов, если среднее время ее работы – 500 часов.
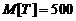 .
. 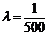 ,
, 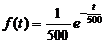 (t>0)
(t>0)
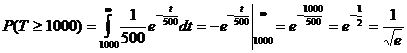
Нормальнымназывают распределение вероятностей непрерывной случайной величины, которое описывается плотностью
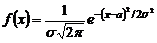 .
.
Здесь 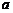 - математическое ожидание,
- математическое ожидание, 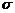 - среднее квадратическое отклонение нормального распределения. Достаточно знать эти два параметра, чтобы задать нормальное распределение. График плотности нормального распределения называют нормальной кривой(кривой Гаусса) (рис. 7, 8). Изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает (рис.7). С возрастанием
- среднее квадратическое отклонение нормального распределения. Достаточно знать эти два параметра, чтобы задать нормальное распределение. График плотности нормального распределения называют нормальной кривой(кривой Гаусса) (рис. 7, 8). Изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает (рис.7). С возрастанием 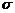 максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох; при убывании
максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох; при убывании 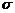 нормальная кривая становится более «островершинной» и растягивается в положи
нормальная кривая становится более «островершинной» и растягивается в положи 
тельном направлении оси Оу (рис. 8).
Вероятность того, что Х примет значение, принадлежащее интервалу 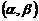
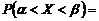 Ф
Ф 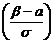 - Ф
- Ф 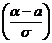 ,
,
где Ф(х) – функция Лапласа, значения которой приведены в таблице.
Пример 4.4. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50).
Решение. По условию, 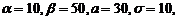 следовательно,
следовательно,
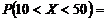 Ф
Ф 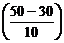 - Ф
- Ф 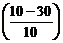 =2Ф(2).
=2Ф(2).
По таблице находим Ф(2)=0,4772. Отсюда, искомая вероятность
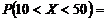
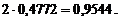
Задачи для самостоятельного решения
1. Случайная величина Х задана в интервале (3,5) плотностью вероятностей f( х) = 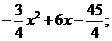 вне этого интервала f(х)=0. Найти математическое ожидание и дисперсию.
вне этого интервала f(х)=0. Найти математическое ожидание и дисперсию.
2.Случайная величина Х задана функцией распределения
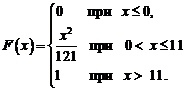 .
.
Требуется найти плотность распределения, математическое ожидание и дисперсию, построить графики функции распределения и плотности вероятности случайной величины Х.
3. Найти вероятность попадания в заданный интервал (α,β) нормально распределенной случайной величины, если известны ее математическое ожидание 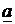 и среднее математическое отклонение σ. α=10, β=50, а=30, σ=10.
и среднее математическое отклонение σ. α=10, β=50, а=30, σ=10.
4. Случайная величина Х задана функцией распределения F(x) = sin2x в интервале (0, 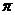 /4). Найти математическое ожидание.
/4). Найти математическое ожидание.
5. Найти дисперсию случайной величины Х, заданной функцией распределенияF(x) = 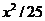 в интервале (0,5).
в интервале (0,5).
6. Случайная величина Х задана плотностью вероятностей f(х) = 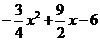 в интервале (2,4), вне этого интервала f(х)=0. Найти математическое ожидание и дисперсию.
в интервале (2,4), вне этого интервала f(х)=0. Найти математическое ожидание и дисперсию.
Ответы. 1. 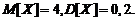 2.
2. 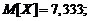
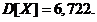 3.
3. 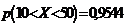 . 4.
. 4. 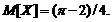 5.
5. 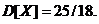 6.
6.