Занятие 2. Числовые характеристики дискретной случайной величины. Функция распределения дискретной случайной величины.
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности..
М (X)= х1р1 + х2р2+ . . . + хп рп.
Пример 2.1.Найти математическое ожидание случайной величины X,зная закон ее распределения:
Х 2 3 5
р 0,30,10,6 .
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:
М(Х)=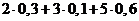 
=3,9.
Рассмотрим свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной величины равно самой постоянно: М(С) = С.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
М (СХ) = СМ (X).
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению ихматематических ожиданий:
М (XY) = М(Х)М(Y).
Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
М (X+Y) = М(Х)+М(Y).
Если величина X распределена по биномиальному закону с параметрами пир, то математическое ожидание равно
М(Х)=пр
Пример 2.2.Вероятность попадания в цель при стрельбе из орудия р=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.
Решение. Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание
М(Х)= пр =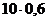 
= 6 (попаданий).
Характеристиками рассеяния возможных значений случайной величины вокруг ее математического ожидания служат дисперсия и среднее квадратическое отклонение..
Отклонением называют разность между случайной величиной и ее математическим ожиданиям.
Приведем важное свойство отклонения.
Математическое ожидание отклонения равно нулю:
М [X - М(Х)]=0.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X)=M[Х-M(X)]2.
Дисперсию удобно вычислять по формуле
D(X)=M(X2)-[M(X)]2.
Пример 2.3. Найти дисперсию случайной величины X,которая задана следующим законом распределения:
| Х | |||
| p | 0,1 | 0,6 | 0,3 |
Решение. Найдем математическое ожидание М (X):
М (X) =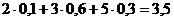 
.
Найдем математическое ожидание М (X2):
М (X2) =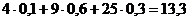 
.
Искомая дисперсия
D(X)=M(X2)-[M(X)]2=13,3-(3,5)2=1,05.
Рассмотрим свойства дисперсии.
Свойство 1.Дисперсия постоянной величины С равна нулю:
D(C)=0.
Это свойство объясняется тем, что постоянная величина сохраняет одно и то же значение и рассеяния не имеет.
Свойство 2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D(СX)=С2 D(X).
Свойство 3.Дисперсия суммы двух независимых случайных величин равна сумме дисперсией этих величин:
D(X+Y)= D(X)+D(Y).
Следствие 1.Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсией этих величин.
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:
Свойство 4.Дисперсия разности двух независимых случайных величин равна сумме их дисперсией:
D(X-Y)= D(X)+D(Y).
Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:
.
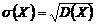Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.
F(x)=Р(Х<x).
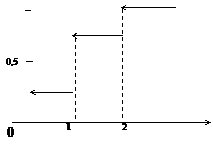
Пример 2.4. Выписать функцию распределения для случайной величины, равной числу выпадений «герба» при бросании двух монет. Изобразить ее график
Решение. Построим ряд распределения (см. пример 1.3)
| X | |||
| P | 0,25 | 0,5 | 0,25 |
Напомним, что по определению F(x)=Р(Х < х). Пусть х < 0. Поскольку наша случайная величина не принимает значений, строго меньших нуля, для рассматриваемого х имеем F(x) = Р(Х < х)= 0. Пусть теперь 0 < х < 1. Для такого х имеем F(x) = Р(Х < х) = 0,25, поскольку X с вероятностью 0,25 может принять 0 . Пусть 1 < х < 2. Для такого х имеем F(x) = Р(Х < х) = .0,25 + 0,5 = 0,75, поскольку X с вероятностью 0,25 может принять значение 0 и с вероятностью 0,5 принять значение 1. Наконец, для х > 2 имеем F(Х) = Р(Х < х) = 1, поскольку с вероятностью 1 случайная величина X принимает одно из значений 0, 1 или 2, и все эти значения лежат в интервале (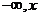 
). Объединим полученные результаты в единую формулу
|
 | |||||
| | |||||
| | |||||
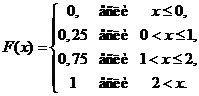
Рис .2.
График функции распределения дискретной случайной величины имеет ступенчатый вид.
Задачи для самостоятельного решения
1.Найти: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение дискретной случайной величины Х по данному закону ее распределения
х  | |||||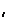
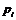 | 0,4 | 0,1 | 0,2 | 0,1 | 0,2 |
2.Пусть дан ряд распределения случайной величины Х:
| х | ||||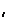
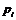| | 0,064 | 0,288 | 0,432 | 0,216 |
Построить функцию распределения.
3. Случайная величина Х задана законом распределения
| х | ||||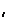
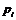| | 0,1 | 0,15 | 0,25 | 0,5 |
Найти и построить функцию распределения, математическое ожидание и дисперсию
4. Случайная величина Х задана законом распределения
| х 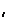| -1 | |||
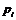| | 0,2 | 0,3 | 0,3 | 0,2 |
Найти дисперсию
5. Дана функция распределения дискретной случайной величины
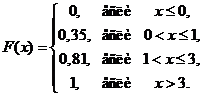
Построить по этой функции ряд распределения.
Ответы: 1. М(Х)= 5,5; D(X) =7,05;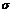 
=2,655. 3. М(Х)= 3,25,D(X) =39,4875. 4. D(X) =14,41.