Общие указания по выполнению расчетно-графических работ
Н. Б. ЛЕВЧЕНКО
Л. М. КАГАН-РОЗЕНЦВЕЙГ
И. А. КУПРИЯНОВ
О. Б. ХАЛЕЦКАЯ
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ЧАСТЬ 1
Санкт-Петербург
Министерство образования и науки Российской Федерации
Санкт-Петербургский государственный архитектурно-строительный
университет
Автомобильно-дорожный факультет
Кафедра сопротивления материалов
Н. Б. ЛЕВЧЕНКО
Л. М. КАГАН-РОЗЕНЦВЕЙГ
И. А. КУПРИЯНОВ
О. Б. ХАЛЕЦКАЯ
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Учебное пособие по выполнению расчетно-графических
работ для студентов всех специальностей и форм обучения
ЧАСТЬ 1
Задачи № 1–11
Под редакцией д-ра техн. наук, проф. В. Д. Харлаба
Санкт-Петербург
УДК 539.3/8(07)
Сопротивление материалов:Учебное пособие по выполнению расчетно-графических работ для студентов всех специальностей и форм обучения. Ч. 1 / Н. Б. Левченко (гл. 1, кроме разд. 1.2.3), Л. М. Каган-Розенцвейг (гл. 2), И. А. Куприянов (гл. 1, разд. 1.2.3; гл. 3), О. Б. Халецкая (гл. 2); СПбГАСУ. СПб., 2001. с.
В пособии даны краткие сведения из теории, необходимые для решения задач, и приводятся примеры решения задач, входящих в расчетно-графические работы, по трем темам: "Растяжение-сжатие", "Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного состояния" и "Кручение". Решение задач снабжено подробными объяснениями.
Ил. 54. Библиогр. 4 назв.
Рецензенты:
д-р техн. наук, проф. В. З. Васильев (Санкт-Петербургский государственный университет путей сообщения);
д-р техн. наук, проф. В. В. Улитин (Санкт-Петербургский государственный университет низкотемпературных и пищевых технологий)
Рекомендовано Редакционно-издательским советом СПбГАСУ в качестве учебного пособия
© Н. Б. Левченко, Л. М. Каган-Розенцвейг,
И. А. Куприянов, О. Б. Халецкая, 2011
© Санкт-Петербургский государственный
архитектурно-строительный университет, 2011
ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
В процессе изучения курса "Сопротивление материалов" студенты выполняют расчетно-графические работы (РГР). Количество РГР и задач, входящих в каждую из этих работ, зависит от специальности и количества часов, отведенных в учебном плане на изучение курса. Цель РГР – сознательное усвоение теоретического курса и приобретение навыков решения задач, имеющих как академический, так и практический характер.
Данное учебное пособие предназначено для оказания помощи студентам при выполнении расчетно-графических работ. Номера задач, решение которых объясняется в данном пособии, соответствуют номерам задач в издании [4], по которому студенты выбирают схемы решаемых задач.
В данном пособии приводятся краткие теоретические сведения и основные формулы, необходимые для выполнения задач, объясняются смысл и порядок решения задач. Решение одних задач сопровождается численными расчетами, решение других приведено в общем виде. Ни в коем случае не следует копировать решение задач, не разобравшись со смыслом того, что Вы делаете. Пособие не заменяет учебник, поэтому перед выполнением задач прочитайте те разделы учебников, которые приведены в перечне литературы по изучаемой теме. В процессе расчетов обращайте внимание на единицы измерения величин, входящих в формулы. Не забывайте писать, в каких единицах Вы получили результат. Рекомендуемые единицы измерения приведены в перечне используемых обозначений. Все арифметические вычисления следует выполнять с точностью до трех значащих цифр – точностью, достаточной для инженерных расчетов.
Расчетно-графические работы оформляются на одной стороне стандартных листов писчей бумаги формата А-4 (210х297). Перед решением задачи необходимо нарисовать расчетную схему задачи в масштабе в соответствии со своими данными. Решение задачи должно сопровождаться короткими пояснениями, рисунки желательно делать карандашом, на листах должны быть оставлены поля для замечаний преподавателя. После выполнения всех задач, входящих в расчетно-графическую работу, листы с решением следует сброшюровать и снабдить титульным листом.
ИСПОЛЬЗУЕМЫЕ ОБОЗНАЧЕНИЯ
Нагрузки:
 – сосредоточенная сила, кН;
– сосредоточенная сила, кН; 
 – сосредоточенная пара сил (момент), кН×м;
– сосредоточенная пара сил (момент), кН×м;
 – интенсивность распределенной по длине стержня нагрузки, кН/м.
– интенсивность распределенной по длине стержня нагрузки, кН/м.
Обозначение осей:
 – продольная ось стержня;
– продольная ось стержня;
 – главные центральные оси инерции поперечного сечения стержня.
– главные центральные оси инерции поперечного сечения стержня.
Геометрические характеристики поперечного сечения стержня:
 – площадь поперечного сечения, см2;
– площадь поперечного сечения, см2;
 – статические моменты относительно осей
– статические моменты относительно осей  ,
,  см3;
см3; 
 – осевые моменты инерции относительно осей
– осевые моменты инерции относительно осей  , см4;
, см4;
 – полярный момент инерции, см4.
– полярный момент инерции, см4.
Внутренние усилия:
N – продольная сила, кН;
Qy , Qz , (Q)– поперечные силы, кН;
My , Mz, (M)– изгибающие моменты кН×м;
Mк – крутящий момент, кН×м.
Напряжения:
 (s) – нормальные напряжения, МПа;
(s) – нормальные напряжения, МПа;
 (t) – касательные напряжения, МПа;
(t) – касательные напряжения, МПа;
 (sгл) – главные напряжения, МПа.
(sгл) – главные напряжения, МПа.
Деформации и перемещения:
 ,(e) – относительные линейные деформации;
,(e) – относительные линейные деформации;
 (g) – угловые деформации (углы сдвига);
(g) – угловые деформации (углы сдвига);
 – абсолютная деформация стержня при растяжении-сжатии (переме-
– абсолютная деформация стержня при растяжении-сжатии (переме-
щения точек оси вдоль оси x), см;
v, w – прогибы оси стержня (балки) при изгибе (перемещения точек оси вдоль осей y, z), см;
j – угол поворота оси стержня (балки) при изгибе, рад;
q – угол закручивания стержня (вала) при кручении, рад.
Характеристики материала:
sпц – предел пропорциональности, МПа;
sт – предел текучести, МПа;
sв – временное сопротивление (для хрупких материалов  – предел прочности при растяжении,
– предел прочности при растяжении,  – предел прочности при сжатии), МПа;
– предел прочности при сжатии), МПа;
[s], [t] – допускаемые напряжения, МПа; 

E – модуль упругости, МПа;
n – коэффициент Пуассона;
 – коэффициент линейного температурного расширения, 1/град.
– коэффициент линейного температурного расширения, 1/град.
РАСТЯЖЕНИЕ-СЖАТИЕ
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.1, 2.2), гл. 3 (§ 3.1, 3.4, 3.6–3.12).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 2.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 1 (§ 1.3), гл. 2.
Основные понятия и формулы
Растяжение-сжатие – простейший вид деформации стержня. При растяжении-сжатии в стержне из шести видов внутренних усилий возникает только одно усилие – продольная сила N.
 Рис.1.1. Правило знаков для продольной силы Рис.1.1. Правило знаков для продольной силы |
Для определения внутренних усилий в стержнях и стержневых системах используется метод сечений. Согласно этому методу из уравнения равновесия отсеченной части стержня следует, что продольная сила – внутреннее усилие, численно равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 1.1). Часто внутреннее усилие меняется по длине стержня, в этом случае принято рисовать график изменения усилия вдоль оси стержня, который называется эпюрой. Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти  при растяжении-сжатии). Сечение, где действует максимальное усилие, будем называть опасным.
при растяжении-сжатии). Сечение, где действует максимальное усилие, будем называть опасным.
После определения продольной силы можно найти нормальное напряжение в поперечном сечении стержня при растяжении-сжатии по формуле
 Рис. 1.2. Деформация растянутого стержня Рис. 1.2. Деформация растянутого стержня |
 . (1.1)
. (1.1)
Абсолютная деформация стержня (его удлинение или укорочение) в том случае, если материал стержня работает упруго, т. е. подчиняется закону Гука, определяется так:
 (1.2)
(1.2)
На рис. 1.2 показано удлинение стержня Dl, загруженного силой F.Если не учитывать собственный вес, то продольная сила не меняется по длине стержня (для стержня, показанного на рис. 1.2,  ) и
) и  , то
, то
 . (1.3)
. (1.3)
Если задача решается с учетом собственного веса, т. е. усилие N линейно зависит от х, то из (1.2) при  можно получить формулу
можно получить формулу
 , (1.4)
, (1.4)
где  – собственный вес стержня; g – объемный вес материала.
– собственный вес стержня; g – объемный вес материала.
Примеры решения задач
Условие задачи
Стержень переменного сечения с заданным отношением площадей 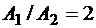 подвержен действию нагрузок, показанных на рис. 1.3, а. Цель расчета – подобрать площади поперечного сечения стержня так, чтобы на каждом участке соблюдалось условие прочности (1.5) или (1.7). (При этом должно выполняться заданное отношение площадей.)
подвержен действию нагрузок, показанных на рис. 1.3, а. Цель расчета – подобрать площади поперечного сечения стержня так, чтобы на каждом участке соблюдалось условие прочности (1.5) или (1.7). (При этом должно выполняться заданное отношение площадей.)
Решение
Определяем продольную силу и строим эпюру распределения N вдоль оси стержня. Для этого сначала из уравнения равновесия всего стержня находим опорную реакцию:
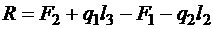 .
. 
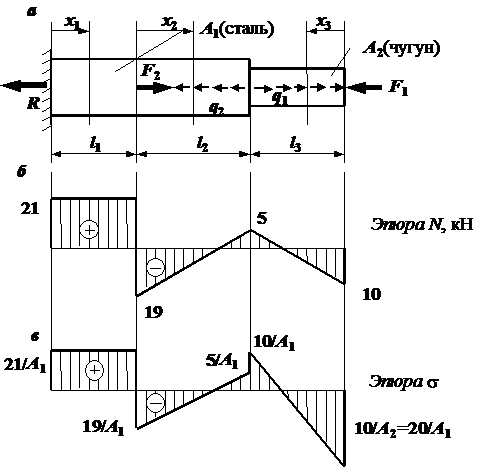 Рис. 1.3. К решению задачи № 1: а – схема нагрузки на стержень; б, в – эпюры продольной силы и напряжений Рис. 1.3. К решению задачи № 1: а – схема нагрузки на стержень; б, в – эпюры продольной силы и напряжений |
Затем, используя метод сечений, определяем продольную силу в произвольном сечении на каждом участке стержня:
на первом участке 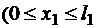 )
) 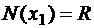 ;
;
на втором участке 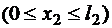
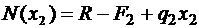 ;
;
на третьем участке 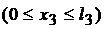
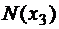
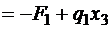 .
.
Поясним, что на первом и втором участках суммируем все силы, находящиеся слева от рассматриваемого сечения, на третьем участке в выражение для продольной силы входят силы, расположенные справа от сечения.
Ищем значения N на границах участков. На первом участке продольная сила постоянна и не зависит от x. В начале второго участка
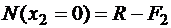 ,
,
в конце второго участка
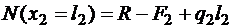 .
.
Аналогично для третьего участка
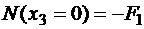 ,
, 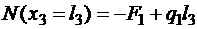 .
.
По полученным точкам строим эпюру N. На рис. 1.3, б эпюра N построена для следующих исходных данных: 
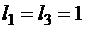 м,
м, 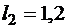 м; F1 = 10 кН, F2 = 40 кН, q1 = 15 кН/м, q2 = 20 кН/м.
м; F1 = 10 кН, F2 = 40 кН, q1 = 15 кН/м, q2 = 20 кН/м.
Зная продольную силу, по формуле (1.1) находим напряжения в стержне и строим эпюру распределения напряжений по длине стержня (рис. 1.3, в). Для этого площади сечений на всех участках выразим, используя заданное отношение площадей, через одну неизвестную величину 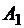 . Заметим, что на эпюре продольных сил скачки (т. е. резкие изменения усилий при переходе в соседнее сечение) имеют место под сосредоточенными силами на величину этих сил, на эпюре напряжений скачки появляются также и в местах изменения поперечного сечения.
. Заметим, что на эпюре продольных сил скачки (т. е. резкие изменения усилий при переходе в соседнее сечение) имеют место под сосредоточенными силами на величину этих сил, на эпюре напряжений скачки появляются также и в местах изменения поперечного сечения.
Для подбора сечения стержня по эпюре напряжений выбираем опасные сечения с максимальными напряжениями. Причем для хрупких материалов важным является не только абсолютное значение напряжения, но и его знак. Более опасным является растягивающее напряжение, так как разрушающее напряжение при растяжении у хрупкого материала много меньше прочности при сжатии. Например, на эпюре 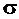 , показанной на рис. 1.3, в, опасным является не только сечение в начале третьего участка
, показанной на рис. 1.3, в, опасным является не только сечение в начале третьего участка 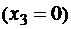 , где действуют максимальные сжимающие напряжения, но и сечение в конце третьего участка
, где действуют максимальные сжимающие напряжения, но и сечение в конце третьего участка 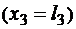 с максимальными растягивающими напряжениями. Таким образом, для стержня, показанного на рис. 1.3, должны выполняться условия прочности в трех опасных сечениях:
с максимальными растягивающими напряжениями. Таким образом, для стержня, показанного на рис. 1.3, должны выполняться условия прочности в трех опасных сечениях:
для чугунной части
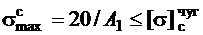 , откуда
, откуда 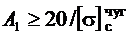 ,
,
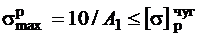 и
и 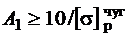 ;
;
для стальной части
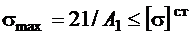 , тогда
, тогда 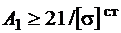 .
.
Из трех значений A1, найденных из условий прочности в опасных сечениях выбираем то, которое удовлетворяет всем условиям (то есть максимальное их всех найденных значение 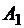 . Величину А2 находим по заданному соотношению:
. Величину А2 находим по заданному соотношению: 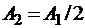 .
.
Для проверки вычислений находим действительные коэффициенты запаса прочности на каждом участке по формуле (1.8) и сравниваем их с нормируемым коэффициентом запаса. На самом опасном участке (в опасном сечении) действительный коэффициент запаса прочности должен равняться нормируемому, а на остальных участках согласно (1.7) должен быть больше нормируемого.
Условие задачи
Стержень переменного сечения с соотношением площадей поперечных сечений A1/A2 = 2 находится под действием сосредоточенных сил и собственного веса (рис. 1.4, а). Материал стержня на всех участках одинаков. Требуется построить эпюры распределения продольной силы и напряжений вдоль оси стержня и определить перемещение сечения а–а.
Решение
Строим эпюры изменения продольной силы и напряжений вдоль оси стержня. Собственный вес стержня принято учитывать, заменяя его распределенной по всей длине нагрузкой. Интенсивность распределенной нагрузки равна собственному весу, действующему на единицу длины стержня, т. е.
на первом и втором участках
 ,
,
на третьем участке
 ,
,
 Рис. 1.4. К решению задачи № 2: а – схема нагрузки на стержень; б, в – эпюры продольной силы и напряжений Рис. 1.4. К решению задачи № 2: а – схема нагрузки на стержень; б, в – эпюры продольной силы и напряжений |
где g – объемный вес материала стержня.
Эпюры продольной силы и напряжений строим, используя метод сечений, аналогично тому, как это делали в задаче № 1. Заметим, что угол наклона эпюры продольной силы зависит от величины q и, следовательно, при построении эпюры N в масштабе угол ее наклона на первом и втором участке должен быть больше, чем на третьем участке, так как A1 по условию больше, чем A2 (рис. 1.4, б). Угол же наклона эпюры напряжений зависит от объемного веса g, и поэтому угол наклона эпюры напряжений на всех участках одинаков (рис. 1.4, в).
Находим перемещение (опускание) сечения а–а. Это перемещение можно искать разными способами. По первому способу для определения перемещения используем формулу (1.4). Здесь F – сосредоточенная сила, вызывающая перемещение участка длиной l; G – собственный вес рассматриваемого участка. Эту формулу можно использовать на участках постоянного сечения между сосредоточенными силами. Отсчет надо вести от неподвижного сечения, т. е. заделки. Например, в рассматриваемой задаче перемещение сечения а–а складывается из удлинения участка длиной l1, которое мы обозначим Dl1, и удлинения участка длиной la – Dla. При определении удлинения Dl1 в формуле (1.4) сила F равна сумме F1, F2 и собственного веса всех расположенных ниже участков. Вес рассматриваемого участка стержня длиной l1:  . Таким образом, по (1.4)
. Таким образом, по (1.4)
 .
.
Удлинение Dla происходит под действием сосредоточенной силы, состоящей из силы F2, веса участков стержня, расположенных ниже сечения а–а, и собственного веса участка  . То есть
. То есть
 .
.
Окончательно опускание сечения а–а равно  .
.
Если построена эпюра распределения напряжений, то для определения перемещения заданного сечения удобно использовать второй способ, применяя формулу (1.2). В формуле (1.2)  , а
, а  – это площадь эпюры напряжений на участке между неподвижным сечением (заделкой) и рассматриваемым сечением а-а. Таким образом, если найти площадь двух трапеций на указанном участке (заштрихованные площади
– это площадь эпюры напряжений на участке между неподвижным сечением (заделкой) и рассматриваемым сечением а-а. Таким образом, если найти площадь двух трапеций на указанном участке (заштрихованные площади  и
и  эпюры s на рис. 1.4, в)и разделить полученную величину на модуль упругости, мы получим искомое перемещение сечения а–а:
эпюры s на рис. 1.4, в)и разделить полученную величину на модуль упругости, мы получим искомое перемещение сечения а–а:
 .
.
При вычислении перемещения обращайте внимание на единицы измерения величин, входящих в формулы. Рекомендуем окончательный результат получить в сантиметрах.
Условие задачи
Конструкция, состоящая из стержней, соединенных шарнирами, загружена силой F (рис. 1.5). Сечения стержней – из прокатных профилей, площади сечений можно найти по сортаментам стального проката (например, в [1]). Цель расчета:
1) определить значение допускаемой нагрузки;
2) найти перемещение узла С.
 Рис. 1.5. Схема конструкции в задаче № 3 Рис. 1.5. Схема конструкции в задаче № 3 |
Примечание. Если на схеме, выбранной студентом по [4], один стержень показан более жирным, то его следует считать абсолютно жестким, т. е. деформациями этого стержня нужно пренебречь.
Решение
 Рис. 1.6. План сил Рис. 1.6. План сил |
Для определения усилий используем метод сечений. Для этого нарисуем план сил: рассечем деформируемые стержни конструкции и отброшенные части стержней заменим продольными силами N1 и N2 (рис. 1.6). Найдем усилия N1 и N2 из уравнений равновесия отсеченной части конструкции. Желательно составлять такие уравнения равновесия, чтобы в каждое уравнение входило только одно неизвестное усилие, например, 
 для определения N1 и
для определения N1 и  (рис. 1.6) для нахождения N2..[1]. Эти уравнения в рассматриваемой задаче имеют вид:
(рис. 1.6) для нахождения N2..[1]. Эти уравнения в рассматриваемой задаче имеют вид:
 и
и  . Откуда
. Откуда
 и
и  .
.
Знак минус показывает, что направление усилия в стержне 2 противоположно показанному на рис. 1.6, т. е. стержень 2 сжат.
Определим напряжения по (1.1) и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче это будет стержень 1).
Из условия прочности этого стержня получим значение допускаемой нагрузки:
 ,
,  .
.
Найдем перемещение узла С, построив план перемещений (рис. 1.7). Предварительно найдем абсолютные деформации стержней Dl1и Dl2 по формуле (1.3). В рассматриваемой задаче растянутый стержень 1 будет удлиняться, а сжатый стержень 2 – укорачиваться. Для построения плана перемещений нарисуем схему конструкции в масштабе и отложим отрезки Dl1 и Dl2 вдоль оси каждого стержня, выбрав масштаб для деформаций так, чтобы картинка плана перемещений была наглядной. В процессе деформации стержни поворачиваются относительно точек А и В по дугам. Из-за малости деформаций эти дуги заменяем касательными, т. е. перпендикулярами к направлениям стержней (отрезки  и
и  на рис. 1.7). На пересечении дуг (перпендикуляров к направлениям стержней) находится новое положение узла C после деформации – точка
на рис. 1.7). На пересечении дуг (перпендикуляров к направлениям стержней) находится новое положение узла C после деформации – точка 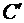 на рис. 1.7. Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных геометрических выкладок.
на рис. 1.7. Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных геометрических выкладок.
 Рис. 1.7. План перемещений Рис. 1.7. План перемещений |
Примечание. Если конструкция имеет абсолютно жесткий стержень, то принцип построения плана перемещений тот же. Все точки абсолютно жесткого стержня могут перемещаться только по дугам (перпендикулярам к направлению стержня), поворачиваясь вокруг неподвижного шарнира. Например, если стержень АС на рис. 1.7 считать абсолютно жестким, то точка С переместится в положение  и горизонтальное перемещение узла С будет равно нулю.
и горизонтальное перемещение узла С будет равно нулю.
СТЕРЖНЕВЫХ СИСТЕМ
Основные определения
Статически неопределимая система – система, в которой количество неизвестных (опорных реакций, внутренних усилий) больше числа независимых уравнений статики, составляемых для рассматриваемой системы (конструкции). Таким образом, в статически неопределимой системе невозможно найти все неизвестные, пользуясь только уравнениями равновесия. Разность между количеством неизвестных и числом независимых уравнений статики называется степенью статической неопределимости.
Конструкции, состоящие из стержней, соединенных шарнирами, называются шарнирно-стержневыми. В этих конструкциях есть стержни, которые обеспечивают геометрическую неизменяемость конструкции и при удалении которых система превращается в механизм. Такие стержни будем называть необходимыми. Если же при удалении некоторых стержней геометрическая неизменяемость конструкции не нарушается, то такие стержни назовем лишними. В статически определимой системе есть только необходимые стержни, в статически неопределимой – число лишних стержней равно степени статической неопределимости.
Порядок определения всех неизвестных в статически неопределимых конструкциях (раскрытия статической неопределимости) следующий:
1) записываем необходимые для определения внутренних усилий и опорных реакций уравнения равновесия;
2) составляем уравнения совместности деформаций (геометри-ческие уравнения). Количество уравнений совместности деформаций равно степени статической неопределимости;
3) записываем физические уравнения, связывающие усилия и деформации;
4) решая полученную систему уравнений, находим все неизвестные.
Если в качестве физических уравнений используется закон Гука, то такой способ расчета носит название расчета по упругой стадии деформаций.После определения внутренних усилий – продольных сил в стержнях статически неопределимой системы – встает задача обеспечения ее прочности. При расчете по упругой стадии деформаций считается, что предельное состояние конструкции наступает тогда, когда один, наиболее напряженный, стержень переходит в предельное состояние (разрушится или потечет). Поэтому после определения усилий по этому способу находим напряжения в стержнях и выбираем стержень, в котором действует максимальное напряжение. Из условия прочности этого наиболее напряженного стержня либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней. Следует отметить, что в большинстве статически неопределимых конструкций в результате расчета по этому способу только в одном стержне напряжения будут равны допускаемым, остальные же стержни будут недогружены. Достичь равенства напряжений во всех элементах конструкции и, следовательно, добиться выполнения требования, чтобы напряжения во всех стержнях равнялись допускаемым, в общем случае невозможно.
Второй способ расчета статически неопределимых стержневых систем носит название расчетапо предельному пластическому состоянию.[2] Благодаря наличию лишних стержней в статически неопределимой системе, наступление состояния текучести в одном (наиболее напряженном) стержне еще не приводит к нарушению геометрической неизменяемости всей конструкции. Остальные стержни, оставаясь упругими, препятствуют пластическим деформациям этого стержня. Конструкция продолжает выполнять свое назначение, перейдя из упругой стадии работы в упругопластическую. При увеличении нагрузки в пластическую стадию работы вовлекаются все новые стержни. И только тогда, когда в системе потекут все лишние стержни и хотя бы один необходимый, конструкция превращается в механизм и не может выполнять свои функции. Это состояние и считается предельным при расчете по предельному пластическому состоянию. Таким образом, расчет по предельному пластическому состоянию сводится к следующему:
1) определяем, сколько стержней должно потечь, чтобы конструкция превратилась в механизм. Дальнейший расчет возможен по двум вариантам:
· если в предельном состоянии текут все стержни системы, то, составляя уравнения равновесия конструкции в предельном состоянии, находим из него значение предельной нагрузки  ;
;
· если в предельном состоянии течет только часть стержней, то, не определяя порядка перехода стержней в пластическое состояние, рассматриваем все кинематически возможные варианты предельного состояния конструкции. Находим из уравнений равновесия предельную нагрузку для каждого варианта. Выбираем из всех вариантов минимальное значение предельной нагрузки  ;
;
2) из условия прочности конструкции по предельному состоянию  либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней.
либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней.
Отметим, что расчет по предельному пластическому состоянию является более экономичным, чем расчет по упругой стадии деформаций. Поэтому при сравнении результатов расчета по двум способам должно получиться, что допускаемая нагрузка, найденная расчетом по предельному пластическому состоянию, всегда не меньше нагрузки, полученной расчетом по упругой стадии деформации. Соответственно площади сечений стержней, найденные расчетом по предельному состоянию, должны быть не больше площадей сечений, полученных расчетом по упругой стадии деформаций.
Примеры решения задач
Условие задачи
 Рис. 1.8. Схема нагрузки на стержень в задаче № 4 Рис. 1.8. Схема нагрузки на стержень в задаче № 4 |
Стержень переменного сечения с заданным соотношением площадей поперечного сечения 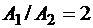 , выполненный из разного материала, загружен силой F (рис. 1.8). Между правым концом стержня и стенкой существует зазор
, выполненный из разного материала, загружен силой F (рис. 1.8). Между правым концом стержня и стенкой существует зазор 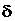 .
.
Требуется:
1) определить продольные силы, напряжения на каждом участке и проверить прочность стержня от действия заданной нагрузки F.
2) найти дополнительные напряжения, возникающие в стержне при его нагревании на температуру 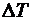 и проверить прочность стержня от температурного воздействия.
и проверить прочность стержня от температурного воздействия.
Решение
I. Определение напряжений от заданной нагрузки
Прежде всего, надо убедиться, что заданная система является статически неопределимой. Найдем абсолютную деформацию стержня, показанного на рис. 1.8, предполагая сначала, что правая стенка отсутствует. Тогда, используя метод сечений, определим продольные силы на трех участках стержня:
на первом участке длиной 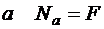 ;
;
на втором и третьем участках 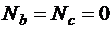 .
.
Полное удлинение стержня, равное в общем случае 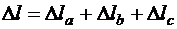 , в данной задаче равно удлинению первого участка и, следовательно, по (1.3)
, в данной задаче равно удлинению первого участка и, следовательно, по (1.3)
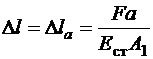 .
.
Если под действием нагрузки абсолютная деформация 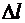 стержня будет больше заданного зазора
стержня будет больше заданного зазора  , то стержень упрется правым концом в стенку и возникнут опорные реакции как в левом защемлении (
, то стержень упрется правым концом в стенку и возникнут опорные реакции как в левом защемлении ( 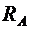 ), так и в правом опорном закреплении (
), так и в правом опорном закреплении ( 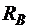 ) (рис. 1.9, а). Для заданной системы можно составить только одно независимое уравнение статики
) (рис. 1.9, а). Для заданной системы можно составить только одно независимое уравнение статики 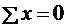 . Таким образом, две неизвестные опорные реакции нельзя найти из одного уравнения, и система в процессе деформации становится один раз статически неопределимой.
. Таким образом, две неизвестные опорные реакции нельзя найти из одного уравнения, и система в процессе деформации становится один раз статически неопределимой.
Для раскрытия статической неопределимости используем расчет по упругой стадии деформаций и запишем три группы уравнений:
1) уравнения равновесия. Из них получим:
· для всего стержня 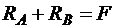 ;
;
· для отсеченных частей стержня 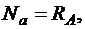
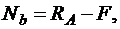
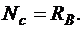 Заметим, что при составлении уравнений равновесия отсеченных частей стержня сделано предположение, что первая и вторая части стержня растянуты, а третья часть – сжата;
Заметим, что при составлении уравнений равновесия отсеченных частей стержня сделано предположение, что первая и вторая части стержня растянуты, а третья часть – сжата;
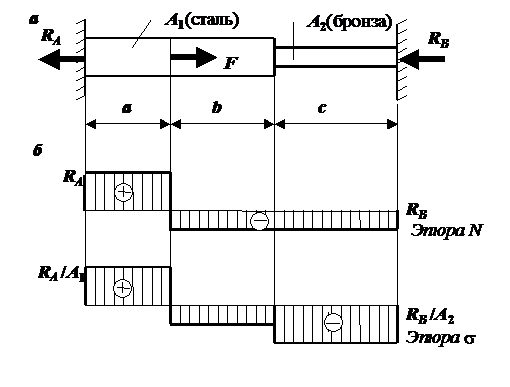 Рис. 1.9. К решению задачи № 4: а – план сил от действия F, б – эпюры продольной силы и напряжений от F Рис. 1.9. К решению задачи № 4: а – план сил от действия F, б – эпюры продольной силы и напряжений от F |
2) уравнение совместности деформаций, смысл которого в данной задаче очень простой: полная деформация стержня равна заданному зазору. При составлении уравнения совместности деформаций важно, чтобы знаки абсолютных деформаций соответствовали сделанным предположениям о направлении усилий. В нашем примере 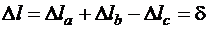 ;
;
3) физические уравнения
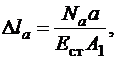
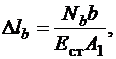
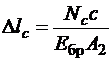 .
.
Решив полученную систему уравнений, найдем продольные силы, а затем напряжения в разных частях стержня и построим эпюры их распределения по длине стержня (рис. 1.9, б). Если знак усилия после решения системы уравнений получился отрицательным, это означает, что сделанное предположение о направлении продольной силы не подтвердилось. В рассмотренной задаче отрицательным должно получиться усилие 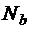 , т. е. второй участок длиной b не растянут, а сжат. Знаки N и s на эпюрах ставим в соответствии с правилом знаков для продольной силы.
, т. е. второй участок длиной b не растянут, а сжат. Знаки N и s на эпюрах ставим в соответствии с правилом знаков для продольной силы.
После определения напряжений производим проверку прочности по формулам (1.5) или (1.7) так же, как в статически определимой системе. Если условие прочности на каком-нибудь участке стержня не будет выполняться, измените значение F так, чтобы условие прочности соблюдалось.
II.Определение температурных напряжений
Найдем удлинение стержня от температурного воздействия 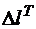 и убедимся в том, что это удлинение больше заданного зазора
и убедимся в том, что это удлинение больше заданного зазора  .
.
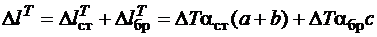 .
.
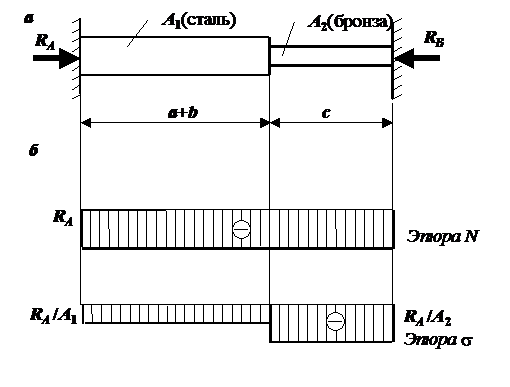 Рис. 1.10. К решению задачи № 4: а – план сил от действия Рис. 1.10. К решению задачи № 4: а – план сил от действия 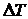 , б – эпюры продольной силы и напряжений от , б – эпюры продольной силы и напряжений от 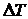 |
Если 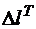 >
>  , то система является один раз статически неопределимой, и раскрытие статической неопределимости производим по той же схеме, что и в предыдущей части задачи:
, то система является один раз статически неопределимой, и раскрытие статической неопределимости производим по той же схеме, что и в предыдущей части задачи:
Из уравнений равновесия следует, что 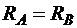 и
и 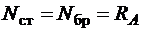 . Здесь в соответствии с рис. 1.10, а предполагаем, что стержень всюду сжат. (Силу F при определении температурных напряжений считаем равной нулю.)
. Здесь в соответствии с рис. 1.10, а предполагаем, что стержень всюду сжат. (Силу F при определении температурных напряжений считаем равной нулю.)
Уравнение совместности деформации показывает, что абсолютная деформация стержня, равная разности удлинения стержня от температурного воздействия 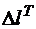 и укорочения от действия сжимающих продольных сил
и укорочения от действия сжимающих продольных сил 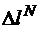 не может быть больше заданного зазора
не может быть больше заданного зазора  :
:
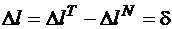 ,
,
где 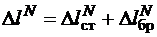 .
.
Укорочение стержня от действия продольных сил найдем, используя физические уравнения (закон Гука):
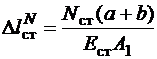 и
и 

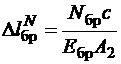 .
.
После решения полученной системы уравнений найдем усилия в обеих частях стержня. Полученный положительный знак должен подтвердить предположение о том, что стержень сжат. Строим эпюры продольной силы и напряжений (рис. 1.10, б) от температурного воздействия.
Проверяем прочность стержня и в случае невыполнения условия прочности на каком-нибудь участке находим новое значение 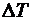 , при котором условие прочности будет соблюдаться на всех участках.
, при котором условие прочности будет соблюдаться на всех участках.
Условие задачи
Стержневая конструкция, состоящая из абсолютно жесткого диска и двух деформируемых стержней длиной l1 и l2, соединенных шарнирами, подвержена действию силы F (рис. 1.11). Примем следующие исходные данн
