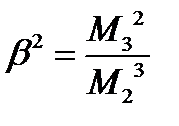Центральная предельная теорема. Закон больших чисел.

Под законом больших чисел в теории вероятности понимается ряд теорем в каждой из которых устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным. В основе лежит неравенство Чебышева (Пафнутий)

Теорема.

Неравенство Чебышева. Пусть имеется СВ Х с математическим ожиданием m и дисперсией Д, каково бы нибыло положительное число Е вероятностью того, что величина Х отклонится от своего математического ожидания не менее чем на Е ограничено сверху числом Д/ Е^2. P(|x-m|>=E)<=Д/Е^2, еще можно записать в эквивалентной форме если перейти от события |x-m|>=E к противоположенному событию |x-m|<E , то тогда

P(|x-m|<E)> 1-Е^2

Теорема. Пусть имеется бесконечная последовательность Х1, Х2… независимых случайных величин с одним и тем же математическим ожиданиемm и дисперсией с ограниченным числом C тогда каково бы ни было положительное число Е вероятность события |((x1+x2+…xn)/n)-m|<E стремится к 1 при n -> бесконечн. Тем самым оправдывается рекомендуемый в практической деятельности метод получения более точных результатов, измерений т.е. берется среднее арифметическое большого числа измерений.

Центральная предельная теорема:

Величина Sn=(X1+X2+…Xn)/n случайная, а значит имеет некоторый закон распределения. Распределение суммы большого числа независимых случайных величин при весьма общих условий близка к нормальному распределению.

Есть еще теорема в форме Ляпунова.

ВОПРОС № 14.

Генеральная совокупность и выборка. Вариационный ряд. Гистограмма и полигон частот. Эмпирическая функция распределения.

Генеральной совокупностью называют совокупность объектов из которых производится выборкой.

Выборкой называют совокупность случайно отобранных объектов.

Если выборка правильно отражает соотношение в генеральной совокупности то ее называют репрезентативной ( представительной)

Объемом совокупности называют число ее объектов. Выборка представляет собой ряд чисел являющимися характеристиками исследуемых объектов. Вариационный ряд Х*₁ Х*₂ ….Х*_n представляет собой ту же самую выборку но расположены в порядке неубывания элементов:

Х*₁ <= Х*₂ <=…<= Х*_n

Значение случайной величины соответствующие отдельной группе сгруппированного ряда наблюдаемых данных называется вариантой (Хi)

Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотой вариантой (ni)

Σ_ni =n

Отношение частоты данной варианты к объему выборки называется относительной частотой данной варианты. Р*_i = n_i/n

Дискретным вариационным рядом называется ранжированная ( в порядке неубывания) совокупность вариант X_i c соответствующим им частотами или относительными частотами.

Интервальным вариационным рядом называется упорядоченная последовательность интервалов варьирования случайной величины с соответствующими частотами или относительными частотами попаданий в каждой из них значений случайной величины. Для наглядности наблюдаемые данные изображают графически. Интервальный вариационный ряд графически изображается с помощью гистограммы. Для ее построения в прямоугольной системе координат на оси Х откладываются интервалы варьирования, а на оси У частоты или относительной частоты.

Вариационный ряд дискретной случайной величины графически представляет в виде полигона распределение частот или относительных частот, для этого в прямоугольной системе координат строятся точки с координатами (Хi; ni) затем последовательно соединяются ломанными линиями, которые называются полигонами.

Эмпирическая функция распределения случайной величины Х называют функцию относительной частоты числа наблюдений n_х

F*(x)=n_x/n, где n_x/n – относительная частота события где Х<х. Эта функция служит для приближенного представления о теоретической функции распределения. График эмпирической функции называют графиком накопленных частот.

Функция дискретной случайной величины. Начальные моменты. Основные распределения дискретной случайной величины.

О. Функция распределения для дискретной случайной величины X, которая может принимать значения x1, x2 … xn с соответствующими вероятностями имеет вид:

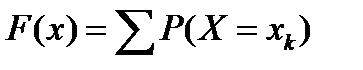
Суммируются вероятности тех значений, которые меньше x.

Пример

X
P	0,2	0,4	0,3	0,1

Дискретная случайная величина x делит бесконечную прямую на промежутки:

X	(-∞;0]	(0;1]	(1;2]	(2;3]	(3;+∞]
P		0,2	0,6	0,9

Начальные и центральные моменты

Начальные и центральным момента k случайной величины X считается математическое ожидание величины X в степени k:

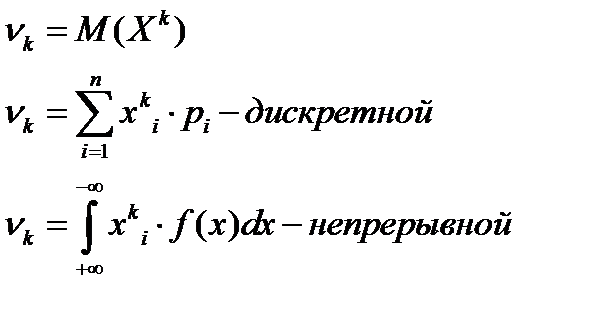
Начальный момент равен математическому ожиданию случайной величины X V1=M(X)

Центральным моментом порядка k случайной величины X называется математическое ожидание величины (X-M(X))^k и обозначается: μ_k=(X-M(X))^k

Следствия:

1. Центральный момент первого порядка равен нулю:

μ₁=(X-M(X))¹=M(X)-M(M(X))=M(X)-M(X)=0

2. Центральный момент второго порядка равен дисперсии:

μ₂=(X-M(X))²=D(X)

D(X)=M(X²)-(M(X))²=ν₂-ν₁²

Характеристики формы распределения:

Одно из характеристик служит коэфициет ассиметрии β₁: