Связь между декартовыми и полярными координатами
Связь между декартовыми и полярными координатами
Пару полярных координат  и
и 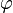 можно перевести в Декартовы координаты
можно перевести в Декартовы координаты 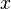 и
и 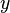 путём применения тригонометрических функций синуса и косинуса:
путём применения тригонометрических функций синуса и косинуса:
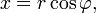
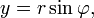
в то время как две декартовы координаты 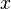 и
и 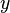 могут быть переведены в полярную координату
могут быть переведены в полярную координату  :
:
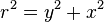 (по теореме Пифагора).
(по теореме Пифагора).
Для определения угловой координаты 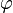 следует принять во внимание два следующие соображения:
следует принять во внимание два следующие соображения:
- Для
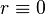 ,
, 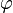 может быть произвольным действительным числом.
может быть произвольным действительным числом. - Для
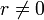 , чтобы получить уникальное значение
, чтобы получить уникальное значение 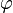 , следует ограничиться интервалом в
, следует ограничиться интервалом в 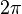 . Обычно выбирают интервал
. Обычно выбирают интервал 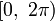 или
или 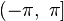 .
.
Для вычисления  в интервале
в интервале  , можно воспользоваться такими уравнениями (
, можно воспользоваться такими уравнениями (  обозначает обратную функцию к тангенсу):
обозначает обратную функцию к тангенсу):
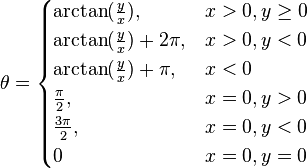
Для вычисления  в интервале
в интервале 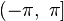 , можно воспользоваться такими уравнениями:[14]
, можно воспользоваться такими уравнениями:[14]
Учитывая, что для вычисления полярного угла не достаточно знать отношение 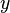 к
к 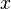 , а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты
, а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты 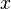 .
.
Нормированные векторы
Вектор 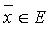 называется нормированным или единичным, если
называется нормированным или единичным, если 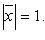
Если 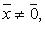 то соответствующими этому вектору нормированными векторами будут
то соответствующими этому вектору нормированными векторами будут 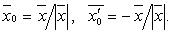
7) Понятие функции одной переменной
Рассмотрим два числовых множества X и Y. Правило f, по которому каждому числу хI Х ставится в соответствие единственное число yI Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y.
Таким образом, задать функцию, значит задать три объекта:
1) множество Х (область определения функции);
2) множество Y (область значений функции);
3) правило соответствия f (сама функция).
Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x3. В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y, пишут y = f(x). Здесь "х" называют независимой переменной или аргументом, а "y" -зависимой переменной (т.к. выражение типа x3 само по себе не имеет определенного числового значения пока не указано значение х) или функцией от х. О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у. Например, если х=2, то функция f(x) =x3 принимает значение у= f(2) =23 =8.
Способы задания функции одной переменной
Существуют несколько способов задания функции.
Аналитический способ. Функция f задается в виде формулы y=f(x). Например, y=3cos(x)+2x2. Этот способ является преобладающим в математических исследованиях и подробно рассматривается в классическом курсе математики. В географических исследованиях соответствие между переменными величинами x и y не всегда удается записать в виде формулы. Во многих случаях формула бывает неизвестна. Тогда для выражения функциональной зависимости используются другие способы.
Графический способ. На метеорологических станциях можно наблюдать работу приборов-самописцев, регистрирующих величины атмосферного давления, температуры воздуха, его влажности в любой момент времени суток. По полученному графику можно определить значения указанных величин в любой момент времени. Графиком функции y=f(x) называется множество всех точек плоскости с координатами (x, f(x)). График содержит всю информацию о функции. Имея перед собой график, мы как бы "видим функцию".
Табличный способ. Этот способ является наиболее простым. В одной строке таблицы записываются все значения аргумента (числа), а в другой – значения f(x), соответствующие каждому х. Например, зависимость температуры воздуха (Т) от времени суток (t) в определенный день можно представить таблицей.
| t | ||||||||||||
| T,0С |
Степенные функции:
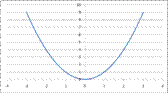
Функция вида у(х)=хn, где n – число Î R, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).
Степенная функция у=х²
1. D(x)=R – функция определена на все числовой оси;
2. E(y)=[0;∞) - функция принимает положительные значения на всей области определения;
3. При х=0 у=0 - функция проходит через начало координат O(0;0).
4. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).
5. Функция является четной (симметрична относительно оси Оу).
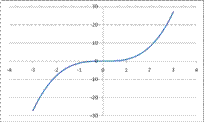
Степенная функция у=х³
1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:
2. D(x)=R – функция определена на все числовой оси;
3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;
4. При х=0 у=0 – функция проходит через начало координат O(0;0).
5. Функция возрастает на всей области определения.
6. Функция является нечетной (симметрична относительно начала координат).
Степенная функция с целым отрицательным показателем:
Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:
1. D(x)=(-∞;0)U(0;∞) для любого n;
2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;
3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.
4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.
5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.
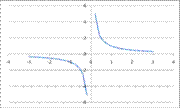
График функции 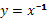 , на интервале x Î [-3;3]
, на интервале x Î [-3;3]
Степенная функция с дробным показателем
Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка)
1. D(x) Î R, если n – нечетное число и D(x)=[0;∞), если n – четное число ;
2. E(y) Î (-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число;
3. Функция возрастает на всей области определения для любого числа n.
4. Функция проходит через начало координат в любом случае.
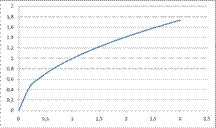
График функции 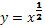 , на интервале x Î [0;3]
, на интервале x Î [0;3]
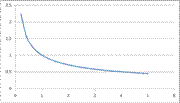
График функции 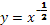 , на интервале x Î [0;5]
, на интервале x Î [0;5]
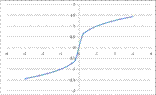
График функции 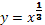 , на интервале x Î [-3;3]
, на интервале x Î [-3;3]
Логарифмические функции:
Логарифмическая функция у = loga x обладает следующими свойствами :
1. Область определения D(x) Î (0; + ∞).
2. Область значений E(y) Î ( - ∞; + ∞)
3. Функция ни четная, ни нечетная (общего вида).
4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.
График функции у = loga x может быть получен из графика функции у = ах с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 - для 0 < a < 1.
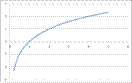
График функции 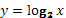 ; на интервале x Î [0;5]
; на интервале x Î [0;5]
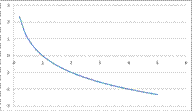
График функции 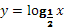 ; на интервале x Î [0;5]
; на интервале x Î [0;5]
Тригонометрические функции:
Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.
Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.
Функция y = sin (х).
1. Область определения D(x) Î R.
2. Область значений E(y) Î [ - 1; 1].
3. Функция периодическая; основной период равен 2π.
4. Функция нечетная .
5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.
График функции у = sin (х)

График функции 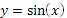 ; на интервале x Î [-2
; на интервале x Î [-2 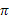 ;2
;2 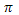 ]
]
Функция y = cos(х).
1. Область определения D(x) Î R.
2. Область значений E(y) Î [ - 1; 1].
3. Функция периодическая с основным периодом 2π.
4. Функция четная.
5. Функция убывает на промежутках [2πn; π+ 2πn] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.
График функции у = соs (х)
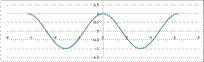
График функции 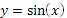 ; на интервале x Î [-2
; на интервале x Î [-2  ;2
;2  ]
]
Функция y = tg х.
1. Область определения: D(x) Ï π/2 + πk, kÎZ.
2. Область значений E(y) Î (- ∞; + ∞)
3. π- основной период функции.
4. Функция нечетная.
5. Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).
График функции у = tg х

График функции 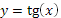 ; на интервале x Î (-
; на интервале x Î (-  ;
; 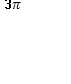 )
)
Функция y = ctg х.
1. Область определения функции: D(x) Ï xπ/2 +πk, kÎZ.
2. Область значений функции E(y) Î (- ∞; + ∞).
3. Функция периодическая с основным периодом π.
4. Функция нечетная.
5. Функция у = ctg х убывает на промежутках (πn;π+πn).
График функции у = ctg х
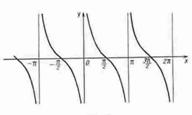
График функции 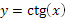 ; на интервале x Î (-𝜋;)
; на интервале x Î (-𝜋;)
Обратные тригонометрические функции:
Функции y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х) называют обратными тригонометрическими функциями.
Функция
y
=
arcsin
(
x
):
Свойства функции y = arcsin (x):
1. Область определения D(x)Î[−1;1]
2. Область значения E(y)Î [−π/2;π/2]
3. y=arcsin(x)- непрерывная строговозрастающая функция на D
5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x
6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х)
График функции y = arcsin (x)
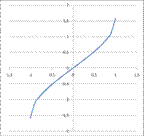
График функции 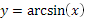 ; на интервале x Î [-
; на интервале x Î [-  ;]
;]
Функция
y
=
arccos
(
x
):
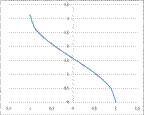
Свойства функции y = arccos (x):
1. Область определения D(x)Î[−1;1]
2. Область значения E(y)Î [0;π]
3. y=arccos(x)- непрерывная строговозрастающая функция на D
5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x
6. y=arccos(x) функция общего вида
График функции y = arccos (x)
8) Числовая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Пусть множество 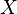 — это либо множество вещественных чисел
— это либо множество вещественных чисел 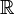 , либо множество комплексных чисел
, либо множество комплексных чисел 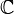 . Тогда последовательность
. Тогда последовательность 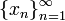 элементов множества
элементов множества 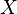 называется числовой последовательностью.
называется числовой последовательностью.
Примеры
- Функция
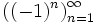 является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид 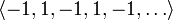 .
. - Функция
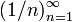 является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид 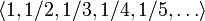 .
. - Функция, сопоставляющая каждому натуральному числу
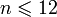 одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида
одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида 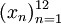 . В частности, пятым членом
. В частности, пятым членом 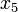 этой последовательности является слово «май».
этой последовательности является слово «май».
Предел последовательности
Основная статья: Предел последовательности
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
9) Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.
Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция оказывается непрерывной (в данной точке).
Предел фу́нкции — одно из основных понятий математического анализа.
10) Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Определения
[править]ε-δ определение
Пусть 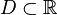 и
и 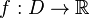 .
.
Функция 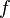 непрерывна в точке
непрерывна в точке 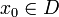 , если для любого
, если для любого 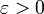 существует
существует 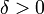 такое, что для любого
такое, что для любого
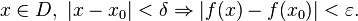
Функция 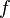 непрерывна на множестве
непрерывна на множестве 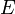 , если она непрерывна в каждой точке данного множества.
, если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция 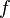 класса
класса 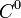 и пишут:
и пишут: 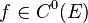 или, подробнее,
или, подробнее, 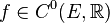 .
.
[править]Комментарии
· Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция 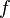 непрерывна в точке
непрерывна в точке 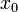 , предельной для множества
, предельной для множества 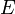 , если
, если 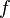 имеет предел в точке
имеет предел в точке 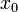 , и этот предел совпадает со значением функции
, и этот предел совпадает со значением функции 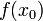 .
.
· Функция непрерывна в точке, если её колебание в данной точке равно нулю.
[править]Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если 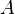 — значение функции
— значение функции 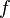 в точке
в точке 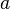 , то предел такой функции (если он существует) не совпадает с
, то предел такой функции (если он существует) не совпадает с 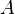 . На языке окрестностей условие разрывности функции
. На языке окрестностей условие разрывности функции 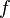 в точке
в точке 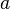 получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки
получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки 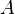 области значений функции
области значений функции 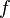 , что как бы мы близко не подходили к точке
, что как бы мы близко не подходили к точке 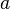 области определения функции
области определения функции 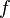 , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки
, всегда найдутся такие точки, чьи образы будут за пределами окрестности точки 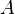 .
.
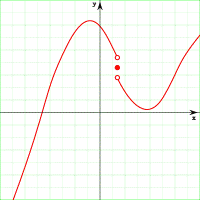
[править]Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
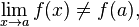
тогда точка 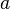 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции 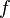 (в комплексном анализе — устранимая особая точка).
(в комплексном анализе — устранимая особая точка).
Если «поправить» функцию 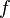 в точке устранимого разрыва и положить
в точке устранимого разрыва и положить 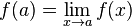 , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
, то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
[править]Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
· если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
· если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
[править]Свойства
[править]Локальные
· Функция, непрерывная в точке 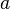 , является ограниченной в некоторой окрестности этой точки.
, является ограниченной в некоторой окрестности этой точки.
· Если функция 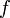 непрерывна в точке
непрерывна в точке 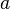 и
и 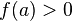 (или
(или 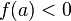 ), то
), то 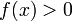 (или
(или 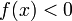 ) для всех
) для всех 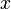 , достаточно близких к
, достаточно близких к 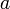 .
.
· Если функции 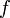 и
и 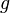 непрерывны в точке
непрерывны в точке 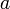 , то функции
, то функции 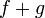 и
и 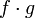 тоже непрерывны в точке
тоже непрерывны в точке 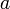 .
.
· Если функции 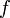 и
и 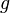 непрерывны в точке
непрерывны в точке 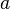 и при этом
и при этом 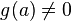 , то функция
, то функция 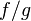 тоже непрерывна в точке
тоже непрерывна в точке 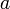 .
.
· Если функция 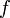 непрерывна в точке
непрерывна в точке 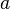 и функция
и функция 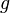 непрерывна в точке
непрерывна в точке 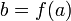 , то их композиция
, то их композиция 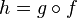 непрерывна в точке
непрерывна в точке 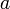 .
.
[править]Глобальные
· Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
· Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
· Областью значений функции 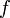 , непрерывной на отрезке
, непрерывной на отрезке 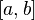 , является отрезок
, является отрезок 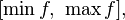 где минимум и максимум берутся по отрезку
где минимум и максимум берутся по отрезку 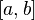 .
.
· Если функция 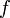 непрерывна на отрезке
непрерывна на отрезке 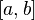 и
и 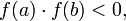 то существует точка
то существует точка 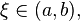 в которой
в которой 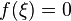 .
.
· Если функция 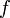 непрерывна на отрезке
непрерывна на отрезке 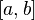 и число
и число 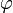 удовлетворяет неравенству
удовлетворяет неравенству 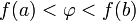 или неравенству
или неравенству 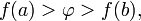 то существует точка
то существует точка 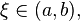 в которой
в которой  .
.
· Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
· Монотонная функция на отрезке 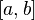 непрерывна в том и только в том случае, когда область ее значений является отрезком с концами
непрерывна в том и только в том случае, когда область ее значений является отрезком с концами 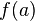 и
и 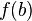 .
.
· Если функции 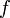 и
и 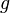 непрерывны на отрезке
непрерывны на отрезке 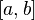 , причем
, причем 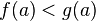 и
и 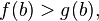 то существует точка
то существует точка 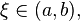 в которой
в которой 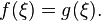 Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
11) Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Бесконечно малая величина
Последовательность 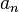 называется бесконечно малой, если
называется бесконечно малой, если 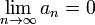 . Например, последовательность чисел
. Например, последовательность чисел 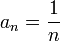 — бесконечно малая.
— бесконечно малая.
Функция называется бесконечно малой в окрестности точки 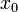 , если
, если 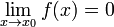 .
.
Функция называется бесконечно малой на бесконечности, если 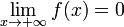 либо
либо 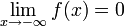 .
.
Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если 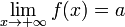 , то
, то 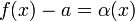 ,
, 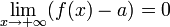 .
.
[править]Бесконечно большая величина
Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция 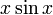 , неограниченная с обеих сторон, не является бесконечно большой при
, неограниченная с обеих сторон, не является бесконечно большой при 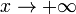 .
.
Последовательность 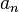 называется бесконечно большой, если
называется бесконечно большой, если 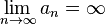 .
.
Функция называется бесконечно большой в окрестности точки 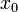 , если
, если 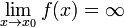 .
.
Функция называется бесконечно большой на бесконечности, если 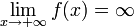 либо
либо 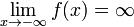 .
.
[править]Свойства бесконечно малых
· Сумма конечного числа бесконечно малых — бесконечно малая.
· Произведение бесконечно малых — бесконечно малая.
· Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
· Если 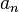 — бесконечно малая последовательность, сохраняющая знак, то
— бесконечно малая последовательность, сохраняющая знак, то 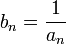 — бесконечно большая последовательность.
— бесконечно большая последовательность.
12) Рассмотрим теоремы о правилах предельного перехода. Т.1: Предел постоянной равен самой постоянной Доказательство следует из определения предела функции, так как 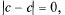 если с = const.
если с = const.
Т.2: (о связи функции с ее пределом). Для того чтобы 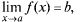 необходимо и достаточно выполнение равенства
необходимо и достаточно выполнение равенства 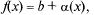 где
где 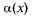 — б.м. при х
— б.м. при х 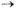 а
а 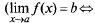
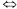
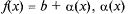
— б.м., х 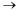 а)
а)
Запишем цепочку равносильных утверждений, следующих из определения предела функции и определения б.м.:
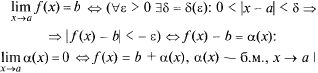
Т.3: Предел суммы конечного числа функций, имеющих пределы при х  а, равен сумме их пределов
а, равен сумме их пределов
Пусть 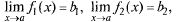 тогда по теореме 2 име-
тогда по теореме 2 име-
ем 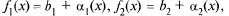 где
где 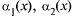 — б.м. при
— б.м. при
х 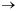 а, следовательно,
а, следовательно, 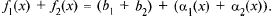 Используя лемму 1 о б.м., заключаем, что
Используя лемму 1 о б.м., заключаем, что 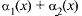 — б.м. при
— б.м. при
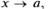 и по теореме 2 получаем равенство
и по теореме 2 получаем равенство 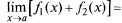 b1 + b2
b1 + b2
Т.4: Предел произведения конечного числа функций, имеющих пределы при х 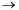 а, равен произведению пределов Методика доказательства аналогична доказательству Т.3. Следствие. Постоянный множитель можно выносить за знак предела.
а, равен произведению пределов Методика доказательства аналогична доказательству Т.3. Следствие. Постоянный множитель можно выносить за знак предела.
Т.5: Предел отношения двух функций, имеющих пределы при х 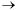 а, равен отношению их пределов (если предел знаменателя не нуль), т.е.
а, равен отношению их пределов (если предел знаменателя не нуль), т.е.
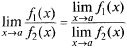
Пусть 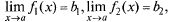 тогда, используя Т.2, аналогично доказательству Т.3 запишем
тогда, используя Т.2, аналогично доказательству Т.3 запишем
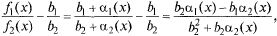
где 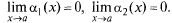 Числитель последней дроби по леммам о б.м. является б.м. Покажем, что
Числитель последней дроби по леммам о б.м. является б.м. Покажем, что 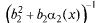 является функцией ограниченной, тогда дробь по лемме 2 о б.м. является б.м., и по Т.2:
является функцией ограниченной, тогда дробь по лемме 2 о б.м. является б.м., и по Т.2: 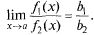
Имеем в некоторой  окрестности т. а для любого
окрестности т. а для любого  > 0 вследствие справедливости
> 0 вследствие справедливости 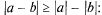
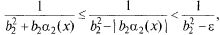
т.е. ограниченность 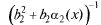 доказана
доказана
13) Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Пусть в некоторой окрестности точки 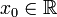 определена функция
определена функция 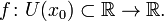 Производной функции называется такое число
Производной функции называется такое число 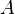 , что функцию в окрестности
, что функцию в окрестности 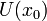 можно представить в виде
можно представить в виде
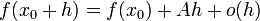
если 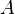 существует.
существует.
[править]Определение производной функции через предел
Пусть в некоторой окрестности точки 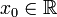 определена функция
определена функция 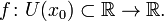 Производной функции
Производной функции 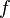 в точке
в точке 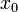 называется предел, если он существует,
называется предел, если он существует,
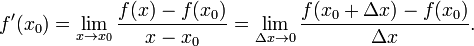
[править]Общепринятые обозначения производной функции 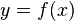 в точке
в точке 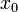
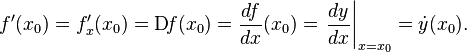
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).
14) Физический Изменения проявлений каких-либо свойств или состояний смысл объектов реального мира мы обычно связываем с течением реального ("физического") времени, При этом, мы легко выделяем направленность подобных изменений ("возрастание", "убывание") и их количественную значимость, отнесенную к единице измерения временного интервала наблюдения (т. е., "скорость" изменений).
Именно указанная особенность отражения в нашем сознании восприятия изменений окружающего мира позволяет рассматривать численное значение производной y'(x) к<
