Условия параллельности и перпендикулярности в пространстве.

Условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если: 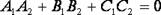. Плоскости параллельны, векторы нормалей коллинеарны: 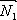|| 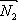.Это условие выполняется, если: A₁\A₂=B₁\B₂=C₁\C₂.

Условия параллельности и перпендикулярности прямых в пространстве. Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.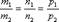

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю. .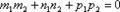

Условия параллельности и перпендикулярности прямой и плоскости в пространстве. Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю. .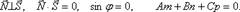

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю. .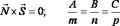

Вопрос №29

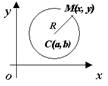Окружность. Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности.

Пусть центр окружности находится в точке С(а, b). Т.к. окружность есть множество точек М(х, у), находящихся на расстоянии R (радиус окружности) от центра С(а, b), то 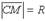, то есть 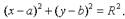(1). Уравнение (1) и есть уравнение окружности с центром в точке С(а, b) и радиусом R. Если центр окружности находится в начале координат, то ее уравнение примет вид: .

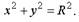Эллипс. Эллипс есть геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).

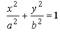- каноническое уравнение эллипса.

Форма. Из канонического уравнения понятно, что оси координат Ох и Оу являются осями симметрии эллипса и, следовательно, начало координат является центром симметрии эллипса.

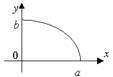Рассмотрим часть эллипса, расположенную в первой четверти, для которой можем записать каноническоеуравнение в виде: .

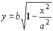Отсюда видно, что если x = 0, то y = b и, далее, с ростом х значения у убывают. Когда x = a, то y = 0.

Числа а и b называют полуосями эллипса.

Учитывая симметрию эллипса относительно осей координат, можем построить полный эллипс.

Если изменяется величина с, то меняется форма эллипса, а именно: если 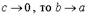и при c = 0 эллипс становится окружностью с уравнением 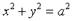. Т.о., окружность есть частный случай эллипса, когда полуоси эллипса равны между собой.

Если же с->a, то 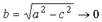, т.е. эллипс сжимается вдоль оси Оу. Величина c\a может служить числовой характеристикой сжатия эллипса.

Число 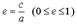называют эксцентриситетом эллипса. Две прямые 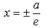называются директрисами эллипса. Точки пересечения эллипса с осями симметрии 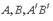называют вершинами эллипса.

Вопрос №30

Гипербола есть геометрическое место точек, абсолютное значение разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами.

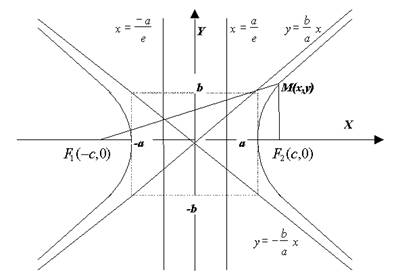
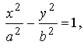- каноническое уравнениегиперболы.

Число а называют действительной полуосью Число а называют действительной полуосью гиперболы, число b - мнимой полуосью.

Кривая состоит из двух отдельных частей - ветвей гиперболы, лежащих в областях .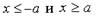

Можно показать, что при 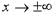ветви гиперболы неограниченно приближаются к прямым 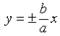, не пересекая этих прямых.

Эти две прямые называются асимптотами гиперболы.

Число 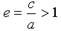, количественно характеризующее сжатие ветвей гиперболы, называют эксцентриситетом гиперболы.

Точки пересечения гиперболы с действительной осью называются вершинами гиперболы.

Две прямые 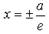называют директрисами гиперболы.

Директрисы гиперболы параллельны оси Оу и пересекают ось Ох между вершинами гиперболы.

Вопрос №31

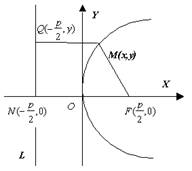Парабола есть геометрическое место точек, для каждой из которых расстояние от некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой (директриса не проходит через фокус).

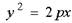- каноническое уравнение параболы.

Значение р называют параметром параболы.