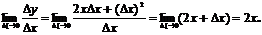Свойства функций, непрерывных в точке
1. Если функции 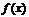 и
и 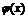 непрерывны в точке
непрерывны в точке 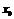 , то их сумма
, то их сумма 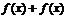 , произведение
, произведение 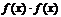 и частное
и частное 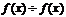 (при условии
(при условии 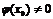 ) являются функциями, непрерывными в точке
) являются функциями, непрерывными в точке 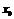 .
.
2. Если функция 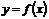 непрерывна в точке
непрерывна в точке 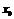 и
и 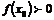 , то существует такая окрестность точки
, то существует такая окрестность точки 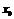 , в которой
, в которой 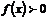 .
.
Доказательство этого свойства основывается на том, что при малых приращениях аргумента 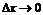 можно получить как угодно малое приращение функции
можно получить как угодно малое приращение функции 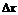 в окрестностях
в окрестностях 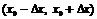 не изменится.
не изменится.
3. Если функция 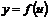 непрерывна в точке
непрерывна в точке 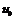 , а функция
, а функция 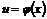 непрерывна в точке
непрерывна в точке 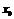 , то сложная функция
, то сложная функция 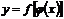 непрерывна в точке
непрерывна в точке 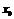 . Доказательство состоит в том, что малому приращению аргумента
. Доказательство состоит в том, что малому приращению аргумента 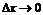 соответствует как угодно малое приращение
соответствует как угодно малое приращение 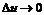 , приводящее в свою очередь к непрерывности функции
, приводящее в свою очередь к непрерывности функции 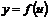 к как угодномалому приращению
к как угодномалому приращению 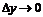 .
.
Свойство можно записать: 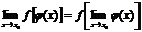 ,
,
Т.е. под знаком непрерывной функции можно переходить к пределу.
Определение.Функция 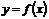 называется непрерывнойна промежутке
называется непрерывнойна промежутке 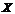 , если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.
, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.
Точки разрыва функции
Определение. Если в какой-нибудь точке 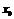 для функции
для функции 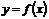 не выполняется по крайней мере одно из условий непрерывности, то эта точка называется точкой разрыва функции.
не выполняется по крайней мере одно из условий непрерывности, то эта точка называется точкой разрыва функции.
Причем: 1) Если существуют конечные односторонние пределы функции, неравные друг другу: 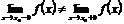 , то точка
, то точка 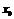 - точка разрыва I рода.
- точка разрыва I рода.
2) Если хотя бы один из односторонних пределов функции 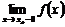 или
или 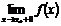 равен бесконечности или не существует, то точка
равен бесконечности или не существует, то точка 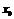 - точка разрыва II рода.
- точка разрыва II рода.
Свойства функций, непрерывных на отрезке
1. Если функция 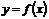 непрерывна на отрезке
непрерывна на отрезке 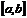 , то она ограничена на этом отрезке. (рис. 1.1)
, то она ограничена на этом отрезке. (рис. 1.1)
2. Если функция 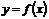 непрерывна на отрезке
непрерывна на отрезке 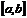 , то она достигает на этом отрезке наименьшего значения
, то она достигает на этом отрезке наименьшего значения 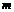 и наибольшего значения
и наибольшего значения 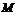 (теорема Вейерштрасса). (рис. 1.2)
(теорема Вейерштрасса). (рис. 1.2)
 3. Если функция
3. Если функция 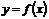 непрерывна на отрезке
непрерывна на отрезке 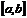 и значения ее на концах отрезка
и значения ее на концах отрезка 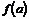 и
и 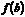 имеют противоположные знаки, то внутри отрезка найдется точка
имеют противоположные знаки, то внутри отрезка найдется точка 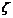 такая, что
такая, что 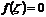 . (Теорема Больцано-Коши.)
. (Теорема Больцано-Коши.)
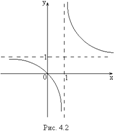
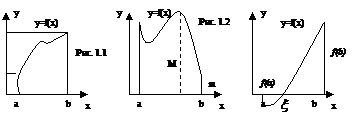 Пример.Исследовать на непрерывность и найти точки разрыва функции
Пример.Исследовать на непрерывность и найти точки разрыва функции 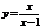 . Установить характер разрыва.
. Установить характер разрыва.
Решение. При 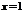 функция не определена, следовательно, функция в точке
функция не определена, следовательно, функция в точке 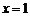 терпит разрыв:
терпит разрыв: 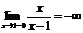 , а
, а 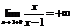 . Так как односторонние пределы бесконечны, то
. Так как односторонние пределы бесконечны, то 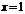 - точка разрыва второго рода.
- точка разрыва второго рода.
Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке.
Определение производной
Пусть на некотором промежутке Х определена функция y=f(x). Возьмем любую точку 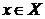 . Зададим аргументу х произвольное приращение ∆х ≠ 0 такое, что точка х+∆х также будет принадлежать Х. Функция получит приращение ∆у= f(x+∆х)− f(x).
. Зададим аргументу х произвольное приращение ∆х ≠ 0 такое, что точка х+∆х также будет принадлежать Х. Функция получит приращение ∆у= f(x+∆х)− f(x).
Определение. Производной функции y=f(x) в точке х называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует).
Для обозначения производной функции y=f(x) в точке х используются символы у′(х) или f′(x).
Итак, по определению, 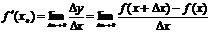 .
.
Если для некоторого значения х0 выполняется условие
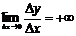 или
или 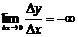 ,
,
т.е. пределы равны бесконечности, то говорят, что в точке х0 функция имеет бесконечную производную.
Если функция y=f(x)имеет конечную производную в каждой точке 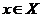 , то производную f′(x) можно рассматривать как функцию х, также определенную на Х. Нахождение производной функции называется дифференцированием функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
, то производную f′(x) можно рассматривать как функцию х, также определенную на Х. Нахождение производной функции называется дифференцированием функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
Задача о касательной
Пусть на плоскости 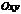 дана непрерывная функция
дана непрерывная функция 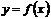 и необходимо найти уравнение касательной к этой кривой в точке
и необходимо найти уравнение касательной к этой кривой в точке 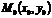 .
.
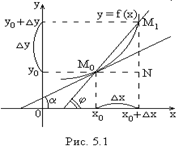 | Уравнение прямой по точке 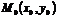 , принадлежащей этой прямой, и угловому коэффициенту имеет вид: , принадлежащей этой прямой, и угловому коэффициенту имеет вид: 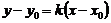 , где , где 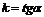 , ( , ( 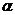 - угол наклона прямой). Из - угол наклона прямой). Из 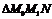 (рис.5.1) найдем тангенс угла наклона секущей (рис.5.1) найдем тангенс угла наклона секущей 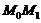 : : 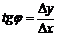 . Если точку . Если точку 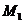 приближать к точке приближать к точке 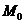 , то угол , то угол 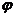 будет стремиться к углу будет стремиться к углу 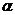 , т.е. при , т.е. при 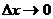 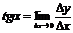 . Следовательно, . Следовательно, 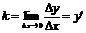 . . |
Из задачи о касательной следует геометрический смысл производной: производная f′(x0) есть угловой коэффициент(тангенс угла наклона) касательной, проведенной к кривой у=f′(x) в точке х0, т.е. k= f′(x0).
Следовательно, уравнение касательной к кривой y=f(x) в точке х0 примет вид
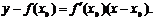
Пример. Найти производную функции f(x)=х2.
Решение. Придавая аргументу х приращение ∆х, найдем соответствующее приращение функции:
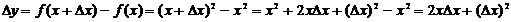
Составим отношение:
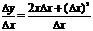
Найдем предел этого отношения при ∆х → 0: