Свойства бесконечно малых функций.
1. Алгебраическая сумма конечного числа БМ  Ф есть БМФ при
Ф есть БМФ при  .
.
2. Произведение БМ  Ф на ограниченную в некоторой окрестности точки
Ф на ограниченную в некоторой окрестности точки 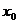 функцию (в т.ч. на постоянную, на другую БМ) есть БМ
функцию (в т.ч. на постоянную, на другую БМ) есть БМ  Ф.
Ф.
3. Частное от деления БМ  Ф на функцию, предел которой отличен от нуля, есть БМ
Ф на функцию, предел которой отличен от нуля, есть БМ  Ф.
Ф.
Замечание. Свойство 3 не рассматривает предел отношения двух БМ  Ф из-за его неопределенности: он может быть равен как конечному числу, так и
Ф из-за его неопределенности: он может быть равен как конечному числу, так и 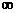 .
.
Докажем, например, свойство 1.
Пусть 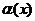 и
и 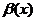 есть БМ
есть БМ  Ф. Докажем, что функция
Ф. Докажем, что функция 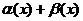 также есть БМ
также есть БМ  Ф.
Ф.
По условию для любого 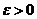 , а значит, и для
, а значит, и для 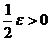 найдутся такие числа
найдутся такие числа 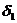 и
и 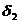 , что
, что 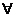
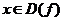 :
:
если 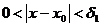 , то
, то
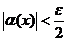 (1)
(1)
если 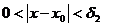 , то
, то
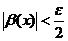 (2)
(2)
Если в качестве 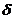 взять минимальное из
взять минимальное из 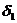 и
и 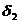 , т.е.
, т.е. 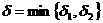 , то для всех х, удовлетворяющих условию
, то для всех х, удовлетворяющих условию 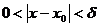 будут верны оба неравенства (1) и (2). Складывая их почленно, получим:
будут верны оба неравенства (1) и (2). Складывая их почленно, получим:
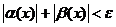 .
.
Используя первое неравенство треугольника, перейдем к более сильному неравенству:
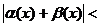
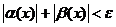 .
.
Итак, 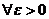 мы нашли
мы нашли 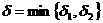 , такое, что при всех
, такое, что при всех 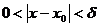 выполняется неравенство
выполняется неравенство 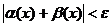 . Это и означает, что функция
. Это и означает, что функция 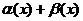 есть БМ
есть БМ  Ф. ▲
Ф. ▲
Свойства бесконечно больших функций.
1. Произведение ББ  Ф на функцию, предел которой отличен от 0, есть ББ
Ф на функцию, предел которой отличен от 0, есть ББ  Ф.
Ф.
2. Сумма ББ  Ф и ограниченной функции есть ББ
Ф и ограниченной функции есть ББ  Ф.
Ф.
3. Сумма ББ  Ф одного знака есть ББ
Ф одного знака есть ББ  Ф того же знака.
Ф того же знака.
4. Частное от деления ББ  Ф на функцию, имеющую конечный предел, есть ББ
Ф на функцию, имеющую конечный предел, есть ББ  Ф.
Ф.
5.Теорема о связи предела и бесконечно малой функции (с док.). Теорема о связи бесконечно малой и бесконечно большой функций (без док.). Сравнение бесконечно малых функций.
Теорема 1. (о связи предела и бесконечно малой функции). Если функция
y=f(x) имеет предел 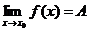 , то разность между функцией и значением ее предела есть бесконечно малая при
, то разность между функцией и значением ее предела есть бесконечно малая при  .
.
Док-во. Имеем:
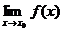 =А
=А 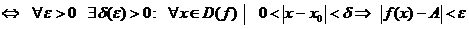 .
.
Надо доказать, что 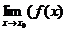 -А)=0, т.е.
-А)=0, т.е.
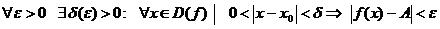 . Очевидно, что это условие выполнено. ▲
. Очевидно, что это условие выполнено. ▲
Следствие. Если функция y=f(x) имеет предел 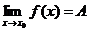 , то ее можно представить в виде суммы этого числа А и бесконечно малой при
, то ее можно представить в виде суммы этого числа А и бесконечно малой при  функции
функции 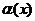 :
: 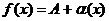 .
.
Теорема 2 ( о связи БМ и ББ функций). Если 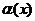 есть БМ
есть БМ  Ф, и
Ф, и 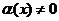 в некоторой окрестности точки
в некоторой окрестности точки 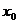 , то функция
, то функция 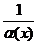 есть ББ
есть ББ  Ф. Если
Ф. Если 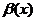 есть ББ
есть ББ  Ф, то функция
Ф, то функция 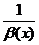 есть БМ
есть БМ  Ф.
Ф.
Сравнение бесконечно малых функций
Пусть 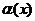 и
и 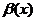 - БМ
- БМ  Ф. Предположим, что существует предел их отношения, равный некоторому значению А (собств. или несобств.), т.е.
Ф. Предположим, что существует предел их отношения, равный некоторому значению А (собств. или несобств.), т.е.
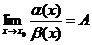 . Тогда если:
. Тогда если:
1) А – число, не равное 0 или 1, то функции 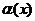 и
и 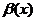 называются БМ одинакового порядка.
называются БМ одинакового порядка.
2) А=0, то функция 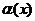 называется БМ более высокого порядка малости, чем
называется БМ более высокого порядка малости, чем 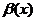 и обозначают:
и обозначают: 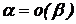 (о малое).
(о малое).
Пример:
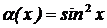 ,
, 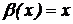 - БМ при х→0,
- БМ при х→0,
3) А= 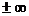 , то функция
, то функция 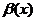 называется БМ более высокого порядка малости, чем
называется БМ более высокого порядка малости, чем 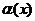 .
.
4) А =1, то функции 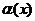 и
и 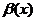 называются эквивалентными БМ
называются эквивалентными БМ  , обозначается:
, обозначается: 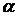 ~
~ 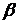 .
.
Свойства эквивалентных БМ
1. 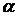 ~
~ 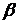 ↔
↔ 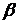 ~
~ 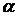 (рефлексивность)
(рефлексивность)
2. 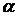 ~
~ 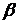 ,
, 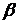 ~
~ 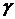 ↔
↔ 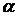 ~
~ 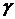 (транзитивность)
(транзитивность)
3. 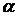 ~
~ 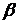 →
→ 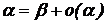 эквивалентные БМ отличаются друг от друга на БМ высшего порядка малости.
эквивалентные БМ отличаются друг от друга на БМ высшего порядка малости.
4. Под знаком предела в отношении или произведении БМ можно заменять эквивалентными БМ.
6.Основные теоремы о пределах. Необходимые условия существования конечного предела функции.
Теорема (о предельном переходе в равенствах). Если в некоторой окрестности точки 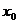 значения функций f(x) и g(x) совпадают, то их пределы в этой точке равны:
значения функций f(x) и g(x) совпадают, то их пределы в этой точке равны:
f(x)=g(x) => 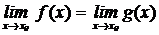 .
.
Теорема ( о предельном переходе в неравенствах). Если в некоторой окрестности точки 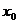 выполняется неравенство f(x)≤ g(x), то верно и неравенство:
выполняется неравенство f(x)≤ g(x), то верно и неравенство: 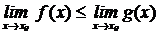 .
.
Теорема. Предел постоянной равен самой постоянной: 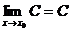 .
.
Док-во. Проводится на основании определения, где в качестве 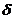 можно взять любое положительное число. Тогда при
можно взять любое положительное число. Тогда при  .▲
.▲
Теорема (о единственности предела). Функция не может иметь более одного предела в данной точке.
Док-во. Предположим противное. Пусть 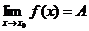 и
и 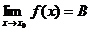 ,
, 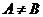 . Тогда по теореме о связи предела и БМ:
. Тогда по теореме о связи предела и БМ:
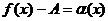 - БМ при
- БМ при  ,
,
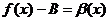 - БМ при
- БМ при  . Вычитая эти равенства, получим:
. Вычитая эти равенства, получим:
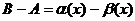 .
.
На основании свойства 1 БМФ это есть БМ. Переходя в этом равенстве к пределу, получим:
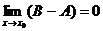 ,
,
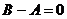 .
.
Получено противоречие, доказывающее теорему.▲
