Вопрос 16. Частные производные и дифференциалы функции двух переменных высших порядков.

1.Частные производные:

Пусть частная производная∂∂uxx xi( , . . . , )1 m функции u=f(x1,...,xm) существует в ка-

ждой точке некоторого множества { } M , т.е. представляет собой функцию переменных x1,

..., xm. Если эта функция имеет частную производную по переменной хk в некоторой точке

М0, то она называется второй частной производной функции f(x1, ..., xm) по переменным xi

и xk и обозначается ∂²u\∂xi∂xk , f’’ xi,xk.

Совершенно аналогично определяются и последующие частные производные

функции f.

Таким образом,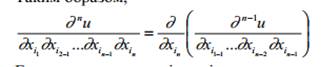

Если не все индексы i1, ..., in совпадают между собой, то частная производная назы-

вается смешанной.

Вычисляются частные производные по тем же правилам, что и обыкновенные про-

изводные. Необходимо только следить при каждом дифференцировании, чтобы все пере-

менные, кроме одной, считались постоянными.

Теорема. Пусть функция u=f(x1, ..., xm) определена в открытой m – мерной области

D и имеет в этой области всевозможные частные производные n-го порядка, причем все

эти производные непрерывны в D. Тогда значение любой к-ой смешанной производной не

зависит от того порядка, в котором производятся последовательные дифференцирования.

В подавляющем большинстве конкретных задач условия теоремы выполняются, и сме-

шанную производную можно вычислять, не обращая внимания на порядок последова-

тельных дифференцирований.

2.Дифференциалы высших порядков:

Пусть в некоторой области задана дифференцируемая функция u=f(x1, ..., xm), тогда

в каждой точке этой области определен дифференциал

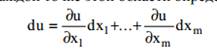
Здесь частные производные являются функциями от x1, ..., xm. Если существуют

непрерывные частные производные второго порядка для u, то du будет иметь непрерыв-

ные частные производные по x1, ..., xm. Будем считать, что dx1, ..., dxm постоянны, тогда

можно определить дифференциал от первого дифференциала:

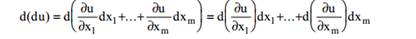
При вычислении дифференциалов от частных производных будем считать, что dx1,

..., dxm имеют те же самые значения, что и в исходном дифференциале du.

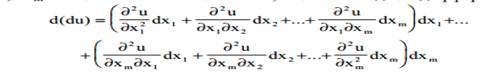
Полученное таким образом выражение мы назовем дифференциалом второго по-

рядка функции u

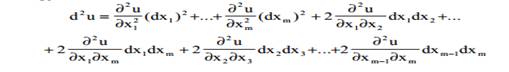
Точно так же мы определим и последующие дифференциалы функции u с помощью равенства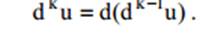

Вопрос 17. Локальный экстремум функции двух переменных, необходимые, достаточные условия его существования.

Локальный это тоже самое что и наименьшее и наибольшее значении функции.

Наибольшее или наименьшее знчение функции может достигаться как в точках экстремума, так и в точках на концах отрезка.

Для нахождения наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:

1) Найти производную функции

2) Найти критические точки функции, в которых производная равна нулю или не существует.

3) Найти значения функции в критических точках и на конфах отрезкаи выбрать из них наибольшее и наименьшее.